决策规则与策略

9.1.4　历史、决策规则与策略

从决策的过程能够看出马尔科夫决策过程的一条轨迹可以用相继的状态和行动组成。我们把到t时刻的一条轨迹记为

h_t＝（i₀，a₀，i₁，a₁，…，i_t-1，a_t-1，i_t）t≥0　　　　　（9.4）

称为从时刻0到时刻t的一条历史，其中i_k∈S和a_k∈A（i_k）分别表示决策时刻k时系统所处的状态和决策者采取的行动（k＝0，1，…，t-1），i_t∈S为系统当前所处的状态。全体到时刻t的历史为H_t。如果采用计划乘积的记号，有

H_t＝H_t-1×A×s＝（S×A）^t×S　　　　　（9.5）

如果t→∞，则H_∞为所有轨迹的集合。

一个决策规则描述了一个决策时刻系统在各个不同的状态上选取行动的规则。决策规则的范围比较广，从选取确定的某个行动，到根据历史的决策过程随机的选取行动。记N_＋＝｛1，2，…，｝为全体正整数的集合，N＝｛0，1，2，…，｝为全体非负数集合。我们给出决策规则的具体定义如下。

定义1 如果状态空间上的函数f满足：对每个i∈S，有f（i）∈A（i），即f：S→A（i），则称f为确定性决策规则，或称为决策函数或者马尔科夫决策函数。全体决策函数所组成的集合记作F。

如果状态空间上的概率分布函数π_t满足：对每个时刻t时刻的i∈S，π_t（·｜i）∈Dis（A（i））是A（i）上的一个概率分布，即满足π_t（a｜i）≥0且

那么称π_t为马尔科夫决策规则，这里t∈N是决策时刻。决策函数是马尔科夫决策规则的退化情形。

如果状态空间上的概率分布函数π_t满足：在t时刻的历史为h_t∈H_t的条件下，π_t（·｜h_t）∈Dis（A（i））是A（i）上的一个概率分布，即满足π_t（a｜h_t）≥0且

那么称π_t为一般决策规则，这里t∈N是决策时刻。马尔科夫决策规则是一般决策规则的退化情形。

注意：对于一般决策规则来讲，在不同的历史和下，尽管0和t两个时刻系统都处于相同的状态i₀和i_t，分布函数π_t与一般也不相同。

定义2 一个决策函数序列π＝（f₀，f₁，…），f_t∈F，t∈N称为（确定性）马尔科夫策略。其中f_t是决策时刻t的决策函数，不依赖于时刻t以前系统的历史，t∈N。全体马尔科夫策略所组成的集合记作称为马尔科夫策略类。

一个马尔科夫决策规则序列π＝（π₀，π₁，…）称为随机马尔科夫策略，其中π_t是决策时刻t的决策规则且不依赖于时刻t以前系统的历史，t∈N。全体随机马尔科夫策略所组成的集合记作Π_m，称为随机马尔科夫策略类。

定义3 一个决策规则序列π＝（π₀，π₁，…），如果时刻t的决策规则π_t不仅是随机的，而且依赖于系统的历史h_t，t∈N，这是最一般的策略。全体一般策略所组成的集合记作Π，称为策略空间。如果对一切t，π_t是依赖于系统的历史h_t的退化分布，则π称为决定性策略，全体决定性策略记为Π_d，称为决定性策略类。

从定义可以看出，一般的策略使用起来时是很不方便的，因为随着时间的推移，这种策略选取控制系统的行动时需要考虑到系统的整个发展历史。如果能找到比较简单的控制方式，那是求之不得的，因此我们对特殊的策略更感兴趣。

定义4 一个马尔科夫策略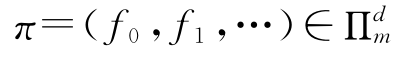，如果对每个t∈N，都有f_t≡f₀，则称它为（确定性）平稳策略，记作。全体平稳策略所组成的集合记作，并称为平稳策略类。在不引起混淆时，一个平稳策略f^∞有时也简记为f。

一个随机马尔科夫策略π＝（π₀，π₁，…）∈Π_m，如果对每个t∈N，都有π_t≡π₀，则称它为随机平稳策略，记作。全体随机平稳策略所组成的集合记作Π_s，并称为随机平稳策略类。

从上面的定义可以看到策略类之间的关系为：

且与F包含的元素一样多。在不引起混淆的地方，我们用F表示。