两载荷法实验原理

图4-1为两载荷测量原理示意图。图4-1（a）和图4-1（b）分别为2种不同的出口阻抗条件Za、Zb。对于图4-1（a）结构，传感器1和2之间、3和4之间为直管段，2和3之间为声学元件，其相应的传递矩阵为［24-25］

式中 pi，ui——各传感器处的声压和质点振速；

Ai，Bi，Ci，Di——各声学元件的四极参数；

i——各量的下标；

a，b——图4-1（a）和图4-1（b）中两种出口尾端情况。

图4-1 两载荷法测量示意图

对式（4-1）、式（4-2）和式（4-3）化简可得传感器2和3之间的四极参数关系式：

同理，对于图4-1（b）结构，可得传感器2和3之间的四极参数关系式：

令声压传递函数Hij=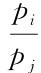，pi和pj分别代表传感器i和j处的声压，则由式（4-4）和式（4-5）可得：

式中：

设传感器1和2、3和4直管段中介质流动为平均流，忽略介质黏性，则直管段的四极参数：

式中 l12，l34——传感器1和2、3和4之间的距离；

M12，M34——1和2、3和4直管段内介质流动速度的平均马赫数；

k12——传感器1和2间直管段内流动介质的波数k12=k0/（1—M122）；

k34——传感器3和4间直管段内流动介质中波数k34=k0/（1—M342）；

k0——静态介质中波数k0=ω/c0；

ω——角频率；

c0——静态介质中声速。

M12=M34=0时，式（4-16）和（4-17）为无流条件下直管段的四极参数。

将式（4-16）和式（4-17）及测得的实验数据Hij代入式（4-6）—式（4-9）中，即可求得传感器2和3之间声学单元的四极参数，从而计算其传递损失为

式中 ρ0——介质的密度；

Si，So——消声器进、出口横截面面积。