高程测量用水平面代替水准面

图2－11 用水平面代替水准面对距离和高程的影响

当测区范围较小时，可以把水准面看作水平面。探讨用水平面代替水准面对距离、角度和高差的影响，以便给出限制水平面代替水准面的限度。

1．对距离的影响

如图2－11所示，地面上A，B两点在大地水准面上的投影点是a和b，用过a点的水平面代替大地水准面，则B点在水平面上的投影为b′。

设ab的弧长为D，ab′的长度为D′，球面半径为R， D所对圆心角为θ，则以水平长度D′代替弧长D所产生的误差ΔD为：

ΔD＝D′－D＝Rtanθ－Rθ＝R（tanθ－θ） （2－7）

将tanθ用级数展开为：

因为θ角很小，所以只取前两项代入式（2－7）得：

又因θ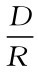＝，则

取地球半径R＝6 371km，并以不同的距离D值代入式（2－10）和式（2－11），则可求出，如表2－1所示。

表2－1 水平面代替水准面的距离误差和相对误差

结论：在半径为10km的范围内，进行距离测量时，可以用水平面代替水准面，而不必考虑地球曲率对距离的影响。

2．对水平角的影响

从球面三角学可知，同一空间多边形在球面上投影的各内角和，比在平面上投影的各内角和大一个球面角超值ε。

式中：ε——球面角超值（″）；

P——球面多边形的面积（km2）；

R——地球半径（km）；

ρ——一弧度的秒值，ρ＝206 265″。

以不同的面积P代入式（2－11），可求出球面角超值，如表2－2所示。

表2－2 水平面代替水准面的水平角误差

结论：当面积P为100km2时，进行水平角测量时，可以用水平面代替水准面，而不必考虑地球曲率对距离的影响。

3．对高程的影响

如图2－10所示，地面点B的绝对高程为HB，用水平面代替水准面后，B点的高程为HB′，HB与HB′的差值，即为水平面代替水准面产生的高程误差，用Δh表示，则

（R＋Δh）2＝R2＋D′2

上式中，可以用D代替D′，相对于2R很小，可略去不计，则

以不同的距离D值代入式（2－12），可求出相应的高程误差Δh，如表2－3所示。

表2－3 水平面代替水准面的高程误差

结论：用水平面代替水准面，对高程的影响是很大的，因此，在进行高程测量时，即使距离很短，也应顾及地球曲率对高程的影响。