控制器设计及证明

针对子系统动力学模型式(6.5)，设eqi＝qi-qdi，eτi＝τci-τdi，τdi为执行器末端分配到各关节的期望力矩，qdi为各关节期望位置，qi为各关节实际位置。当qi趋向于qdi时，eqi和eτi之间存在数值关系，所以定义滑模变量为

对式 (6.7) 求导， 得

取控制律

其中ki，kvi，kpi为正常数。在各关节子系统中，根据模糊系统的万能逼近理论[166]，采用模糊系统来逼近未知项 [167]，则:

其中θ＾ih为可调参数向量，为模糊基函数向量。

参数自适应律算法取为:

其中ηi为正常数，向量xi，矩阵P、B将在后续设计中给出。

设计非脆弱鲁棒控制项为

其中K为控制器增益， ΔK为增益摄动量。

将控制律式 (6.9a) 带入式 (6.8) 中， 且

其中εi为模糊系统的逼近误差，所以。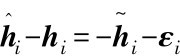

则

设，则其状态空间形式为

即

其中。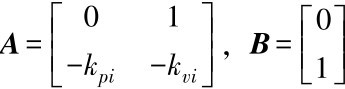

定理6.1: 对于式 (6.5) 的受限可重构模块机器人子系统， 基于给定的γi＞0，正定矩阵P，如果存在以下的LMI成立:

则控制律设计如式 (6.9a)， 参数自适应律如式 (6.9b)， 非脆弱鲁棒控制项如式 (6.9c)， 可使得:

(1) 可重构模块机器人系统渐近稳定且能跟踪期望的位置和力；

(2) 扰动信号到输出信号的传递函数满足如下跟踪性能:

证明: 取Lyapunov函数为

因为

其中，定义为扰动项。

将式 (6.15) 带入式 (6.16) 中， 得

将参数自适应律式(6.9b) 带入上式，其中γi＞0为指定的干扰抑制指标， 则

取

其中Q为正定对称矩阵， 则

对上式两边积分

因为Vi[x(T)]≥0，所以

满足跟踪性能。

由于，则存在δdi＞0使得成立，则式(6.20) 变为

λmin(Q)为矩阵Q的最小特征值。

对任意的σi＞0，使得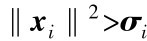，通过选择参数

此时， 根据Lyapunov稳定性理论， 可重构模块机器人系统渐近稳定且能跟踪期望的位置和力。

根据Schur补引理[168]，不等式(6.19) 等价于

得出定理成立的LMI条件， 定理得证。