其中M(q)、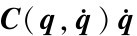
、G(q)、τ分别代表广义质量矩阵、哥氏力和离心力项、 重力项与外力项、 关节力矩向量。
可重构模块机器人的子系统动力学模型如下:
其中
设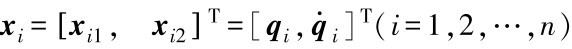
，式(7.2)可以用下面的状态方程表示:
其中
当发生执行器和传感器故障时， 机器人子系统的状态空间方程则变成:
其中fia和fis分别表示执行器和传感器故障函数，它们未知但有界。
假设7.1:当子系统执行器没有故障时fia＝0；有故障发生时，fia是上界已知的非零函数，即
，αia、ρi为正常数。
假设7.2:当子系统传感器没有故障时fis＝0；有故障发生时，fis是上界已知的非零函数，即
，αis、γi为正常数。
引入一个新的状态变量zi作为一阶滤波器的输出信号，其表达式为:
上式中yi表示关节位置的传感器输出信号，a、b都为非零常数且a大于零。
将式 (7.4) 代入式 (7.5) 中得
令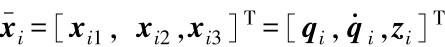
，则新的子系统状态变量方程为:
上式中
经证明已知
可控，
可观。
假设7.3:因为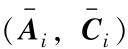
是可观的，则存在矩阵Li使得矩阵A0i＝
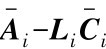并且存在Lyapunov方程如下:
上式中Pi、Ii为对称正定矩阵。
假设7.4:Pi、Fi的选择满足下式:
其中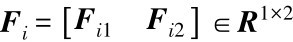
。
定义
，其中
分别为
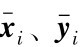的估计值。
针对式 (7.7) 所描述的子系统状态空间方程， 设计基于神经网络的非线性观测器:
其中βisgn
为鲁棒项， 用于抵消神经网络逼近误差对观测器的影响。
由式 (7.7) 和式 (7.10) 可以得到观测器所对应的误差动力学方程如下:
其中vi项用来补偿关联项对观测器的影响，用下式描述:
应用RBF神经网络对各子系统间的耦合关联项进行补偿， 即
上式中
是θip和σip的估计值，估计误差分别是
。
设神经网络理想的权值是θiw和θi Q，σ(˙)是神经网络的基函数，εi W和εi Q是逼近误差且是未知有界的。对系统的不确定项采用RBF神经网络进行逼近， 理想逼近状况如下:
定义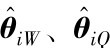
分别是θi W和θi Q的估计值，估计的误差分别为
，则
定义神经网络最小逼近误差如下:
上式中
为未知常数，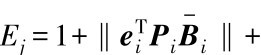
。
假设7.5:关联项
是有界的而且满足如下不等式:
假设7.6:神经网络最小逼近误差ωi是有界的，即
，其中βi为正常数。
参数的自适应律取为:
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
