各种位置直线的投影

3.2　各种位置直线的投影

空间一条直线的投影可由直线上的两点（一般取直线上的两个端点）来确定。例如，图3-7所示立体上的直线AB，求它的三面投影图时，可分别求出A、B两点的三面投影（a，a′，a″）和（b，b′，b″），然后将其同面投影相连接，即得直线AB的三面投影ab、a′b′和a″b″。根据直线在三投影面体系中的位置可以将其分为投影面垂直线、投影面平行线和投影面倾斜线。前两种直线称为特殊位置直线，后一种直线称为一般位置直线。

图3-7　直线的投影

3.2.1　投影面垂直线

垂直于一个投影面的直线叫投影面垂直线。它包括三种：垂直于H面的直线叫铅垂线；垂直于V面的直线叫正垂线；垂直于W面的直线叫侧垂线。它们的立体图、投影图和投影特性见表3-1。

表3-1　投影面垂直线

续表

3.2.2　投影面平行线

平行于某一投影面，同时倾斜于另外两个投影面的直线叫投影面平行线。平行于H面，倾斜于V面、W面的直线叫水平线；平行于V面，倾斜于H面、W面的直线叫正平线；平行于W面，倾斜于H面、V面的直线叫侧平线。表3-2列出了它们的立体图、投影图和投影特性。

表3-2　投影面平行线

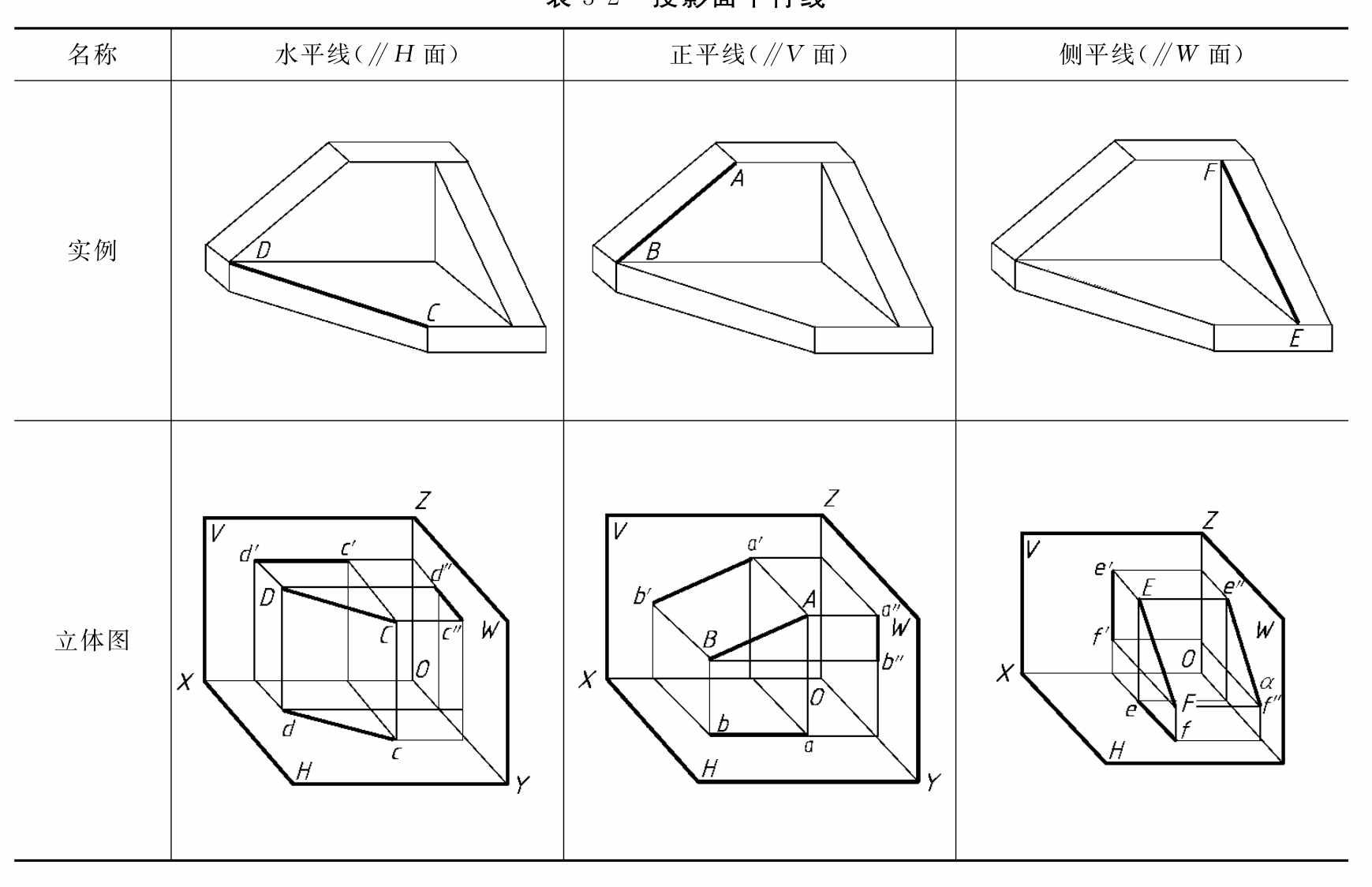
续表

3.2.3　投影面倾斜线

和三个投影面都倾斜的直线叫投影面倾斜线。它的投影特点是：三面投影都是斜线，三面投影的长度都小于空间直线的实长，见图3-2中的直线SA。

各种位置直线的投影特点是：

直线若是垂直线，一点对着二直线；

直线若是平行线，一斜对着二直线；

直线若是倾斜线，三面投影是斜线。

例3-4　如图3-8（a）所示，已知直线AB的两面投影ab、a′b′，求第三面投影，并说明叫什么直线。

图3-8　求直线AB的第三面投影

（a）题目；（b）作图方法

解　作图方法见图3-8（b）。

1）分别过点a′、b′作OZ轴的垂线；

2）在过点a′所作垂线上截取a″a_z＝aa_x，在过点b′所作垂线上截取b″b_z＝bb_x，连接a″、b″即为所求。

直线AB是铅垂线。

例3-5　如图3-9（a）所示，已知直线CD的两面投影cd、c′d′，求它的W面投影c″d″，并说明它叫什么直线。

图3-9　求直线CD的W面投影c″d″

（a）题目；（b）作图方法

作图方法见图3-9（b）。

1）分别过点c′、d′作OZ轴的垂线；

2）在两垂线上分别截取c″c_z＝cc_x，截取d″d_z＝dd_x，连接c″、d″即为所求。

直线CD是侧平线。

例3-6　如图3-10（a）所示，已知直线EF两面投影ef和e″f″，求它的V面投影e′f′，并说明它叫什么直线。

解　作图方法见图3-10（b）。

1）过点e作OX轴垂线，过点e″作OZ轴垂线，两垂线的交点e′即为点E在V面投影；

2）过点f作OX轴垂线，过点f″作OZ轴垂线，两垂线的交点f′即为点F在V面上的投影；

3）连接e′、f′即为所求。

直线EF是投影面倾斜线。

图3-10　求直线EF的V面投影

（a）题目；（b）作图方法