观测误差是系统误差还是偶然误差

5.1　测量误差的概念

5.1.1　观测值与观测误差

通过测量仪器、工具等任何手段获得的以数字形式表示的空间信息，称为观测值，例如用仪器观测地面上两点的角度值、距离值、高差值等。

对某一未知量在相同条件下进行若干次观测，每次所得结果是各不相同的。比如在测量中对一段距离、一个角度或两点间的高差在相同条件下进行多次重复观测都会出现这种情况。但是，只要不出现错误，每次所得的观测值是非常接近的，这些值与所观测的量的真值或理论值相差无几。我们把观测值与真值或理论值之间的差异称为观测误差，简称真误差或误差，用Δ表示。

若用L表示观测值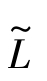，表示真值，则观测误差Δ的定义为

本单元讨论的对象与目的就是通过对误差的研究求得所观测量的最可靠值(最或是值)，评定观测的可靠程序(精度)。另一方面，为保证测量结果满足规范与施工精度的要求，保证质量，可以在未施测之前选用相应的一起类型和方法。

在测量过程中，也会因各种原因出现某些错误。错误时不属于误差范围的另一类问题。因为错误是由于粗心大意或操作错误所致，错误的结果与观测值的量无任何内在关系。尽管错误难以完全杜绝，但是可以通过观测与计算中的步步校核，把它从成果中剔除掉，保证成果的正确可靠。

5.1.2　误差的来源

观测误差产生的原因是多种多样的，但由于任何观测值的获取都要具备人、仪器、外界环境这三种要素，所以观测误差产生的原因可归结为下列三方面。

1.仪器工具的影响

仪器误差的影响可分为两个方面来理解:一是仪器本身固有的误差，给观测结果带来误差影响。如，用只有厘米分划的水准尺进行水准测量时，就很难保证在厘米以下的读数准确无误。二是仪器检校时的残余误差，如水准仪的视准轴不平行于水准轴而产生的i角误差等。

2.观测者的影响

人的感觉器官有一定的限度，特别是人的眼睛分辨能力的局限性，在仪器的安置、对中、整平、照准、读数等方面都会给测量成果带来误差。同时，在观测过程中操作的熟练程度、习惯都有可能给测量成果带来误差。

3.外界环境的影响

观测时所处的外界条件，如温度、湿度、风力、大气折光等因素都会对观测结果直接产生影响;同时，随着温度的高低、湿度的大小、风力的强弱以及大气折光的不同，它们对观测结果的影响也随之不同，因而在这种客观环境下进行观测，就必然使观测的结果产生误差。

上述仪器、观测者、外界环境三方面的因素是引起误差的主要来源。因此，我们把这三方面的因素综合起来称为观测条件。不难想像，观测条件的好坏与观测成果的质量有着密切的联系。当观测条件好时，观测中产生的误差平均说来就可能相对小些，因而观测质量也会高些。反之，观测条件差时，观测成果的质量就会低些。如果观测条件相同，观测成果的质量也就可以说是相同的。所以说观测成果的质量高低也就客观地反映了观测条件的优劣，也可以说，观测条件的好坏决定了观测成果质量的高低。

但是，不管观测条件如何，在整个观测过程中，由于受到上述因素的影响，观测的结果就会产生这样或那样的误差。从这个意义上来说，在测量中产生误差是不可避免的，即误差存在于整个观测过程中，称为误差公理。

5.1.3　误差的分类

根据观测误差对观测结果影响的性质，可将误差分为系统误差和偶然误差(随机误差)两种。

1.系统误差

在相同的条件下，做一系列观测，其误差常保持同一数值、同一符号，或者随观测条件的不同，其误差按照一定的规律变化，这种误差称为系统误差。例如，有一根长度(名义长度)为50m的钢尺，实际长度为49.9955m，用这根钢尺每量取一整尺就会比实际距离多出4.5mm，所丈量的距离越长，比实际长度多出的限值就越多;另外，用钢尺量距时气温的升降会使尺子相应地伸缩，所量的长度就会比实际长度偏大或偏小。再如，水准仪的水准管轴不平行于视准轴，进行水准测量时，水准尺距仪器的距离越大，其误差也会越大。所以，系统误差有积累的特性，符号与数值大小有一定的规律。系统误差的产生主要由仪器工具本身的误差和外界条件变化所引起。另一方面，观测者的习惯也能带来系统误差，这种误差通常是难以发现的。

对于系统误差可采用两种办法加以消除或抵消。第一种方法是通过计算改正加以消除，如在用钢尺量距时进行尺长、温度和倾斜的改正。第二种方法是在观测时采用适当措施加以抵消，如经纬仪观测时用正倒镜取平均值可以抵消视准轴不垂直于横轴和横轴不垂直于竖轴的误差，在水准测量中前后视距相等可以抵消水准管轴不完全平行于视准轴的误差，同时也可以抵消地球曲率和大气折光的影响。另一方面尽量提高观测者的技能与熟练程度，最大限度地减少人为影响。

2.偶然误差

在相同的观测条件下进行一系列的观测，如果误差在大小和符号上都表现出偶然性，即从单个误差看，该系列误差的大小和符号没有规律性，但就大量误差的总体而言，具有一定的统计规律，这种误差称为偶然误差。例如，观测时的照准误差，读数时的估读误差等，都属于偶然误差。

偶然误差产生的原因是多种多样的，且偶然误差与系统误差是同时发生的。如前所述，系统误差通过计算和在观测时采取相应措施加以消除或抵消，当然不可能完全为零，但却大大地减弱了。系统误差与偶然误差相对而言处在次要的地位，起主导作用的是偶然误差。所以，本单元讨论的对象就是偶然误差及其特性，以及在一系列带有偶然误差的观测值中，如何确定未知量的最或是值(最可靠值)及评定观测量的精度(质量)。

5.1.4　偶然误差的特性

从单个偶然误差来看，其出现的符号和大小没有一定的规律，但对大量偶然误差进行统计分析，就发现了规律，并且误差个数越多，规律越明显。

在相同的观测条件下观测了100个三角形的全部内角。由于观测结果中存在着偶然误差，三角形内角之和不等于三角形内角和的理论值(也称真值，即180°)。设三角形内角和的真值为X，三角形内角和的观测值为L_i，则三角形内角和的真误差Δ_i为

Δ_i=X－L_i　　　　　　(5.2)

现将217个真误差按绝对值大小及正、负号列于表5.1中。

表5.1　偶然误差统计表

从表5.1和图5.1中可以看出:小误差出现的个数比大误差出现的个数多;绝对值相等的正、负误差个数几乎相同;最大误差不超过18″。

图5.1　偶然误差统计直方图

通过大量实验统计，结果表明，当观测次数较多时，偶然误差具有如下统计特性。

(1)在一定的观测条件下，偶然误差的绝对值不会超过一定的限值，即有界性。

(2)绝对值小的误差比绝对值大的误差出现的可能性大，即偶然性或随机性。

(3)绝对值相等的正、负误差出现的可能性相等，即对称性。

(4)同一量的等精度观测，其偶然误差的算术平均值随着观测次数的无限增加而趋近于0，即

式中，［Δ］=Δ₁+Δ₂+…+Δ_n，n为观测次数。

在测量学中以“［·］”表示取括号中变量的代数和，即［Δ］=∑Δ。

偶然误差的第(4)个特性由第(3)个特性导出，说明偶然性误差具有抵偿性。

为了简单而形象地表示偶然误差的上述特性，今以偶然误差的大小为横坐标，以其相应出现的个数为纵坐标，画出偶然误差大小与其出现个数的关系曲线，如图5.2所示。这种曲线又称为误差分布曲线。误差分布曲线的峰越高坡越陡，表明绝对值小的误差出现较多，即误差分布比较密集，反映观测成果质量好;曲线的峰越低坡越缓，表明绝对值大的误差出现较少，即误差分布比较离散，反映观测成果质量较差。

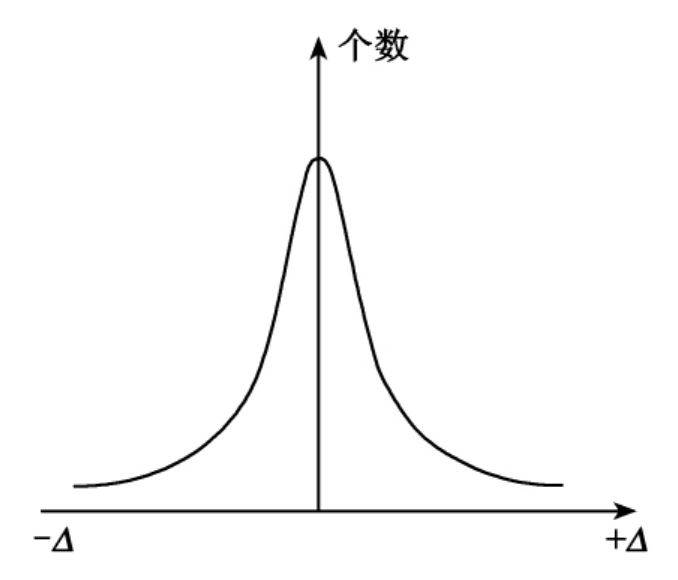
图5.2　偶然误差特性

偶然误差特性图中的曲线符合统计学中的正态分布曲线，标准误差的大小反映了观测精度的低高，即标准误差越大，精度越低;反之，标准误差越小，精度越高。