9.3 光纤传感器实例
9.3.1 光纤液位传感器

图9-22 光纤液位传感器
(a)Y型光纤;(b)U型光纤;(c)棱镜耦合
图9-22所示为基于全内反射原理研制的液位传感器。它由LED光源,光电二极管,多模光纤等组成。它的结构特点是,在光纤测头端有一个圆锥体反射器。当测头置于空气中,没有接触液面时,光线在圆锥体内发生全内反射而返回到光电二极管。当测头接触液面时,由于液体折射率与空气不同,全内反射被破坏,将有部分光线透入液体内,使返回到光电二极管的光强变弱;返回光强是液体折射率的线性函数。返回光强发生突变时,表明测头已接触到液位。
图(a)结构主要是由一个Y型光纤、全反射锥体、LED光源以及光电二极管等组成。
图(b)所示是一种U型结构。当测头浸入到液体内时,无包层的光纤光波导的数值孔径增加,液体起到了包层的作用,接收光强与液体的折射率和测头弯曲的形状有关。为了避免杂光干扰,光源采用交流调制。
图(c)结构中,两根多模光纤由棱镜耦合在一起,它的光调制深度最强,而且对光源和光电接收器的要求不高。
由于同一种溶液在不同浓度时的折射率也不同,所以经过标定,这种液位传感器也可作为浓度计。光纤液位计可用于易燃、易爆场合,但不能探测污浊液体以及会粘附在测头表面的粘稠物质。
9.3.2 光纤角速度传感器(光纤陀螺)
光纤角速度传感器又名光纤陀螺;其理论测量精度远高于机械和激光陀螺仪。它以塞格纳克效应为其物理基础。对于N匝光纤,塞格纳克相移为

式中符号见式(9-29)。
转速测量的误差是由光散粒噪声决定的。输出光电流可用式(9-26)计算。图9-23所示为光电流iD与相移φ,强度噪声iN与相移误差δφ的关系。光散粒噪声可按下列公式计算:

图9-23 光电探测器电流iD与相移φ的关系

对于零差检测方式,可用直线来近似曲线,得到
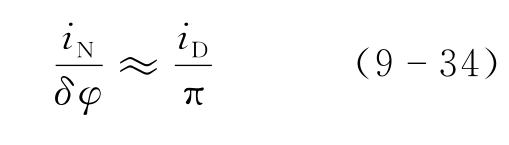
和

式中,B——噪声带宽:B≈1/2τ,其中τ为低通滤波器的时间常数。
将上式代入式(9-33)的微分式:δΩ=(λoc/4πNA)δφ可测得转速测量误差

式中nph——激光束中的光子数/秒。其他符号同式(9-13、9-3)。

图9-24 光纤陀螺
图9-24是光纤陀螺的最简单的结构。在光纤中,光传播的每一种模对实验环境波动的敏感性不同于其他模。因此,光纤角速度传感器的左旋光和右旋光虽然在同一光纤中传播,如果两个方向的传播模不一样,那么实验环境变化引入的相位差,将大于旋转产生的相位差。若能使整个光学系统限制在单模工作状态,当然可以解决这个问题,但这样做在技术上有一定难度。在图9-24的结构中,采用了偏振器和空间滤光器(在两透镜间的衍射小孔),只让一种模通过,使进入光纤两端的光工作于同一模。为了实现零差检测,需要对进入光纤某一端的光,相对于另一端相移π/2。为了避开低频端1/f噪声,也需要对信号进行调制,故在图中设置了调制器。光劈的作用是使光分成两束。
9.3.3 光纤电流传感器
图9-25为偏振态调制型光纤电流传感器原理图。根据法拉第旋光效应,由电流所形成的磁场会引起光纤中线偏振光的偏转;检测偏转角的大小,就可得到相应的电流值。如图

图9-25 偏振态调制型光纤电流传感器测试原理图
所示,从激光器发生的激光经起偏器变成偏振光,再经显微镜(×10)聚焦耦合到单模光纤中。为了消除光纤中的包层模,可把光纤浸在折射率高于包层的油中,再将单模光纤以半径R绕在高压载流导线上。设通过其中的电流为I,由此产生的磁场H满足安培环路定律。对于无限长直导线,则有
H=I/2πR (9-36)
由磁场H产生的法拉第旋光效应,引起光纤中线偏振光的偏转角为
θ=VlI/2πR (9-37)
式中,V——费尔德常数,对于石英:V=3.7×10-4(rad/A)
l——受磁场作用的光纤长度。
由此得 
受磁场作用的光束由光纤出端经显微物镜耦合到偏振棱镜,并分解成振动方向相互垂直的两束偏振光,分别进入光探测器,再经信号处理后输出信号
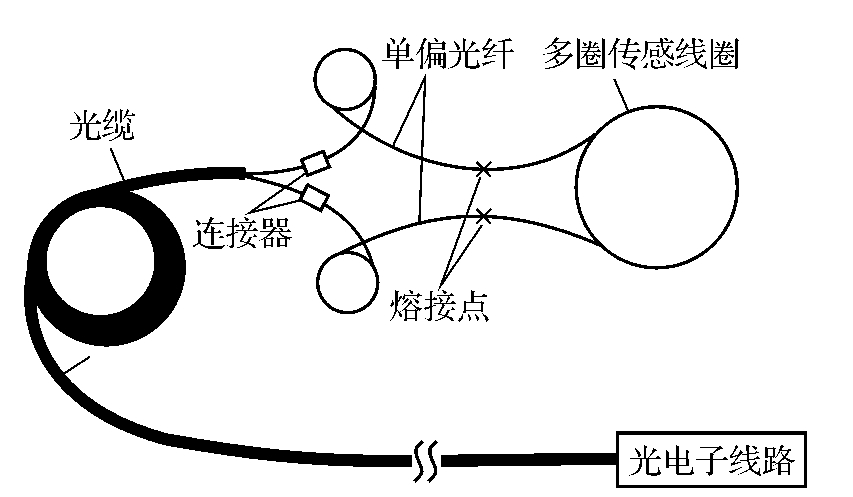
图9-26 全光纤结构电流传感器
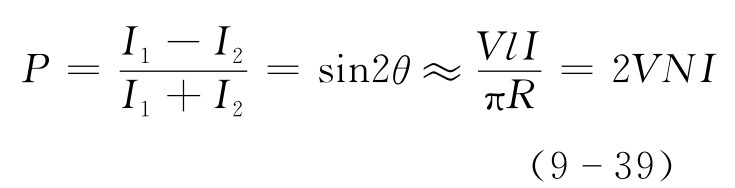
式中,N——输电线链绕的单模光纤匝数。
该传感器适用于高压输电线大电流的测量;测量范围0~1000A,精度可达1%。
图9-26为新近出现的一种全光纤结构的光纤电流传感器。其中单偏光纤代替了上述结构中的起偏器,并用了一个多圈传感线圈。电流测量范围可达0.1~5000A。
9.3.4 光纤光栅传感器[1]
光纤光栅传感技术是国际上近十年发展起来的新型传感技术。它是以光纤为载体的传感技术的最杰出代表,目前已成功应用于众多相关行业。所谓光纤光栅,就是一小段芯区折射率周期性调制的光纤。光纤光栅传感器(Fiberoptic Raster Sensor)就是通过检测每小段光栅反射回来的信号光波长值的变化,来实现对被测参数的测量。
1.光纤光栅的结构和工作原理
光纤光栅的结构如图9-27(a)所示。渐变型光纤的纤芯内掺杂有单晶锗离子。光栅的制作是通过写入技术,即通过紫外光干涉图案(周期图案)照射光纤,利用光纤材料的光敏性(入射光子与纤芯内锗离子相互作用)而造成折射率(10-5~10-3)的永久性变化,从而在纤芯内形成一小段一小段折射率周期性变化的空间相位光栅。这种光栅被称为光纤布拉格(Bragg)光栅(FBG)。

图9-27 布拉格光纤光栅的结构(a)和工作原理(b)
若光栅间隔周期Λ较短,当光束向光栅以一定的角度入射时,光波在介质中要穿过光栅的多个变化间隔,介质内各级衍射光会相互干涉,其中高级次的衍射光相互抵消,只出现0级和1级衍射光,即Bragg衍射。因此,入射进光纤的宽带光,只有满足一定条件的波长的光才能被反射回来,其余光即被透射出去,如图9-27(b)所示。
由耦合模理论可知,光纤光栅的Bragg中心波长为
λB=2neffΛ(9-40)
式中,neff为光纤有效折射率;Λ为光栅周期。
由上式可见,λB随neff和Λ变化而变化。而光纤受外界应变和温度影响将通过弹光效应和热光效应影响neff;通过光纤长度变化和热膨胀影响Λ,从而引起中心波长λB的改变。所以,光纤光栅传感器基本原理就是:利用光纤光栅有效折射率(neff)和周期(Λ)的空间变化对外界参量的敏感特性,将被测量变化转化为Bragg波长的移动,再通过检测该中心波长的移动来实现测量的。
2.解调技术
解调的目的就是要检测出反映被测量变化的FBG波长微小移动量。用于FBG波长编码解调的方法有滤波法、光谱编码/比例解调法、干涉法和可调光纤法布里-珀罗(Fabry-Perot,F-P)腔法(参见图9-18)。F-P腔法具有体积小、价廉、并能直接输出对应于波长变化的电信号的优点。
图9-28为可调F-P腔的解调方案。其中F-P腔可视为窄带滤波器。入射F-P腔的平行光只有满足相干条件的特定波长的光,才能发生干涉,形成相干峰值。光路过程为:宽带光源入射光经隔离器进入FBG光栅,由它反射回的光经耦合器和透镜,形成平行光入射到F-P腔;出射光再经透镜汇聚输入光电探测器,输出电信号。驱动元件采用了PZT压电陶瓷的逆压电效应,外加电压使其产生电致伸缩,使构成F-P腔的两个高反射镜中的一个移动,从而改变F-P腔腔长,使透过F-P腔的光波长发生改变。当F-P腔的透射波长与FBG反射波长重合时,入射探测器的光强最大(出现波峰)。
3.应用

图9-28 对FBG波长解调的可调F-P腔方案
图9-29为分布式FBG传感器网络。光纤通过写入技术形成FBG光栅传感器阵列1,2,…,n。把它布设于桥梁、大坝等大型土建工程或航空、航天器等特殊结构之中,就可在一条光纤上进行多点准分布式测量要害部位的应力、温度等参数,实现结构的“健康监测”。
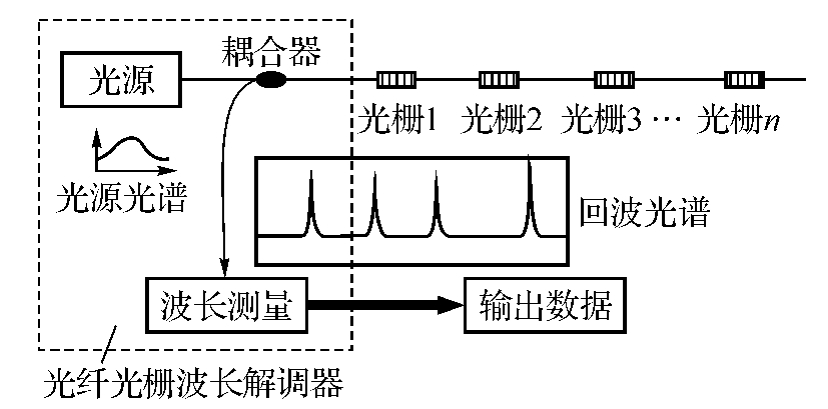
图9-29 分布式光纤光栅传感器网络
习题与思考题
9-1 试用射线分析方法,阐明阶跃光纤的导光原理,并解释光纤数值孔径的物理意义。
9-2 有一阶跃光纤,已知n1=1.46,n2=1.45,外部介质为空气,n0=1。试求光纤的数值孔径值和最大入射角。
9-3 举例说明光纤传感器各种调制方式的原理和应用。
9-4 如图9-6所示:反射式光强调制器的输出信号(如电压)与光源的稳定性和被测物表面的反射率有关。试问:能否设计一种结构可消除这两种不利影响?
9-5 试比较图9-19四种类型干涉仪结构的检测特点和典型的应用范围。
9-6 说明光纤激光多普勒测速的原理和系统的组成。
9-7 如图9-24所示的光纤陀螺,为了实现零差检测,进入光纤某一端的光,必须相对于另一端相移π/2。试证明:
(1)如不进行相移,探测器上光强随相位Δφ的变化为
I=Io(1+cosΔφ)/2
(2)如进行相移,则为 I=Io(1-sinΔφ)/2并讨论相移方法的优点。
9-8 试计算光纤陀螺由于光散粒噪声引起的测量误差(°/小时)。已知NA=0.3,λ0=0.6×10-7m,nph=3×1015光子/秒(相当于1mW),η0=0.3,τ=1s。
9-9 试计算:基于法拉第旋光效应的石英光纤工频变流电流传感器(参见图9-25)的光纤匝数N。已知:光纤线圈半径R=0.3m,电流有效值1000A,由其产生磁场引起光纤偏振光的最大偏转角为30°。
9-10 简述利用光纤光栅对大型复杂构件进行“健康监测”的原理。
【注释】
[1]本节由贾伯年作了改编
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















