姿态测定误差对激光脚点坐标的影响

4.3.5　姿态测定误差对激光脚点坐标的影响

由式(4.16)知，姿态测定误差为:

e^ΔRN=(ΔR_N－I)·R_N·(R_L·r+t_LG)　　　　　(4.25)

将ΔR_N、R_N、R_L、r代入上式并展开得:

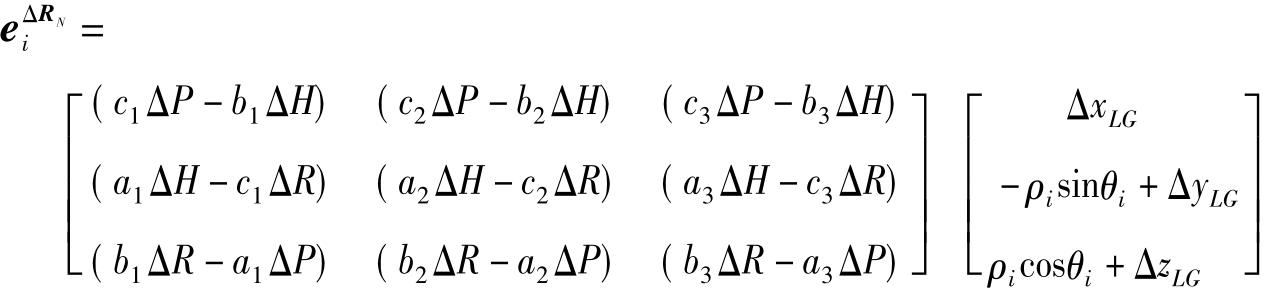
式中，

a₁=cosHcosP，　a₂=－sinHcosR+cosHsinPsinR　a₃=sinHsinR+cosHsinPcosR

b₁=sinHcosP，　b₂=cosHcosR+sinHsinPsinR，　b₃=sinHsinPcosR－cosHcosR

c₁=－sinP，　 c₂=cosPsinR，　　　　　　　　c₃=cosPcosR

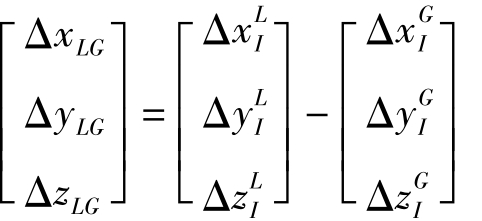
现讨论一种特殊状态的“正规化扫描线”(P=R=H=0)，即

a₁=1，a₂=0，a₃=0

b₁=0，b₂=1，b₃=0

c₁=0，c₂=0，c₃=1

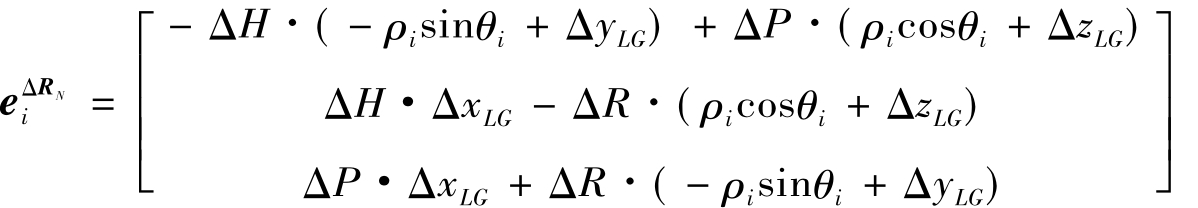
上式中，如果ΔP、ΔR、ΔH为百分之几度的水平，Δx_LG、Δy_LG、Δz_LG为米级，那么它们之间的乘积为毫米级，相对于其他误差而言是个小量，可以忽略。上式进一步简化为:

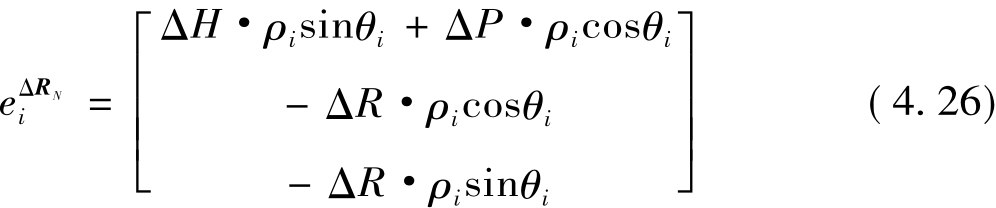
对于水平表面，测得的斜距可表示成飞行高度的函数H=ρ_icosθ_i，所以有:

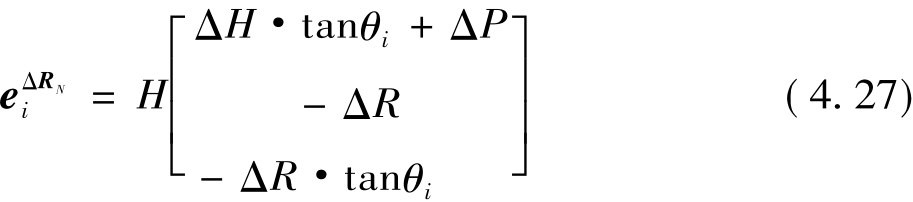
表4-2给出了相应的对于不同的姿态误差在不同的飞行高度及不同的扫描角条件下对激光脚点坐标产生的误差(刘经南等，2001)。

表4-2　　　　姿态误差对地面激光点坐标的影响

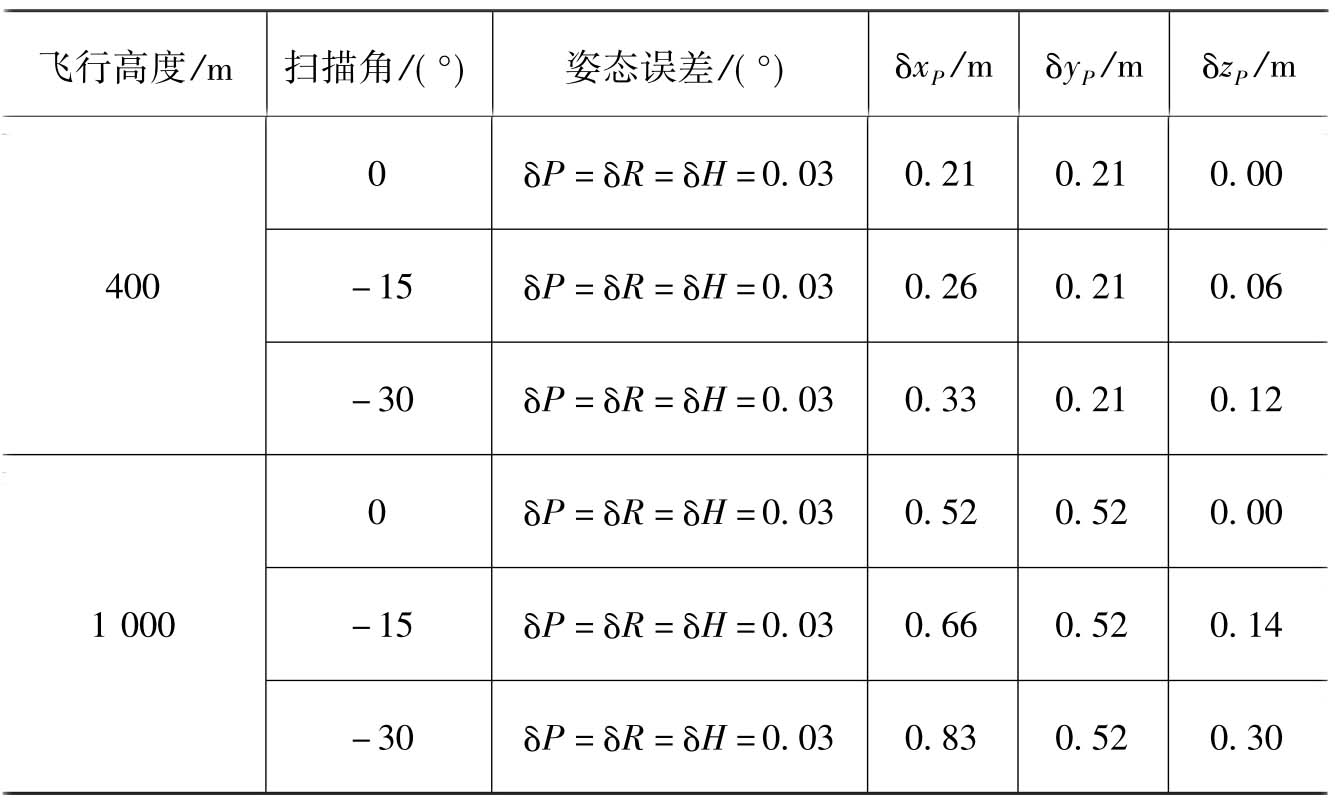
上面的计算结果表明，随着飞行高度的增加，姿态误差对地面激光点坐标的影响逐渐增大;随着扫描角的增大，姿态误差对地面激光点坐标的影响逐渐变大，高程方向的精度要比平面精度高。

如果飞机的姿态角较大时，如取P=10°，R=10°，H=30°，H=400m时，进行相同的模拟计算，结果见图4-5。

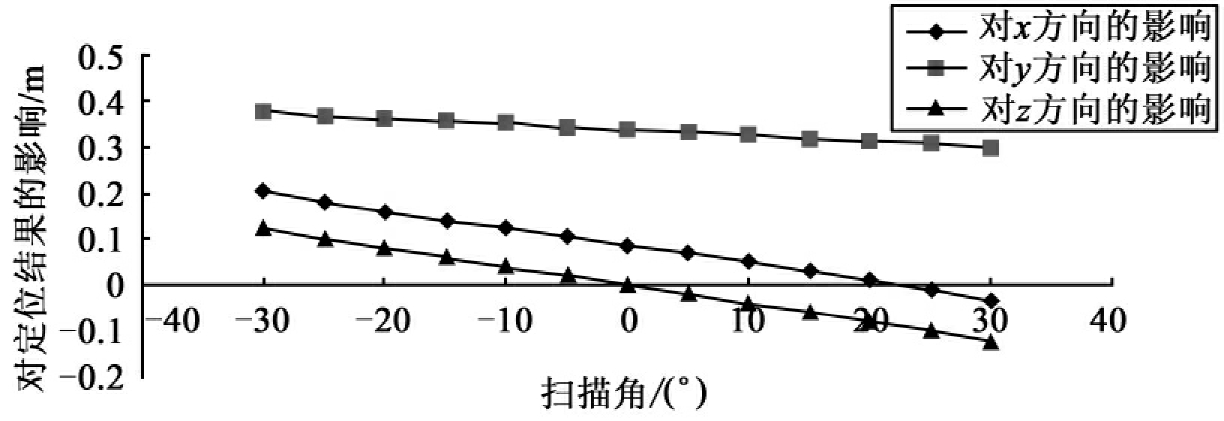
图4-5　姿态误差对地面激光点坐标分量x、y、z方向影响的变化曲线图

INS测定的三个姿态角的标称精度一般为百分之几度(Vaughn，et al，1996)。如果飞行高度小于300m，扫描角小于15°，按式(4.27)计算，由此带来的高程误差小于0.07m。在实际飞行作业过程中，姿态角误差一般不会超过0.05°，所以在低飞行条件下，姿态测量误差对机载激光雷达测量中激光脚点高程的影响并非主要因素。当然随着飞行高度的增加以及扫描角和姿态角的增大，其影响也不断增大，并成为主要的误差源之一。