【摘要】:点在一个投影面中的投影不能够反映点在空间的位置。为了统一,规定空间点用大写字母Α,B,C等标记,它们在H面上的投影用相应的小写字母a,b,c等标记,在V面上的投影用相应的小写字母加一撇如a′,b′,c′等标记,在W面上的投影则加二撇如a″,b″,c″等标记。然而空间点的任两个投影之间又都具有一个共同的坐标值。
二、点在三投影面体系中的投影
点在一个投影面中的投影不能够反映点在空间的位置。为了统一,规定空间点用大写字母Α,B,C等标记,它们在H面上的投影用相应的小写字母a,b,c等标记,在V面上的投影用相应的小写字母加一撇如a′,b′,c′等标记,在W面上的投影则加二撇如a″,b″,c″等标记。
由如图2-13所示得点的三面投影规律:
(1)正面投影和水平投影的连线垂直OX轴,即a′a⊥OX。
(2)正面投影和侧面投影连线垂直OZ轴,即a′a″⊥OZ。
(3)水平投影a和到OX轴的距离等于侧面投影a″到OZ轴的距离,即a a x =a″a z。
A a″=a ay=a′az=ax0=x A—A点到W面的距离;
A a′=a ax=a″az=ay0=y A—A点到V面的距离;
A a=a′ax=aa″ay=az0=z A—A点到H面的距离。
可见,空间点的任一面投影都是由该点的两个坐标值所决定的。即:
a是由A点的XA和YA两个坐标值决定的;
a′是由A点的XA和ZA两个坐标值决定的;
a″是由A点的YA和ZA两个坐标值决定的。
也就是说,空间点的任一面投影都反映了该点的两个坐标值。然而空间点的任两个投影之间又都具有一个共同的坐标值。即a与a′的X坐标值相同;a与a″的Y坐标值相同;a′与a″的Z坐标值相同。
根据点的投影规律,可由点的三个坐标值画出点的三面投影图,也可根据点的两面投影作出第三面投影。
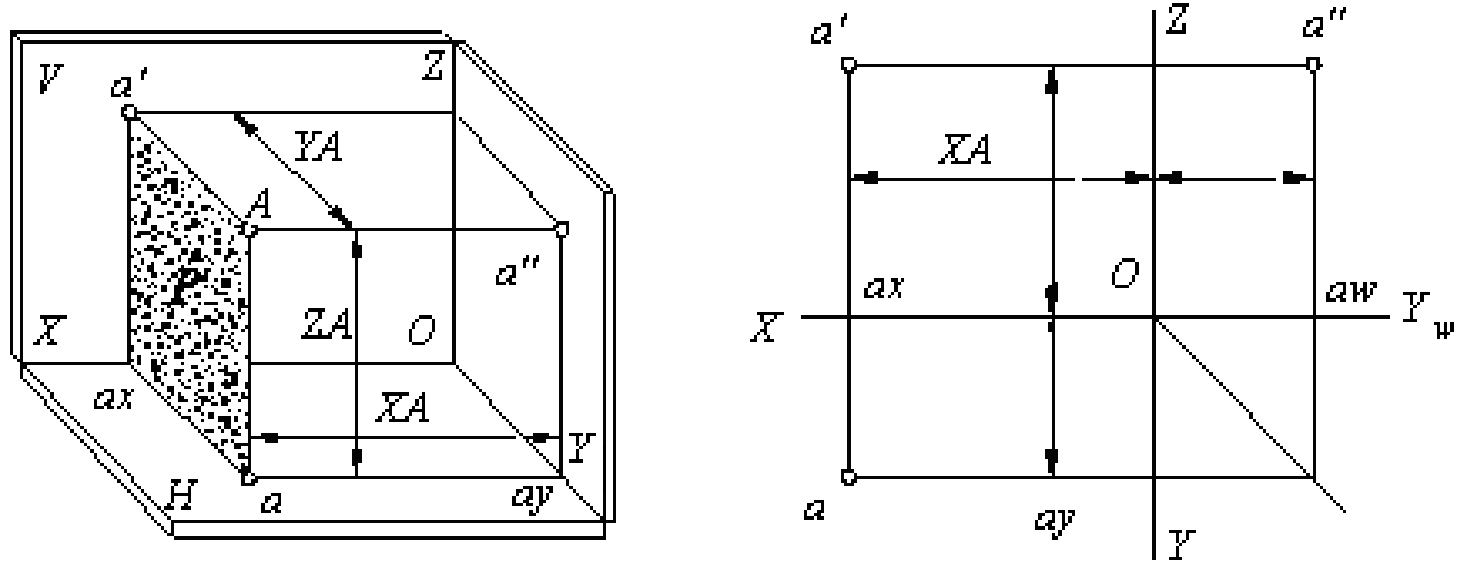
图2-13 点的三面投影规律
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















