节点计算举例

3.3.3　节点计算举例

已知条件如图3-11所示，下面用最容易理解的等间距法对图3-12中曲率变化不大的AS曲线段进行逼近计算。

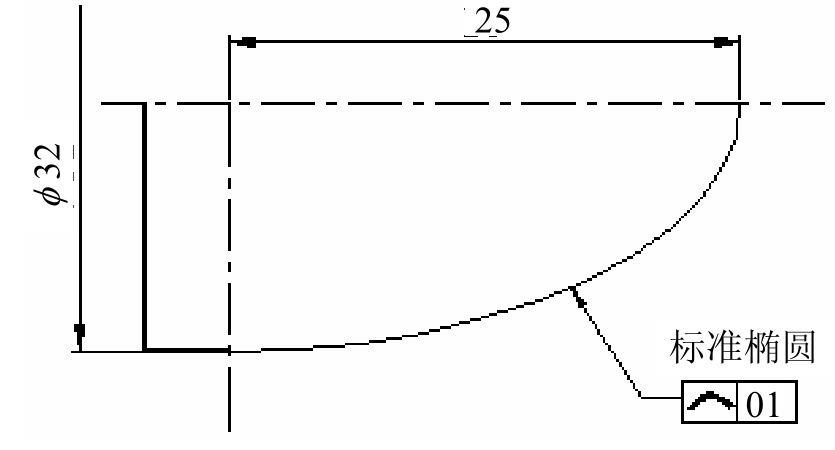
图3-11　逼近计算示例

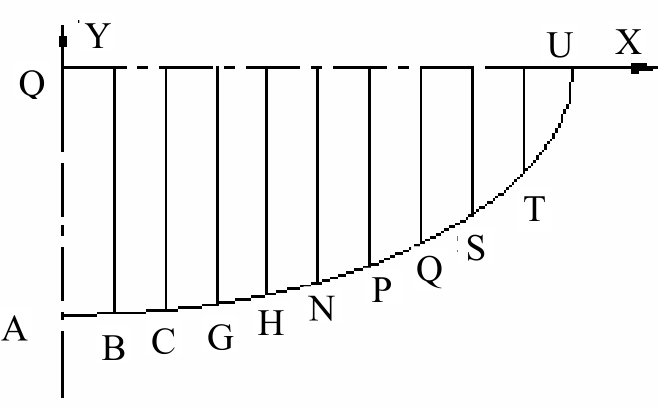
图3-12　逼近计算示例分析

1.分析

（1）根据已知条件和所设定的编程坐标系，可建立轮廓曲线方程为：

x²/a² + y²/b² = 1

式中：a——椭圆长轴；

　b——椭圆短轴。

（2）根据其曲线的走向位置，将轮廓曲线的总增量在横坐标轴上进行10等分后，得到B、C、G、H、N、P、Q、S和T等各节点。

（3）将各等分点的纵坐标值按曲线的椭圆方程式进行计算后，列于表3-3中。

表　3-3

（4）通过以上节点坐标值的计算表，可知：S、T、U处的曲率变化较大，不宜采用直线逼近法进行计算。故考虑只在节点A～S间用直线逼近法。

（5）在靠近Y轴处，曲线的曲率变化较小，可间隔5mm为一段进行插补。

（6）直线拟合过程采用边逼近边分析误差的方式进行。

1）如果分析得逼近误差很小时，可将分段长度适当增大，再进行逼近误差分析，以此类推。

2）如果逼近误差大于允许误差，则要相应缩小分段长度，再进行逼近误差分析，以此类推。

3）如果分段长度已经很小，而逼近误差仍然大于允许误差，则要考虑改用其他插补算法，如圆弧逼近算法。

2.计算步骤

（1）对A（x₁，y₁）、C（x₃，y₃）两点间的直线逼近

1）由直线方程的两点式：（y−y₁）/（y₁−y₃）=（x−x₁）/（x₁−x₃）

可得直线AC的一般形式方程：ax+by+c = 0

式中　　　　a=y1−y3，b=x3−x1，c=y1（x1－x3）−x1（y1−y3）

利用表3-3中的数据，可求出a、b、c，得直线方程为

0.32x−5y−80=0

2）利用点B（x₂，y₂）到直线AC的距离公式，可近似分析逼近误差。距离d的计算公式为：

d=│ax₂+by₂+c│/（a²+b²）^1/2

3）计算后的结果0.08mm已小于允许误差（图中所给定），故该逼近计算正确。

（2）对C、H两点间的直线逼近

1）建立直线CH的一般形式方程：1.02x−5y−83.5 =0

2）按上面的点线距离公式计算得d=1.09mm。

3）因误差大大超过了允许值，故必须减小逼近的分段间隔。

（3）减小分段间隔后，再对C、H两点间的直线逼近

1）在C、H两点间，按椭圆方程式计算出中点R的坐标值。

2）重复上述CH段的计算过程，直到误差小于允许值。

（4）按上述方法及步骤，依次完成其余各节点的直线逼近。

图中SU曲线段因为曲率变化较大，若还用直线逼近的方法，则会产生较大的逼近误差，所以宜采用圆弧逼近的方法。具体方法可以查阅有关资料，在此就不详述了。

通过以上分析和计算可知，节点的计算是相当复杂的，如果节点位置选择不当，会大大增加工作量。因此，在对轮廓曲线进行分段确定节点位置时，首先要分析该曲线在编程坐标系中的位置和走向，合理选定插补算法。例如：对轮廓上曲率变化不大的部分，可选择较大间隔的等分增量；对轮廓上曲率变化较大的部分，则应选择较小间隔的等分增量，或采用圆弧插补方法。这样不仅有助于选定较少的节点数，还有助于选用合适的逼近计算方法。