【摘要】:设关系R和关系S具有相同的目n,且相应的属性取自同一个域,则可定义并、差、交、广义笛卡儿积如下:设R为m元关系,S为n元关系,则R与S的广义笛卡儿积R×S是一个(m+n)元关系,其中的每个元组的前m个分量是R中的一个元组,后n个分量是S中的一个元组。若R有k1个元组,S有k2个元组,则R×S有个元组,即广义笛卡儿积:设两个关系R和S分别如图2-1和所示,则R∪S、RS、R∩S和R×S分别如图2-1、、和所示。
2.2.1 传统的集合运算
传统的集合运算是二元运算,包括4种运算:并(∪)、交(∩)、差(−)、广义笛卡儿积(×)。
设关系R和关系S具有相同的目n(即两个关系系都有n个属性),且相应的属性取自同一个域,则可定义并、差、交、广义笛卡儿积如下:
(1)并运算
关系R和S的并是一个新的关系,记为:
R∪S={t|t∈R∨t∈S}
R和S并的结果仍然是n元关系,它由属于R或属于S的所有元组构成。
(2)差运算
关系R和S的差是一个新的关系,记为:
R−S={t|t∈R∧t∉S}
R和S差的结果仍然是n元关系,它由属于R但不属于S的元组构成。
(3)交运算
关系R和S的交是一个新的关系,记为:
R∩S={t|t∈R∧t∈S}
R和S交的结果仍然是n元关系,它由属于R同时也属于S的元组构成。
(4)广义笛卡儿积
设R为m元关系,S为n元关系,则R与S的广义笛卡儿积R×S是一个(m+n)元关系,其中的每个元组的前m个分量是R中的一个元组,后n个分量是S中的一个元组。若R有k1个元组,S有k2个元组,则R×S有(k1×k2)个元组,即广义笛卡儿积:
R×S={t|t=〈tr,ts〉∧tr∈R∧ts∈S}
设两个关系R和S分别如图2-1(a)和(b)所示,则R∪S、R−S、R∩S和R×S分别如图2-1(c)、(d)、(e)和(f)所示。
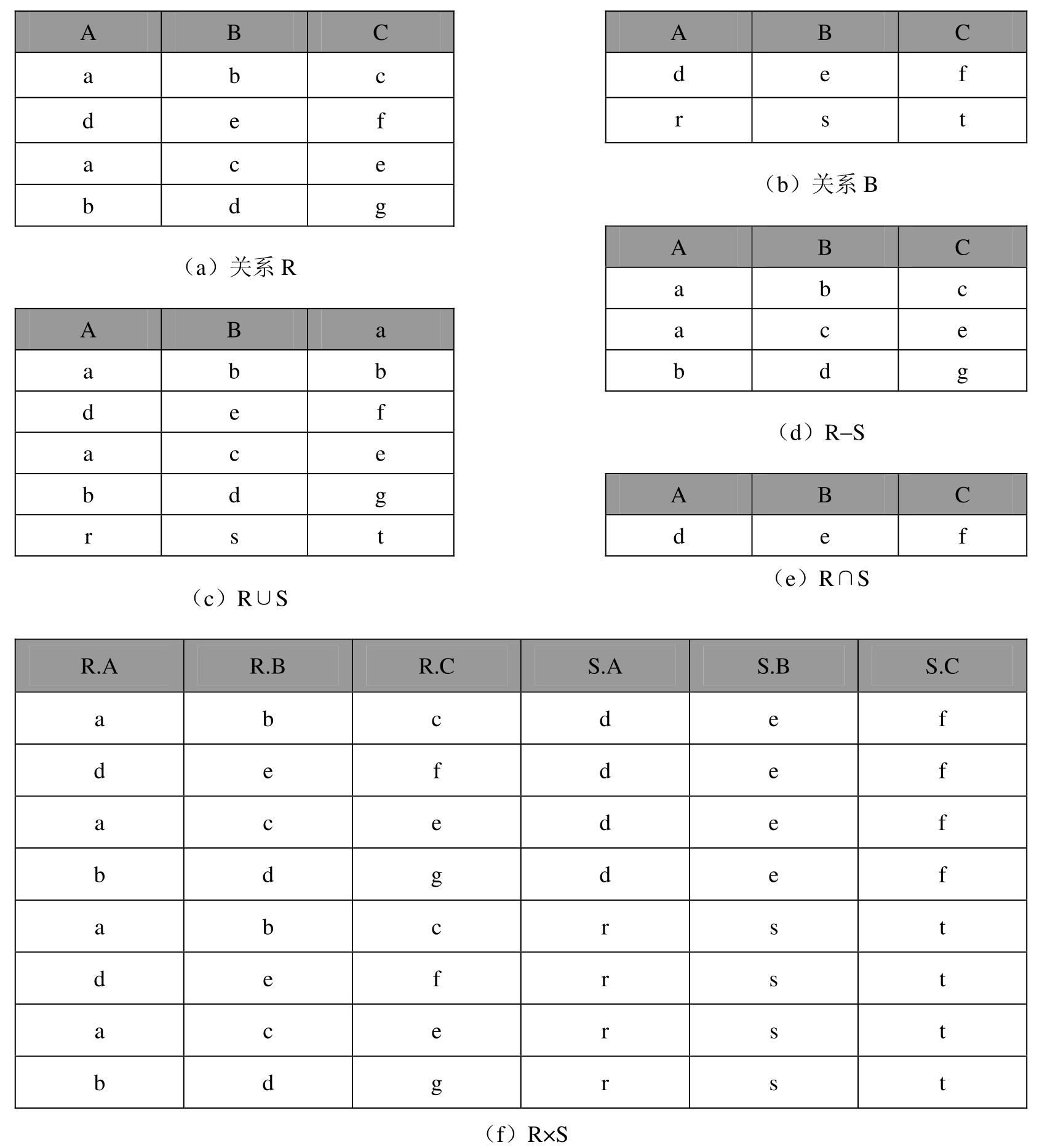
图2-1 关系代数传统集合运算的例子
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

















