10.3 检测数据处理分析
水工钢闸门动力测试所获得的一系列试验数据大多是以模拟量形式出现的时间历程记录曲线,通常称之为振动参量的波形,实测闸门振动记录曲线是一条较复杂的曲线,需要进行处理分析。检测数据的处理分析是通过数学的方法,突出闸门振动的有关信息,抑制和排除无关的信息,以便从复杂的现象中揭示其内在的规律性,把握事物的本质。
根据闸门振动的特点,振动信号可分为确定性信号和非确定信号。
1.确定性信号
确定性信号又称为规则信号。它是指振动量随时间变化而有确定的规律,能用明确的数学关系式描述,在相同试验条件下重复试验的信号基本不变。确定性信号按其特征又可分为周期性信号(谐波的)和非周期性信号(瞬态的)。一般结构的动力响应信号类似于周期信号。
2.非确定信号
非确定信号又称随机信号。它是指振动量随时间变化没有确定的规律,不能用确定的函数关系式来描述,在相同条件下重复试验,所测得的结构可能很不相同的信号。但在大量的重复测试中又呈现出一定的统计规律性,因而可以用概率统计的方法来描述和研究。闸门水流脉动激励及其动力响应都属于随机信号。
10.3.1确定性信号波形分析
确定性信号波形分析是指在幅值域和时间域内对确定性信号的波形进行各种分析。其目的是为了确定实测波形的最大幅值,各谐波分量的幅值、频率和相位滞后等。
10.3.1.1振动波形的幅值表示及计算
波形幅值有峰值、平均值和有效值等3种表示方式,如图10-6所示。
1.峰值
峰值表达式为
![]()
即振动参量(或测试信号)x的最大值。
2.平均值
其表达式为
![]()
对于简谐波形,x平均= 0.637x峰。
3.有效值
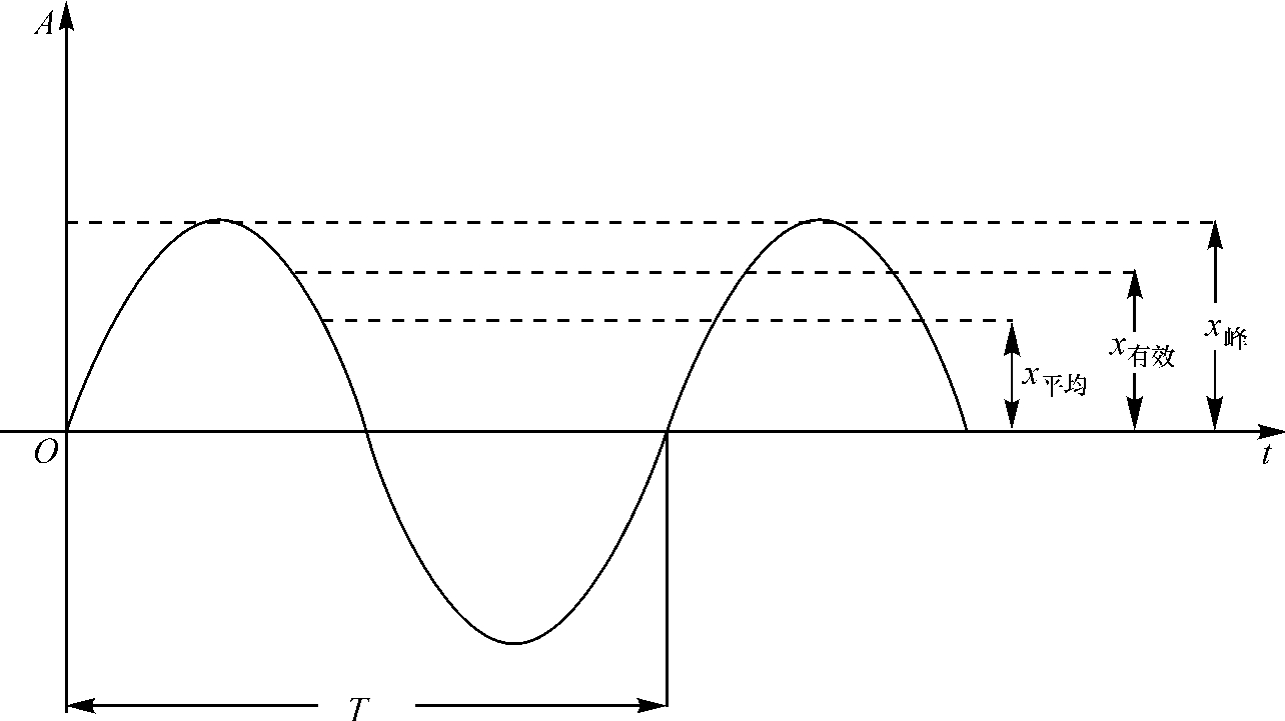
图10-6 正弦波的峰值、平均值和有效值
其表达式为
![]()
对于简谐波形,x有效= 0.707x峰
在闸门动力测试中,一般采用有效值来描述其幅值的大小。因为振动幅值与振动能量直接有关,该幅值也可能是速度或者加速度,其中位移的有效值代表振动体系(闸门)的势能,速度的有效值则代表振动体系的动能,加速度的有效值则代表振动体系的功率谱密度。此外,有效值还兼顾了振动过程的时间历程,而峰值只代表一个瞬时值,所以有效值在目前被认为是一个全面描述振动过程的指示值,因而被广泛采用。
在实际振动波形记录中,当基线不易确定时,读取波形峰-峰值即为被测全振幅值AP-P。可按式(10-34)计算实际振幅:
![]()
式中:K——仪器测试系统总的放大倍数;
β——仪器测试系统总的频响函数值。
10.3.1.2 振动波形的频率计算
对于确定性信号的振动波形,一般只要有测试振动信号的波长和时标信号的波长,就可算出被测试的波形频率。即
![]()
式中:l——振动信号的波长,mm;
l0——时标信号的波长,mm;
m——波长数目;
f0——时标已知频率,Hz;
v——记录纸移动的速度,mm/s。
10.3.1.3 振动波形的频谱分析
所谓频谱分析就是对振动信号在频率域内进行分析。此内容在下一节中专门介绍。
10.3.2 随机信号波形分析
水工钢闸门的水流脉动激励及其对闸门的动力响应等信号都属于随机信号,对其分析及处理仍然在幅值域、时间域和频率域内进行。
10.3.2.1 随机信号波形的幅值域分析
随机信号波形的幅值域分析的主要内容有均方值、均值和方差、概率密度函数等,具体分析如下。
1.均方值、均方根值
均方值表示随机信号的强度,它可定义为:
![]()
式中:x(t)——测试样本函数,即测试信号的时间记录曲线。
均方根值ψx是均方值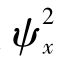 的正平方根值,即
的正平方根值,即
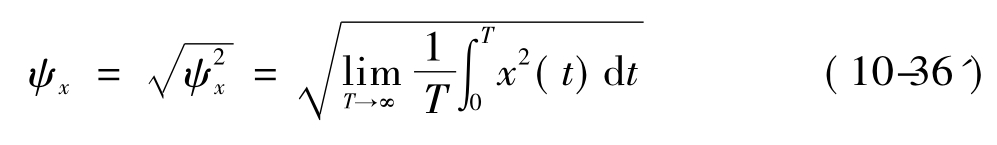
2.均值、方差和标准差
均值等于样本函数x(t)的时间平均值,即
![]()
T为样本长度或采样长度,单位为秒(s)。T→∞为理想情况,下同。
方差定义为:
![]()
标准差是方差的正平方根值,即
![]()
显然,方差是描述随机信号x(t)偏离其均值μx的程度,即均值μx是描述数据的静态分量,而方差、标准差是描述数据的动态分量。若将σ2的表达式展开得x

可见,均值、方差与标准差三者之间的关系为:
![]()
因此,随机信号的均方值包括静态分量和动态分量。由于均方值是提供数据强度方面的基本描述,则当随机信号表示振动速度或位移时,方差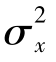 就是与随机振动的能量和功有关的量,它的单位是速度或位移的平方的单位,而振动体系的动能、势能及阻尼消耗的能量都是与之成比例的。当均值μx为零时,方差
就是与随机振动的能量和功有关的量,它的单位是速度或位移的平方的单位,而振动体系的动能、势能及阻尼消耗的能量都是与之成比例的。当均值μx为零时,方差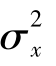 就等于均方值
就等于均方值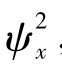 ,即
,即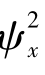 =
=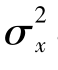 。
。
3.概率密度函数及概率分布函数
概率密度函数表示瞬时随机数据值落在某一指定范围内的概率。它的主要用途是用来描述随机信号瞬时值的概率及幅值分布情况。
概率密度函数定义为:
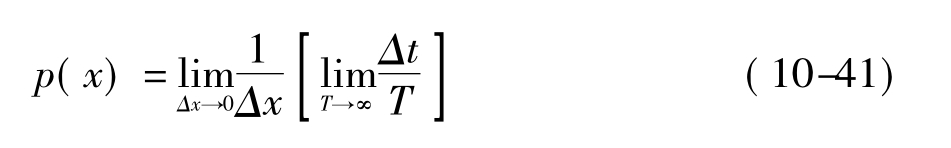
式中:T——样本记录时间(即采样时间);
Δt——表示在观察时间T内,样本记录x(t)落在(x,x+Δx)范
围内的总时间,如图10-7所示,则
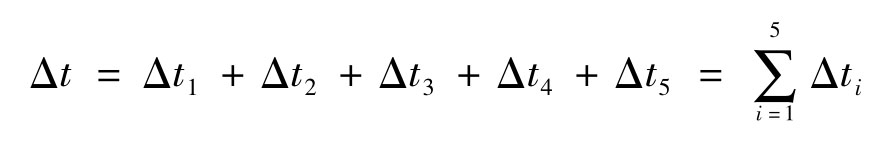
所以p(x)恒为实值非负函数。
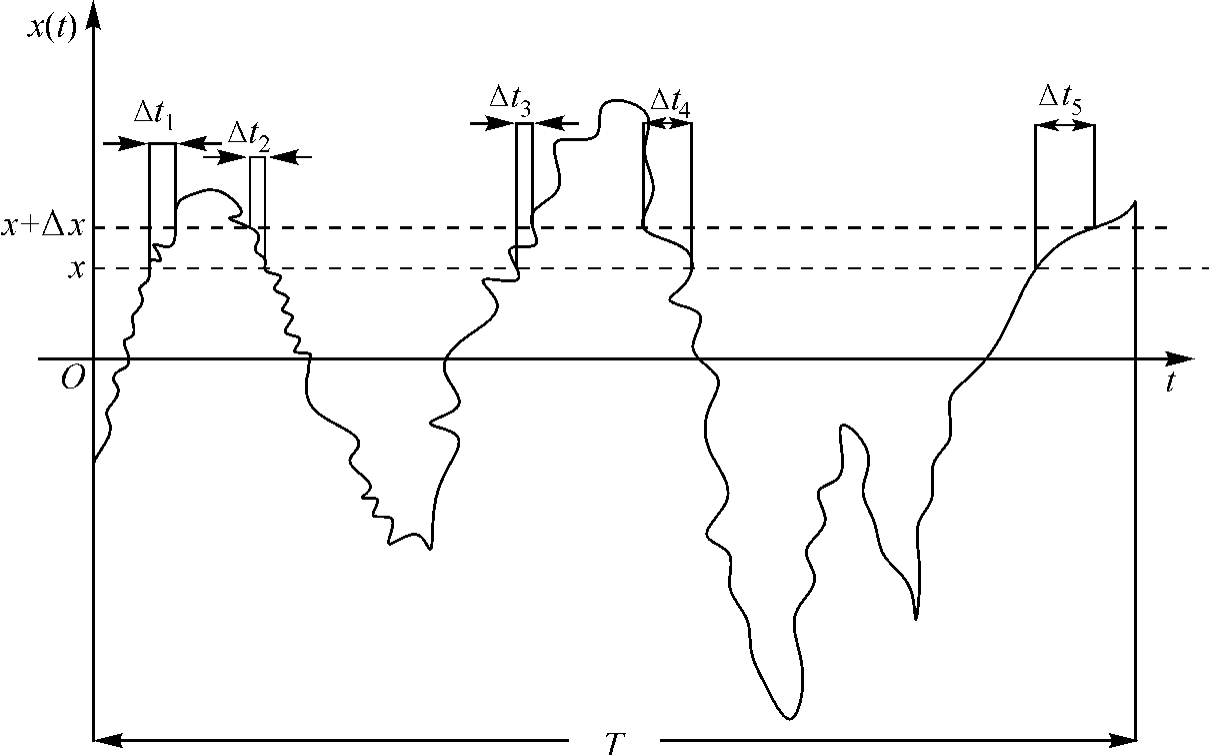
图10-7 概率测量图
概率分布函数可定义为:
![]()
如果一个随机过程x(t)是平稳的,t为任意值时的随机变量的概率密度函数和概率分布函数是相同的,都可以用x(t)计算出来。
由于用概率密度函数描述随机振动信号能全面地反映测试数据的波形,能够认识和区别各种不同的随机信号,因此,在随机振动研究中比较普遍和比较经常地使用概率密度函数,如图10-8所示。
10.3.2.2随机信号波形的时域分析
时域分析又称相关分析。相关分析的主要内容包括自相关函数和互相关函数。分析如下:
1.自相关函数
依概率论知识,2阶原点混合矩称为随机变量x(t)的自相关函数,用Rxx(τ)表示,定义为
![]()
式中:x(t)——样本函数在时间t的数据;
x(t+τ)——样本函数在时刻(t+τ)时的数据;
T——观测时间。
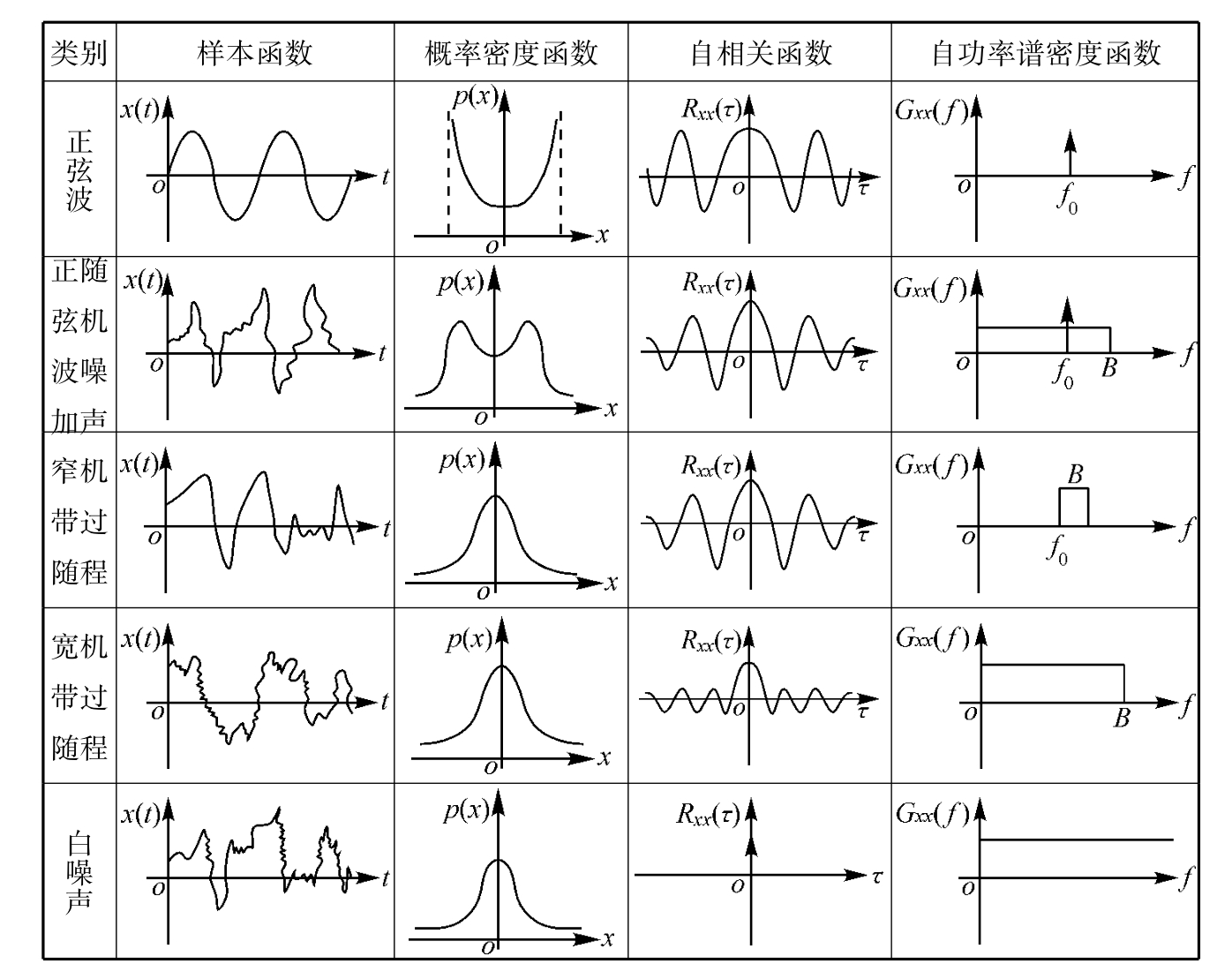
图10-8 5种典型振动信号的时间历程图及统计特征图
式(10-42)表示乘积x(t)·x(t+τ)在足够长的观测时间T内的平均值。它描述了随机过程某时刻t与另一时刻(t+τ)的数据值之间的依赖关系,即描述了随机过程不同时刻之数据值的相关关系。Rxx(τ)是以时间τ为自变量的实偶函数,可正可负,且在τ= 0时有最大值。在周期振动中,当τ= nT时,因为周期函数x(t)与x(t+τ)相同,它们有最大的相关性。而在随机振动中,x(t)与x(t+τ)不会相同,当τ→∞时,它们越来越不相关。此时,Rxx(τ)趋向一固定值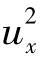 ,当ux= 0时,Rxx(τ)趋向零。在水工闸门测试技术中主要用来检验混杂在随机波形中的周期性信号。同时,它还能计算功率谱密度函数。几种典型的振动信号的自相关函数如图10-8中第3栏所示。
,当ux= 0时,Rxx(τ)趋向零。在水工闸门测试技术中主要用来检验混杂在随机波形中的周期性信号。同时,它还能计算功率谱密度函数。几种典型的振动信号的自相关函数如图10-8中第3栏所示。
2.互相关函数
若x(t)是一个随机信号的样本函数,而y(t)是另一个随机信号的样本函数,则这两组随机数据的互相关函数可定义为
![]()
式中:T是样本长度,τ是某一时间间隔,单位为秒(s),如图10-9所示。
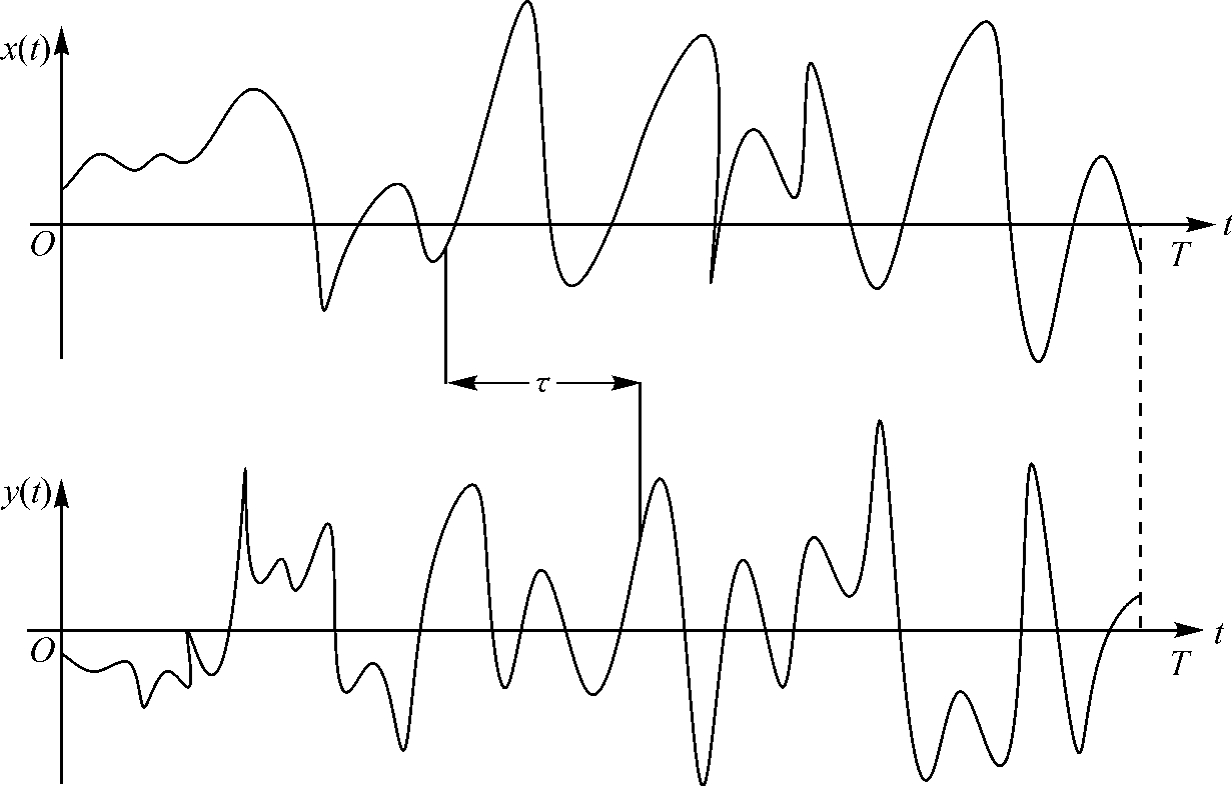
图10-9 互相关的两个样本函数
互相关函数Rxy(τ)是τ的函数,它描述两组数据值之间的依赖关系。某τ值时的Rxy(τ)也可以理解为图形x(t)与将y(t)向左平移τ所得图形y(t+τ)的相似性的描述。
Rxy(τ)是实值函数,可正可负。当Rxy(τ)= 0时表示x(t)与y(t)不相关。Rxy(τ)主要表示x(t)波形与y(t)波形移动τ时间差后,两者的相似程度。在水工钢闸门测试技术中,可用来确定信号的传递通道、计算功率谱密度函数和用于测试系统的脉冲响应函数。
10.3.2.3随机信号波形的频域分析
由于随机振动信号的随机性,它不能作幅值谱和相位谱分析,也不能用离散谱来描述,一般只能用功率谱分析。功率谱就是用连续来描述随机信号的幅值、相位和功率等随频率变化的连续分布情况。功率谱分析要求得到功率谱函数、凝聚函数和传递函数等。
1.功率谱(均方谱)密度函数
对水工钢闸门的随机振动信号进行频率分析时,一般要用到功率谱密度函数。功率谱密度函数可分为自功率谱密度及互功率谱密度函数,而自功率谱密度函数根据频率范围不同,又可分为单边谱和双边谱。功率谱密度函数一般由自相关函数推导出来。
自功率谱密度函数记为Sxx(f),根据傅立叶变换理论,假设自相关函数Rxx(τ)绝对可积,则可定义为:
![]()
式中:Sxx(f)——自功率谱函数,简称功率谱。
根据傅立叶积分理论,Sxx(f)的逆变换为Rxx(τ),故
![]()
自功率谱函数主要用来建立随机信号的频率结构,以便为分析其频率组成以及相应量的大小提供数据,几种典型随机信号的自功率谱图见图10-8第4栏。
自功率谱Sxx(f)中的f包括正值和负值,所以,Sxx(f)又叫做双边谱。现令即在Gxx(f)中,只有当f为正值时才存在。此时,Gxx(f)叫做单边谱,如图10-10所示。
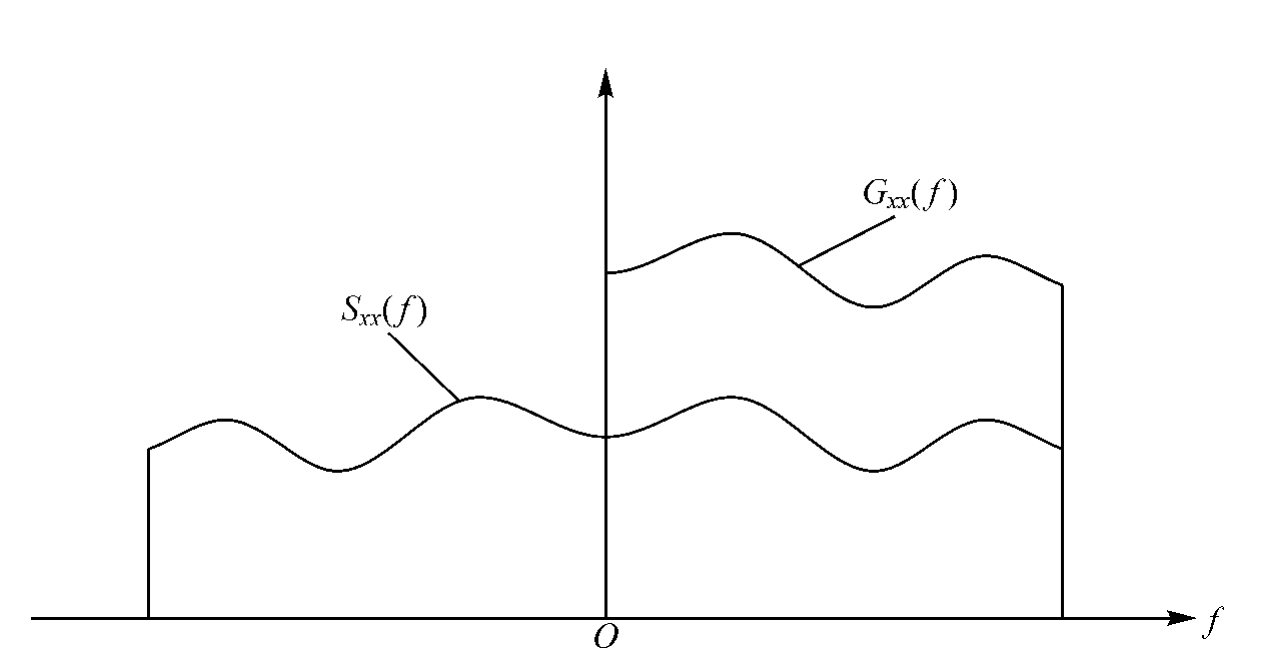
图10-10 单边谱与双边谱图
互谱密度函数记为Sxy(f),它是由两组随机数据的互相关函数的傅立叶变换直接求得的。即两个各态历经随机过程的样本函数x(t)、y(t)中,若Rxy(τ)是它们的互相关函数,当其绝对可积条件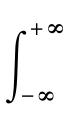 +∞-∞Rxy(τ) dτ<∞成立时,则可定义双边互谱密度为
+∞-∞Rxy(τ) dτ<∞成立时,则可定义双边互谱密度为
![]()
f的取值范围为(-∞,+∞)。
Sxy(f)的相应逆变换是
![]()
由于Rxy(τ)不是偶函数,所以双边互谱密度函数Sxy(f)是复数,可表示为:
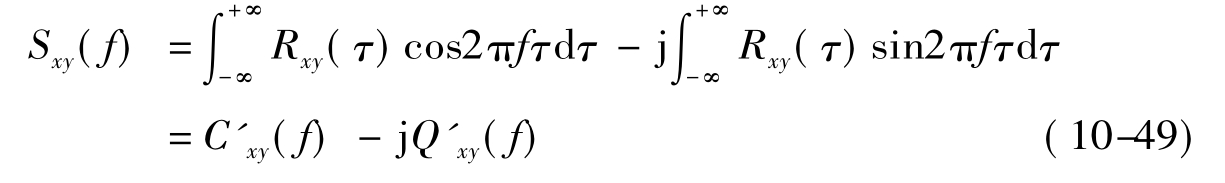
![]()
是f的偶函数;
![]()
是f的奇函数。
如上所述,若用单边互谱,其频率f只取正值,单位赫兹(Hz),单边互谱可定义为:
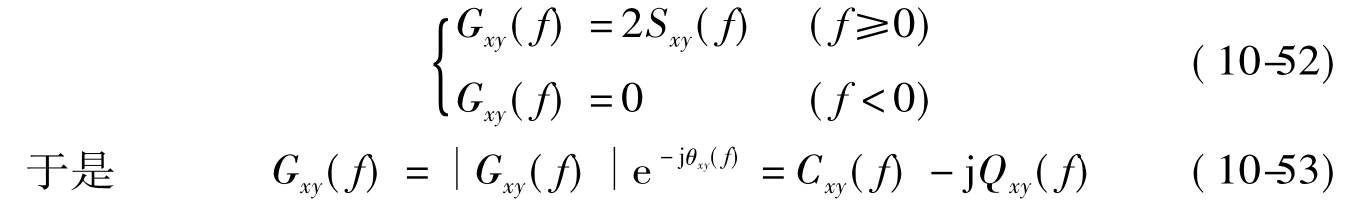
式中:实部Cxy(f)称为单边共谱、协谱或余谱;
虚部Qxy(f)称为单边正交谱、方谱或重谱;
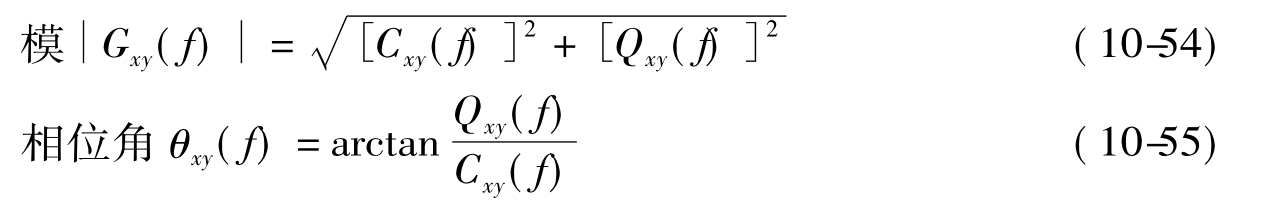
显然有
Cxy(f)= 2C'xy(f) (f≥0)
Cxy(f)= 0 (f<0)
Cxy(f)= 2Q'xy(f) (f≥0)
Cxy(f)= 0 (f<0)
互谱满足如下不等式:
![]()
2.传递函数(频率响应函数)及测量滞后时间
可依功率谱来研究体系的传递函数与测量滞后时间。若在闸门的某点单点输入一平稳随机信号x(t),则其任一点i的输出也是平稳随机信号,记为yi(t)。根据随机振动理论,对应于该输入点与输出点的体系的传递函数可由
![]()
求得。这是互谱密度函数在闸门动力试验中的重要应用,特别是闸门的模态分析及系统的动态特性参数识别中常用到。至于H(f)的测试精度的置信程度可通过计算相干函数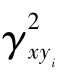 (f)得到。
(f)得到。
此外,若闸门输入为x(t),输出为yi(t),其互谱的相角θxyi(f)表示当频率为f时的简谐输入、输出信号间的相位差。因此,在任一频率f处信号通过闸门的滞后时间为:
![]()
3.凝聚函数(相干函数)
凝聚函数是在频率域内描述两种平稳随机过程x(t)与yi(t)的相关关系,又称相干函数。记为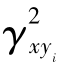 (f),定义为:
(f),定义为:
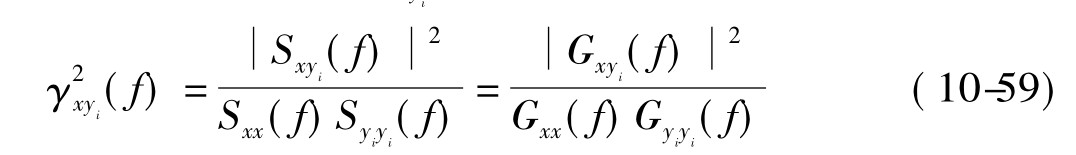
式中:Sxyi(f)、Gxyi(f)——分别表示随机过程x(t)与yi(t)的双边、单边的互谱密度函数;
Sxx(f)、Gxx(f)——分别表示随机过程x(t)的双边、单边的自谱密度函数;
Syiyi(f)、Gyiyi(f)——分别表示随机过程yi(t)的双边、单边的自谱密度函数。
显然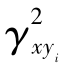 (f)是频率的函数,且为实数。
(f)是频率的函数,且为实数。
从式(10-59)可知:
(1)当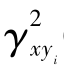 (f)= 1时,表示两种平稳随机过程x(t)与yi(t)之间完全相关,完全凝聚,即表示输出yi(t)完全是该输入x(t)引起的,干扰等于零。
(f)= 1时,表示两种平稳随机过程x(t)与yi(t)之间完全相关,完全凝聚,即表示输出yi(t)完全是该输入x(t)引起的,干扰等于零。
(2)当在某一频率fi上的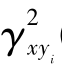 (fi)= 0时,表示两种随机过程x(t)与yi(t)在此频率fi上是不相干的。若在所有频率f上的
(fi)= 0时,表示两种随机过程x(t)与yi(t)在此频率fi上是不相干的。若在所有频率f上的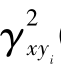 (f)= 0都成立,则表明两种随机过程x(t)与yi(t)是完全独立的、不相干的、不凝聚的。
(f)= 0都成立,则表明两种随机过程x(t)与yi(t)是完全独立的、不相干的、不凝聚的。
(3)在0≤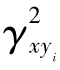 (f)≤1中
(f)≤1中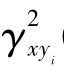 (f)越小表示输入x(t)与输出yi(t)之间的关系越小,即越不相干,越不凝聚。
(f)越小表示输入x(t)与输出yi(t)之间的关系越小,即越不相干,越不凝聚。
我们由式(10-56)亦可证明:
![]()
在工程实际中,一般当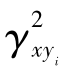 (f)≥0.707时,就认为两种随机过程x(t)与yi(t)是相干的、凝聚的。就可用它来判断、评定频率响应(传递函数)函数测试结果的好坏了。
(f)≥0.707时,就认为两种随机过程x(t)与yi(t)是相干的、凝聚的。就可用它来判断、评定频率响应(传递函数)函数测试结果的好坏了。
10.3.3试验数据的回归分析
回归分析是对测试数据分解处理的重要内容,因为通过回归分析可找到一个比较符合事物内在规律的数学表达式,以此来揭示和描述变量之间的相互关系。回归分析作为钢闸门检测技术中的一个重要问题,已在9.7节介绍过,本节不再叙述。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















