光纤的偏振和双折射特性

任务三　光纤的偏振和双折射特性

◆知识点

¤　光纤的偏振特性

¤　光纤的双折射效应

◆任务目标

¤　掌握光纤的偏振态变化

¤　理解光纤的双折射效应

¤　分析光纤传输光波产生拍的原因

任务导入：

传播的电磁波沿传输方向以一定的角度有它的电场和磁场。假如电磁波的传播方向是Z轴方向，那么电场方向可以为垂直于Z轴平面内的任何方向。电磁波的偏振（也称极化）描述当它通过介质传输时其电场特性。假如电磁场振荡所有时间都是线性，此时称该电磁波为线性偏振，场振荡和传播方向决定了一个偏振平面（振荡平面），因此线性偏振暗示该电波是平面偏振波。

任何非极化光线进入各向异性晶体后，将折射分成两束正交的线性偏振光，以不同的偏振态和相速度经历不同的折射率传输，这种现象称为双折射。

相关知识：

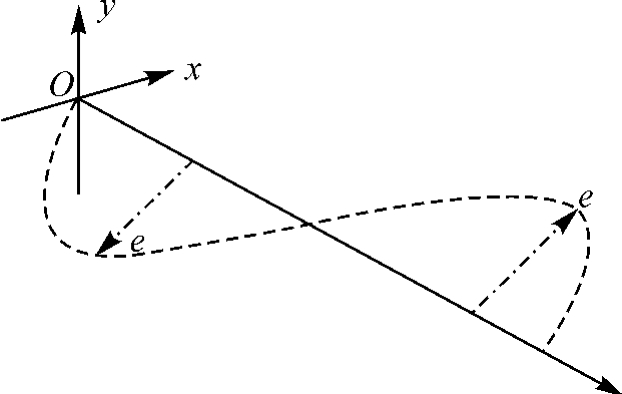
图2.11　偏振光波

1.平面波

光波是一个横波，其传播方向垂直于电场（E）和磁场（H）的振动方向。

给定一个空间直角坐标系O-xyz（如图2.11所示），假设一列平面波始终沿z方向传播，那么这列波可测量的电场可以表示为：

E（z，t）＝eEcos（ωt-kz）　　　　　　　　（2.6）

其中，e为电场振动方向，ω为光的角频率，k＝2π／λ为传播常数，表征相位变化的快慢。

2.光纤的偏振

通常单模光纤只传播HE₁₁一种模式。在理想情况下（假设光纤为圆截面，笔直无弯曲，材料纯净无杂质），此时HE11模为垂直于光纤轴线的线偏振光。根据光的电场矢量在xy平面上的运动轨迹，可以将光分为：线偏振光，椭圆偏振光，圆偏振光。

电场矢量在xy平面上的运动轨迹为一条直线的光称为线偏振光，它可以表示为两个相互正交的偏振光（如图2.12所示）。

E（z，t）＝Ex（z，t）＋E_y（z，t）　　　　　　　　（2.7）

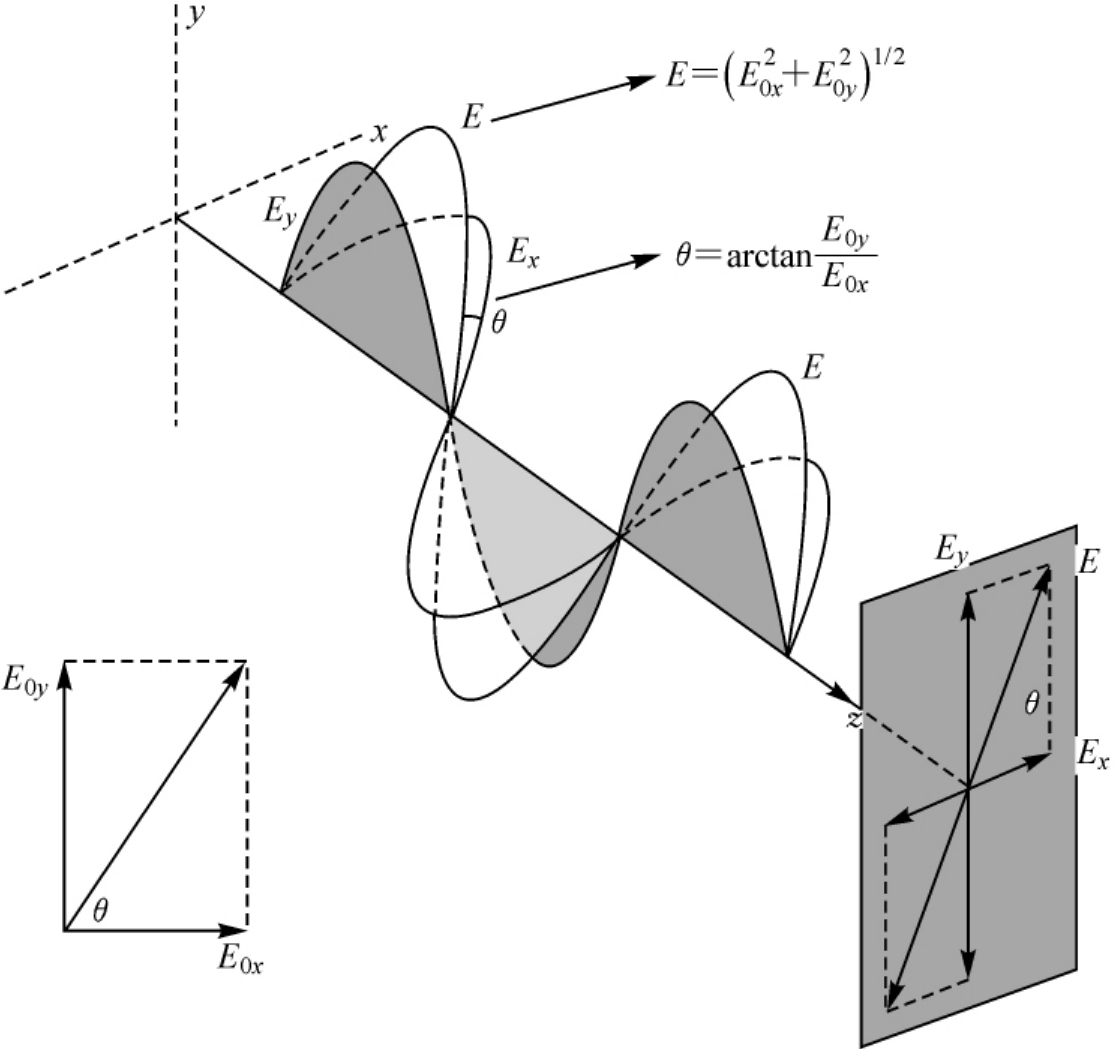
图2.12　光波的偏振性

E（z，t）＝e_xE_0xcos（ωt-kz）　　　　　　　　　　（2.8）

E（z，t）＝e_yE_0ycos（ωt-kz＋φ）　　　　　　　　（2.9）

这两个垂直分量之间的相位，差满足φ＝2mπ，其中m＝0，±1，±2，…；当d≠2mπ，m＝0，±1，±2，…时为椭圆偏振光；特别地，当两个相互正交的分量E0x＝E0y＝E0，且二者之间的相位差δ＝±π／2＋2mπ时，椭圆偏振光变成圆偏振光：迎着光传播的方向观察，根据δ取π／2和-π／2，圆偏振光分为右旋圆偏振光和左旋圆偏振光。

3.光纤的双折射

实际情况下上述理想条件是很难达到的。在单模光纤中传输的基模HE11是由两个偏振方向相互垂直的线偏振模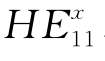和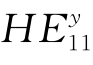所构成的（如图2.13所示），对于理想的均匀各向同性直圆柱光纤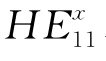，和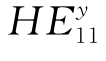的传播常数相同，即具有相同的相位，则合成光场是一个方向不随时间变化的线偏振场。实际由于光纤结构的不完善，光纤中总含有一些非对称因素，使两个本来简并的模式传播常数出现差异，而在光纤中以不同的相速度传播。如果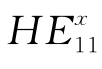和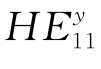存在相位差φ，线偏振态沿光纤不再保持不变，其偏振状态将沿着光纤长度以光频作周期变化（线偏振—椭圆偏振—椭圆偏振—线偏振），这种现象称为光纤的双折射效应。

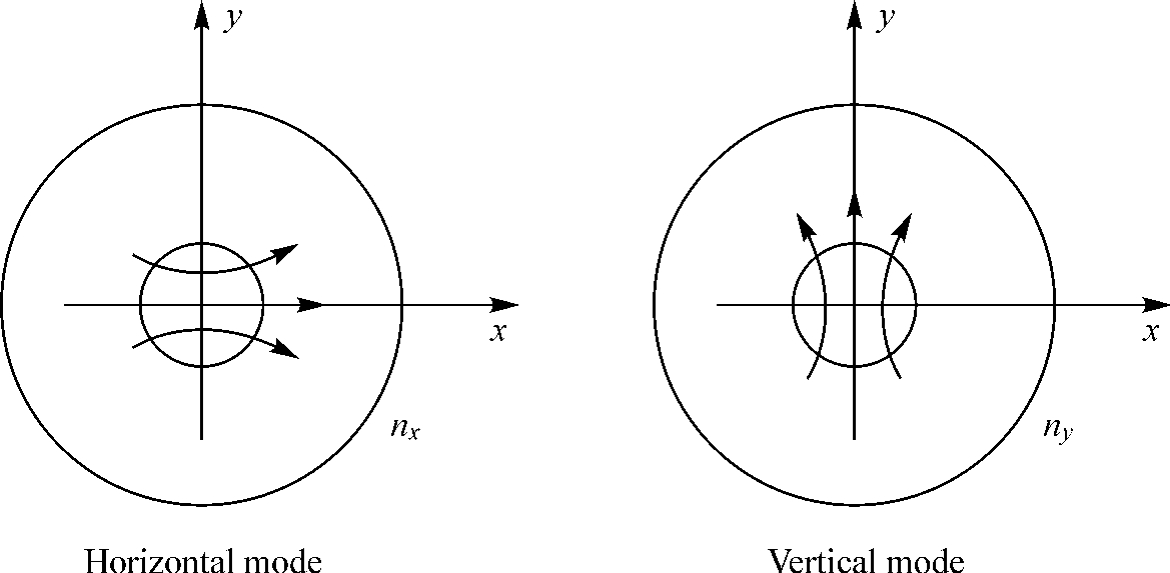
图2.13　HE₁₁偏振态相互正交的两个简并模

这种双折射效应可用归一化双折射系数B或拍长LB来描述。

光纤的双折射大小由双折射参数B表示为：）

式中Δβ为两正交线偏振模传播常数之差，K0为单模光纤平均传播常数。

两个简并模在传播时会产生相位差。当二者相位差为2π整数倍时，则光的偏振态与入射点相同，此时称该点处出现“拍”，如图2.14所示。两个拍之间的间隔称为“拍长”。

通常拍长在10cm～2m之间。

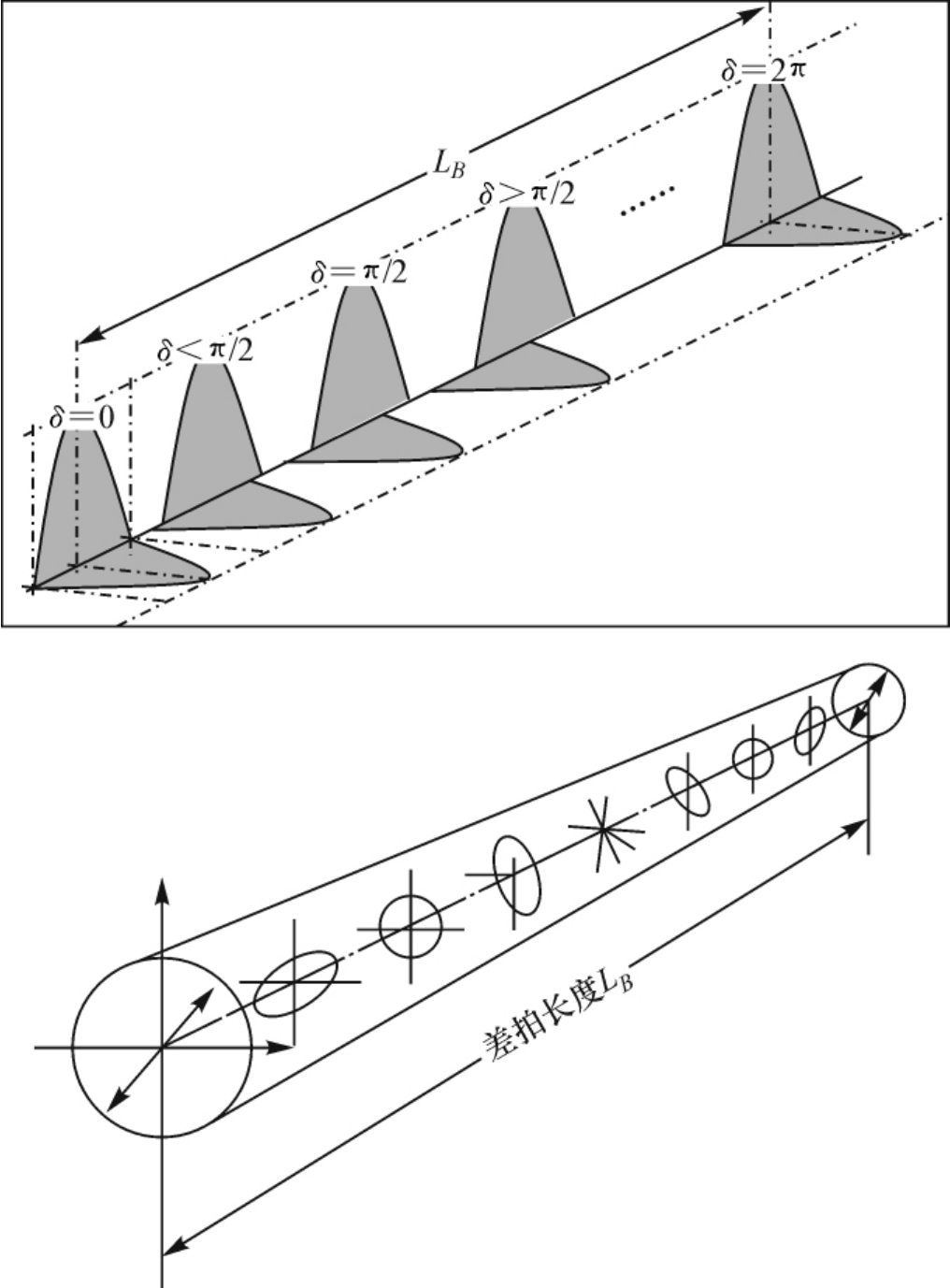
图2.14　单模光纤光偏振态呈周期变化“拍”

相关参数测量：

在单轴晶体中，两个正交的偏振光称寻常光（E⊥）和非寻常光（E∥）。寻常光在所有的方向具有相同的相速度，电场垂直于相速度的传输方向；非寻常光的相速度与传输方向和它的偏振态有关，而且电场不垂直于相速度的传输方向。

假如L是晶体片的厚度，寻常光（o）通过晶体经历的相位变化是K₀L，K₀＝（2π／λ）n₀是寻常光波矢量，而非寻常光（e）经历的相位变化是（2π／λ）n_eL，于是出射光束通过相位延迟片产生的相位差是：

该相位表示延迟片对全波长的延迟，例如φ＝π是半波延迟，φ＝π／2是四分之一波长延迟。通过光束的偏振态与晶体类型（n_e-n₀）和延迟片的厚度有关。

半波延迟片的厚度L是使电磁波两个正交分量E∥和E⊥的相位差φ＝π，对应波长的一半（λ／2）的延迟，其结果是分量E∥和E⊥相比延迟了180°。此时，如果输入E与光轴的夹角是α，那么输出E与光轴的夹角是-α，输出光与输入光一样仍然是线偏振光，只是反时针旋转了2α。

四分之一波长延迟片的厚度L是使E_∥和E_⊥的相位差φ＝π，对应波长（λ／4）的延迟，其结果是E_∥和E_⊥相比延迟了90°。此时假如0＜α＜45°，那么输出光就不是线偏振光而是椭圆偏振光；假如α＝45°，那么输出光就是圆偏振光。

知识应用：圆偏振和椭圆偏振、石英半波片

例3　例如Ex＝Acos（ωt-kz），E_y＝Bcos（ωt-kz＋φ），A和B不等，φ＝π／2，请问该电磁波是何种偏振？

解　由E_x＝Acos（ωt-kz）得到cos（ωt-kz）＝E_x／A

由E_y＝Bcos（ωt-kz＋φ）得到cos（ωt-kz＋π／2）＝-sin（ωt-kz）＝E_y／B

使用cos²（ωt-kz）＋sin²（ωt-kz）＝1，我们发现

该式表示电场E_x和Ey分量沿x和y轴的瞬时值。当A＝B时，是圆偏振光；当A≠B时，是椭圆偏振光。

当Z＝0，ωt＝0时，E＝E_x＝A；当ωt＝π／2时，E＝E_x＝-B；由此可见该波是右圆偏振光。

例4　石英晶体寻常折射率指数（n₀）是1.5442，非寻常折射率指数（n_e）是1.5533，请问波长λ＝590nm的石英晶体半波片的厚度应该是多少？

解　半波片的相位差φ＝π，代入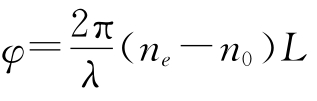，得到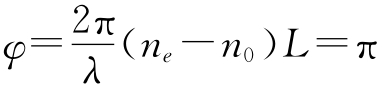，由此可以求得

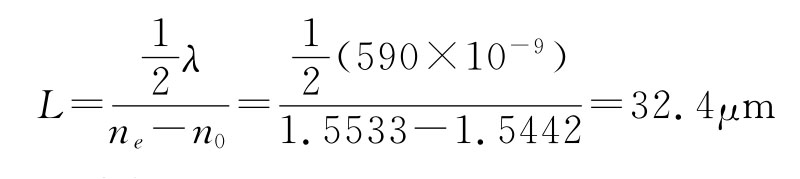
经分析得石英晶体半波片的厚度为32.4μm。

思考题与习题

1.说明线偏振光可用两个旋转方向相反的圆偏振光表示。考虑最简单的沿y轴的线偏振光，从中可以得到什么结论？

2.计算和比较用方解石（n₀是1.658，n_e是1.486）石英晶体制成的四分之一波片的厚度，它们的工作波长均为λ＝590nm，从中有什么结论？假如工作波长是原来的两倍，厚度又是多少？