关系运算与表的操作

3．2．2　关系运算与表的操作

前面已经介绍过，表的操作有四种，它可以分解成六种基本操作：

（1）表的属性指定。

（2）表元组选择。

（3）两个表的合并。

（4）表的查询。

（5）表中元组的插入。

（6）表中元组的删除。

分析这些基本操作后可以发现：这些操作的基本对象都是一个或两个关系，它们经操作后所得的结果仍是关系。因此可以将这些操作看成是对关系的运算，而且满足封闭性。而关系是n元有序组的集合，因此，可以将关系操作看成是集合的运算。

下面讨论这些基本操作是些什么运算。

（1）插入。设有关系R插入若干有序组，这些有序组组成关系R′，由传统集合论可知，可用集合并运算表示，即可写为：

（2）删除。设有关系R删除一些有序组，这些有序组组成关系R′，由传统集合论可知，可用集合差运算表示，即可写为：

（3）修改。修改关系R内的有序组内容可用下面方法实现：

设需修改的有序组构成关系R′，则先作删除，得：

设需修改后的有序组构成关系R″，此时我们将其插入，从而得到结果：

（4）查询。无法用传统的集合论方法去表示用于查询的三个操作，从而要引入一些新的运算。

①投影（projection）运算。对于关系内的属性指定可引入新的运算，称为投影运算。投影运算是一个一元运算，一个关系通过投影运算（并由该运算给出所指定的属性）后仍为一个关系R′。R′是这样一个关系，它是R中投影运算所指出的那些域的分量所组成的关系。设R 有n个域：A₁，A₂，…，A_n，则在R上对域A_i1，A_i2，…，A_im（A_ij∈｛A₁，A₂，…，A_n，｝）的投影可表示成为下面的一元运算：

例3．5　对表3．1所示的关系S有：

∏_sn，sa（S）＝｛（王诚，21），（徐一飞，22），（李峰，20），（赵建平，18），（申桂花，21）｝

∏_sn（S）＝｛（王诚），（徐一飞），（李峰），（赵建平），（申桂花）｝

②选择（selection）运算。对关系内元组的选择可引入另一新的运算———选择运算。选择运算也是一个一元运算，关系R通过选择运算（并由该运算给出所选择的逻辑条件）后仍为一个关系。这个关系是由R中那些满足逻辑条件的有序组所组成。设关系的逻辑条件为F，则R满足F的选择运算可写成为：

σ_F（R）

逻辑条件F是一个逻辑表达式，它可以具有αθβ的形式，其中α，β是域变量或常量，但α，β又不能同为常量，θ是比较运算符，它可以是＜，＞，≤，≥，＝或≠。αθβ叫基本逻辑条件；也可由若干个基本逻辑条件经逻辑运算∧（并且）和∨（或者）构成，称为复合逻辑条件。

例3．6　表3．1所示的关系S中找出年龄大于20岁的所有有序组，可以写成为：

σ（_sa＞20）（S）＝｛（13761，王诚，MA，21），（13762，徐一飞，CS，22），（13765，申桂花，MA，21）｝

例3．7　在表S中找出年龄大于20岁且在数学系（MA）学习的学生，可以写成为：

σ（_sa＞20）_∧（_sd＝MA）（S）＝｛（13761，王诚，MA，21），（13765，申桂花，MA，21）｝

有了上述两个运算后，对一个关系内的任意行、列的数据都可以方便地找到，下面举例如下：

例3．8　在表S中查出所有年龄大于20岁的学生姓名，它可以表示如下：

∏_sn，σ_sa＞20（S）＝｛（王诚），（徐一飞），（申桂花）｝

③笛卡尔乘积（cartesian product）运算。对于两个关系的合并操作可以用笛卡尔乘积表示。设有关系R，S，它们分别为n，m元关系，并分别有p，q个有序组。此时，关系R与S经笛卡尔乘积所得的关系T是一个n＋m元关系，它的有序组个数是p×q，T的有序组是由R与S的有序组组合而成。关系R与S的笛卡尔乘积可写为：

R×S

设有如表3．2所示的两个关系R，S，则R与S的笛卡尔乘积T＝R×S可用表3．3表示。

表3．2　关系R，S

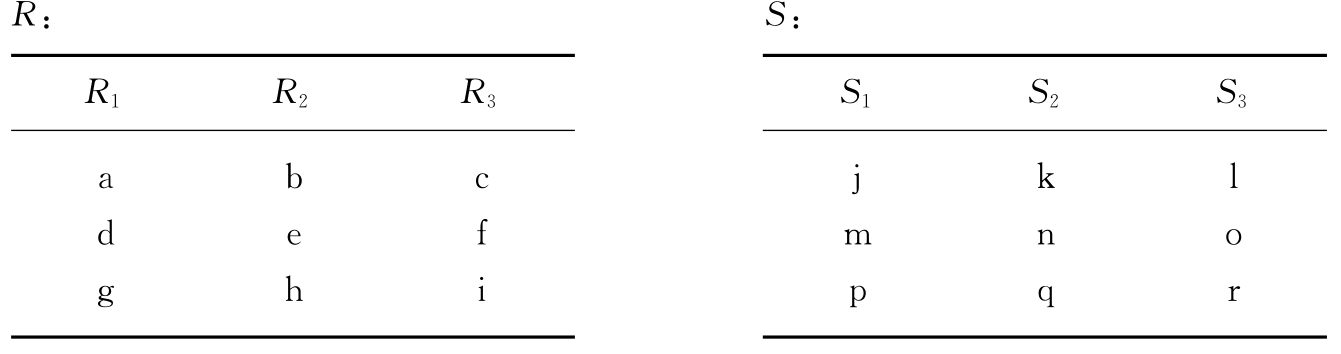
表3．3　T＝R×S

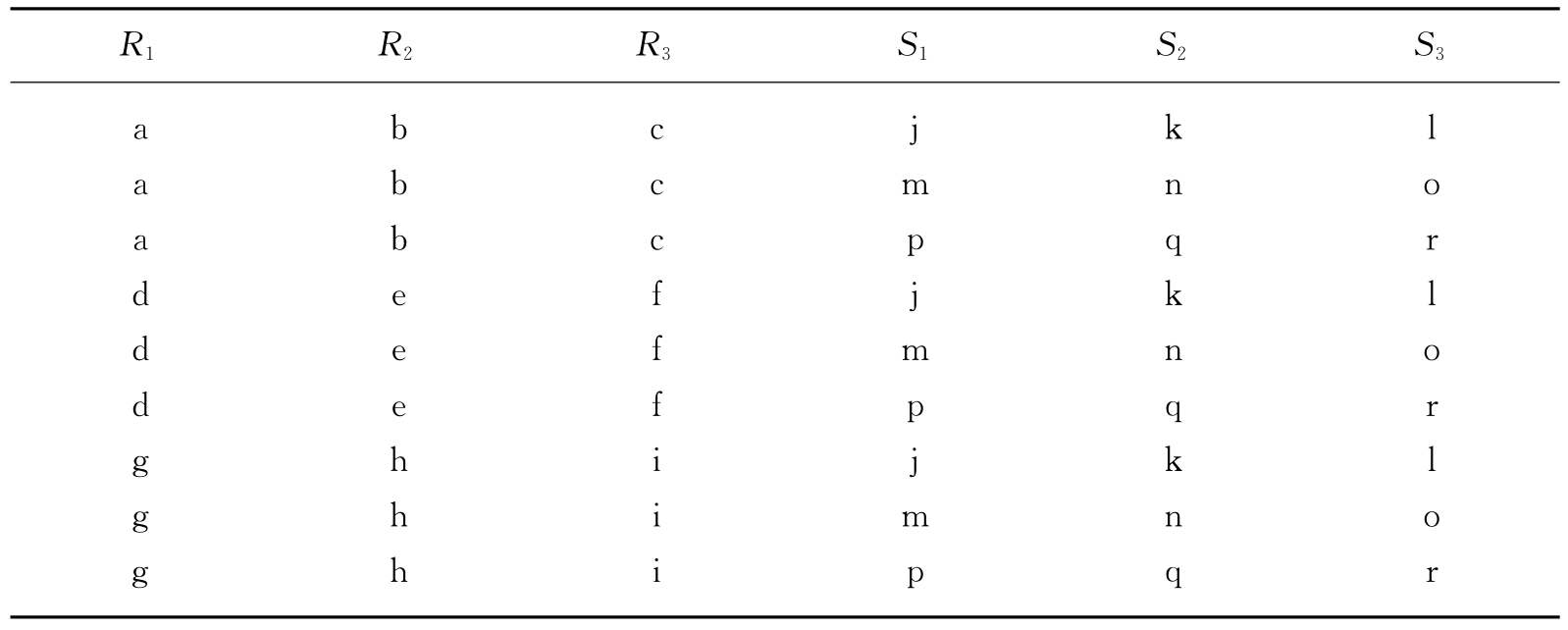
关系代数中上述五个运算是最基本的运算，但为操作方便，还需增添一些运算，特别是用于查询的运算，它们均可由基本运算导出。常用的有联接及自然联接等两种查询运算，现分别介绍如下：

④联接（join）运算

用笛卡尔乘积可以建立两个关系间的联接，但此种方法并不是一种好的方法，因为这样所建立的关系是一个较为庞大的关系，而且也并不符合实际操作的需要。在实际应用中一般两个相互联接的关系往往须满足一些条件，所得到的结果也较为简单。因此，对笛卡尔乘积作适当的限制，以适应实际应用的需要。这样就引入了联接运算与自然联接运算。

联接运算又可称为θ－联接运算，这是一种二元运算，通过它可以将两个关系合并成一个关系。设有关系R，S以及比较式iθj，其中i为R中域，j为S中域，θ为比较符。此时可以将R，S在域i，j上的θ－联接记为：

它的含义可用下式定义：

亦即是说，R与S的θ－联接是R与S的笛卡尔乘积再加上限制iθj而成。显然，的有序组数远远少于R×S的有序组数。

所要注意的是，在θ－联接中，i与j需具有相同域，否则无法做比较。

θ－联接中如θ为“＝”，此时称为等值联接，否则称为不等值联接。如θ为“＜”时称为小于联接，如θ为“＞”时称为大于联接。

例3．9　设有关系R和S分别如表3．4（a）、（b）所示，则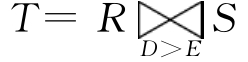为表3．4（c）所示的关系，而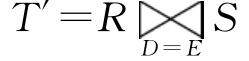为如表3．4（d）所示的关系

表3．4　R与S的θ－联接实例

⑤自然联接（natural join）运算

在实际应用中最为常用的联接是θ－联接的一个特例叫自然联接，这主要是因为常用的两关系间联接大都满足条件：

●两关系间有公共域

●通过公共域的相等值进行联接

根据这两个条件我们建立自然联接运算。

设有关系R、S，R有域A₁，A₂，…，A_n，S有域B₁，B₂，…，B_m，它们间A_i1，A_i2，…，A_ij与B₁，B₂，…，B_j，分别为相同域，此时它们自然联接可记为：

自然联接的含义可用下公式表示：

在此公式中可以看出，自然联接是一种等值联接，其结果关系T的域是由R与S的域所组成，但公共域只出现一次。

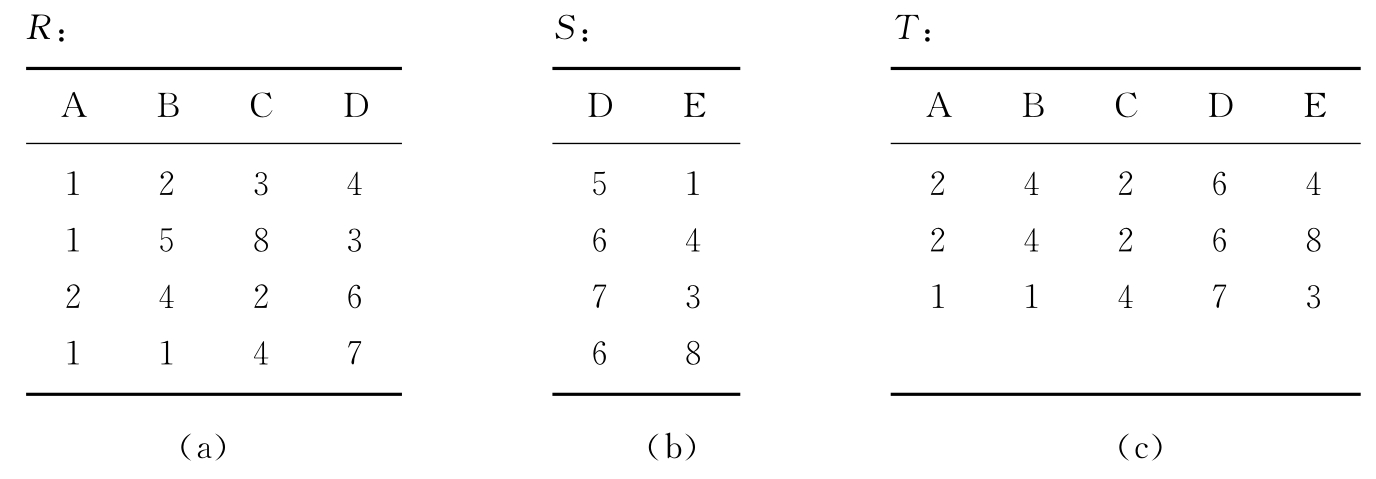
例3．10　设关系R和S如表3．5（a），（b）所示，此时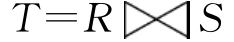则为如表3．5（c）所示。

表3．5　R与S的自然联接实例

至此，引入了五种基本运算与两种扩充运算，一共七种。在这七种最常用的是五种，它们是投影运算、选择运算、自然联接运算、并运算、差运算。一般讲有这五种运算就够了。

到此为止，已经知道关系是一个n元有序组的集合，而关系操作则是集合上的一些运算，其中常用的是五种，它们是：

（1）投影：一元运算，可用∏_A1，_A2，…_Am（R）表示。

（2）选择：一元运算，可用σ_F（R）表示。

（3）自然联接：二元运算，可用表示

（4）并：二元运算，可用R∪S表示。

（5）差：二元运算，可用R－S表示。

这样在关系所组成的集合A上的二个一元运算及三个二元运算，它们满足封闭性条件，其所构成的系统：

（A，∏，σ，，∪，－）

它是个代数系统称之为关系代数。