测量误差的表示方法

2．1．3　测量误差的表示方法

1）绝对误差

绝对误差（绝对真误差）是被测量的测得值与真值之差，可以表示为：

式中：Δ_A为绝对误差；A_x为被测量的测得值；A₀为被测量的真值。

被测量的测得值有较广的范围，包括被测量的实测值，仪器的示值，量具或元件的标称值、预置值，计算的近似值，标准信号源的调定值或定值等。

由于被测量的真值的不可知性，难以通过测量获得，因此，只能用被测量的实际值（或称约定真值）代替被测量的真值。按规定要求，达到误差可以忽略不计，就可以认为该值接近于真值，称之为实际值（或约定／相对真值），可用以代替真值。用比所用仪器的精度等级高一级或数级的仪器的指示值作为被测量的实际值。在测量次数足够多时，仪器的示值的算术平均值作为被测量的实际值。

绝对误差有大小，可正可负，且是一个有单位的物理量，其单位与测得值和实际值相同。其大小和符号分别表示了测量值偏离实际值的程度和方向，但不能表示测量结果的准确度。例如，人体体温在37℃左右，若测量绝对误差为±1℃，这样的测量准确度非常人所能容忍。而如果测量1 400℃左右炉窑的炉温，绝对误差能保持±1℃，这样的测量准确度就相当令人满意了。因此，为了表明测量结果的准确程度，一种方法是将测得值与绝对误差一起列出，如上面的例子可写成37℃±1℃和1 400℃±1℃；另一种方法就是用相对误差来表示。

与绝对误差大小相等、符号相反的量称为修正值C，也叫补值，即

由式（2．2）可见，当测量得到示值后，加上修正值即可消除误差的影响而得到相对真值，即实际值。某些较准确的测量仪器的修正值一般是通过上一级计量部门检定，常以表格、曲线、公式或数字的形式给出修正值。有些自动测量仪器还将修正值预先编成程序存储在仪器中，测量时对测量结果自动进行修正。

例如：由某电流表测得的电流示值为0．83mA，查该电流表检定证书得知该电流表在0．8mA及其附近的修正值都为－0．02mA，那么被测电流的实际值为：

A＝0．83＋（－0．02）＝0．81（mA）

2）相对误差

绝对误差的表示方法一般不便于描述测量结果的准确程度，因此提出了相对误差的概念。相对误差的形式很多，常用的有以下几种：

（1）真值相对误差γ₀

真值相对误差为绝对误差Δ_A与真值A₀的比值，也称为实际值相对误差，通常用百分数来表示：

相对误差只有大小和符号而无单位。这里真值A₀也用约定真值或相对真值代替。但在约定真值或相对真值无法知道时，往往用测量值代替。

（2）示值相对误差（标值相对误差）γ_x

示值相对误差是绝对误差Δ_A与示值A_x的比值，即

应注意，因为示值中也有误差，所以这种表示方法不很严格，在误差比较小时，γ₀和γ_x相差不大，无须区分，但在误差比较大时，两者相差悬殊，不能混淆。

（3）引用误差（满度相对误差）γ_n

一般仪器（仪表）是用来测量某一规定范围的被测量，而不是只测量某一固定大小的被测量。一般仪器（仪表）标尺上各点的绝对误差相近似，而相对误差却随着被测量的减少而逐渐增大；而且有可能增至无限大，因而用相对真误差或示值相对误差不能客观正确地衡量仪器（仪表）的准确程度。

仪器（仪表）的准确度与其本身结构有关。为区分仪器（仪表）的质量等级（该等级通常称为准确度等级），选取仪器（仪表）上限即满刻度值作为参比基准，称为基准值。用绝对误差与基准值的比值来评价仪器（仪表）的质量或测量时的准确度，称为基准误差或引用误差。引用误差是一种简化、实用的相对误差表示方法，常在多挡和连续刻度的仪器（仪表）中应用。

引用误差定义为绝对误差与仪器（仪表）量程之比，用百分数表示如下：

式中：γ_n为引用误差；A_m为测量仪器（仪表）的量程。

对于双向标度尺的仪器（仪表），引用误差定义为绝对误差与测量仪器（仪表）正负两个量限绝对值之和比值的百分数，对于无零位标度尺的仪器（仪表），引用误差定义为绝对误差与测量仪器（仪表）上、下量限之差比值的百分数。

在仪器（仪表）的量程范围内，各示值的绝对误差有正有负，有大有小。所以，确定仪器（仪表）准确度等级时，最大引用误差，即取该仪器（仪表）量程内出现的最大绝对误差ΔA_max，与仪器（仪表）量程Am（满度值）的比值，称为最大引用误差γ_nm，即

式（2．6）中的分子、分母都由仪器（仪表）本身性能所决定，所以最大引用误差可以用来评价仪器（仪表）性能。注意：仪器（仪表）的准确度是指仪器（仪表）在规定的工作条件下可能产生的系统误差。国家标准GB 776—76《电测量指示仪表通用技术条件》规定，电测量仪器（仪表）按准确度等级数a分为：0．1、0．2、0．5、1．0、1．5、2．5、5．0等7级。准确度等级的数值越小，允许的基本误差就越小，表示仪器（仪表）的准确度就越高。准确度等级及所对应的基本误差等于最大引用误差，仪器（仪表）在标尺的全长范围内，其基本误差及最大引用误差都不会超过仪器（仪表）准确度等级指数a的百分数，即

式（2．7）所表明的是其最大引用误差在±a%范围以内，不能误认为在量程内各示值的示值相对误差均在±a%以内。依照上述规定，例如，量程为A_m的a级仪器（仪表），当示值为A_x时，不难得出：电测量仪器（仪表）在使用时所产生的最大可能绝对误差为：

【例2．1】 某电压表a＝1．5，试算出它在0～100V量程中的最大绝对误差。

解：在0～100V量程内上限值A_m＝100V，由式（2．8）得到：

ΔA_max＝a%×A_m＝±1．5%×100＝±1．5（V）

一般说来，测量仪器（仪表）在同一量程不同示值处的绝对误差实际上未必处处相等。但对使用者来说，在没有修正值可资利用的情况下，只能按最坏情况处理。

最大示值相对误差为：

另外，准确度等级a所表示的最大引用误差是在正常使用条件下得出的，如果测量时不能满足规定的工作条件，那么系统误差应包括以准确度等级a所表示的基本误差，再加上工作条件变化时的附加误差。

【例2．2】 最大量限为30A、准确度等级为1．5级的安培表，在规定工作条件下测得某电流为10A，求测量时可能出现的最大相对误差。

解：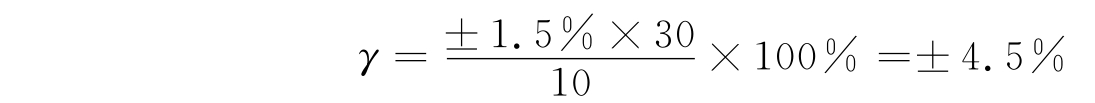

【例2．3】 某1．0级电压表，量程为300V，当测量值分别为U1＝300V，U2＝200V，U3＝100V时，试求出测量值的（最大）绝对误差和示值相对误差。

解：根据式（2．8）可得绝对误差：

ΔU₁＝ΔU₂＝ΔU₃＝±300×1．0%＝±3（V）

γ_U1＝（ΔU₁／U₁）×100%＝（±3／300）×100%＝±1．0%

γ_U2＝（ΔU₂／U₂）×100%＝（±3／200）×100%＝±1．5%

γ_U3＝（ΔU₃／U₃）×100%＝（±3／100）×100%＝±3．0%

由例2．3不难看出：测量仪器（仪表）产生的示值测量误差γ_x不仅与所选仪器（仪表）等级指数a有关，而且与所选仪器（仪表）的量程有关。在同一量程内，测得值越小，示值相对误差越大。应当注意，测量中所用仪器（仪表）的准确度并不是测量结果的准确度，只有在示值与满度值相同时，二者才相等，否则测得值的准确度数值将低于仪器（仪表）的准确度等级。所以，在选择仪器（仪表）量程时，测量值应尽可能接近仪器（仪表）满度值，一般不小于满度值的2／3。这样，测量结果的相对误差将不会超过仪器（仪表）准确度等级指数百分数的1．5倍。这一结论只适合于以标度尺上量限的百分数划分仪器（仪表）准确度等级的一类仪器（仪表），如电流表、电压表、功率表；而对于测量电阻的普通型欧姆表是不适合的，因为欧姆表的准确度等级是以标度尺长度的百分数划分的。可以证明，欧姆表的示值接近其中值电阻时，测量误差最小，准确度最高。

在实际测量操作时，一般应先在大量程下，测得被测量的大致数值，而后选择合适的量程再行测量，以尽可能减小相对误差。

【例2．4】 测量一个约80V的电压，现有两块电压表：一块量程300V，0．5级；另一块量程100V，1．0级。问选用哪一块为好？

解：若使用300V，0．5级表，按式（2．9）求出其示值相对误差为：

若使用100V，1．0级表，其示值相对误差为：

可见由于仪器（仪表）量程的原因，选用1．0级仪器（仪表）测量的准确度可能比选用0．5级仪器（仪表）为高，故选用100V，1．0级仪器（仪表）为好。

此例说明，选用仪器（仪表）时不应只看其准确度等级，而应根据被测量的大小综合考虑其等级与量程，合理选用仪器（仪表）。

（4）容许误差（仪器误差）

容许误差是指测量仪器在使用条件下可能产生的最大误差范围，它是衡量测量仪器最重要的指标。测量仪器的准确度、稳定度等指标都可用容许误差来表征。为了保证测量仪器示值的准确，仪器出厂前和使用期间必须由检验部门对其误差指标进行检验，凡各项误差指标在容许误差范围之内的，视为合格，否则就不合格，其测量结果只能供作参考。

仪器的容许误差的表示方法可以用绝对误差，也可用相对误差。容许误差可用工作误差、固有误差、影响误差、稳定性误差来描述。

①工作误差

工作误差是在额定工作条件下仪器误差的极限值，即来自仪器外部的各种影响量和仪器内部的影响特性为任意可能的组合时，仪器误差的最大极限值。

②固有误差

固有误差是当仪器的各种影响量和影响特性处于基准条件下仪器所具有的误差。由于基准条件比较严格，所以，固有误差便于在相同条件下对同类仪器进行比对和校准。

③影响误差

影响误差是当一个影响量处在额定使用范围内（或一个影响特性在其有效范围内），而其他所有影响量处在基准条件时仪器所具有的误差，如频率误差、温度误差等。

④稳定性误差

稳定性误差是在其他影响和影响特性保持不变的情况下，在规定的时间内，仪器输出的最大值或最小值与其标称值的偏差。习惯上用相对误差表示或者注明最长连续工作时间。