【摘要】：巴特沃斯滤波器的特点是在通频和阻频带内，其幅频特性均没有起伏振荡，即在截止频率ωo左边（通频带）和ωs右边（阻频带）附近域内均为平滑过渡，如图5．26所示。如将多个低阶滤波器级联，可得高阶巴特沃斯有源RC滤波器。由于每个低阶滤波器均引入了电压负反馈，故具有极低的输出阻抗。
5．2．4 巴特沃斯滤波器
1）基本巴特沃斯滤波器
巴特沃斯（Butterworth）滤波器的特点是在通频和阻频带内，其幅频特性均没有起伏振荡，即在截止频率ωo左边（通频带）和ωs右边（阻频带）附近域内均为平滑过渡，如图5．26所示。
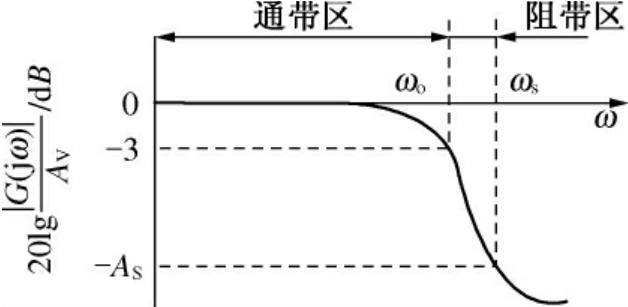
图5．26 巴特沃斯滤波器幅频特性
图5．27是一个二阶巴特沃斯滤波器。
（1）低通滤波器
对于图5．27（a）所示的低通滤波器，其传递函数为：
式中：ζ为阻尼比，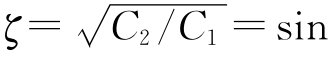
（π／4）；ωn为电路无阻尼自振频率（固有频率），ωn＝1／
。
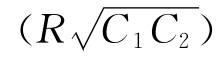其幅频特性为：
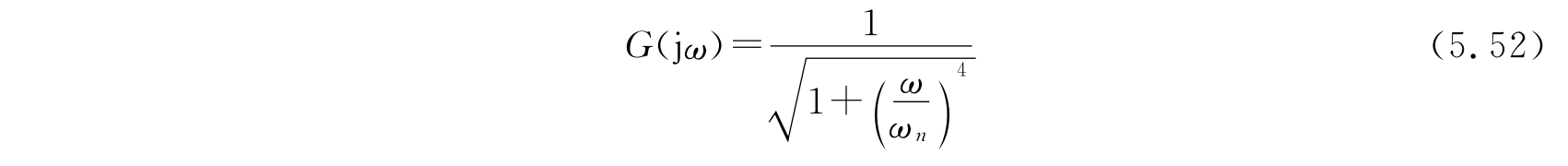
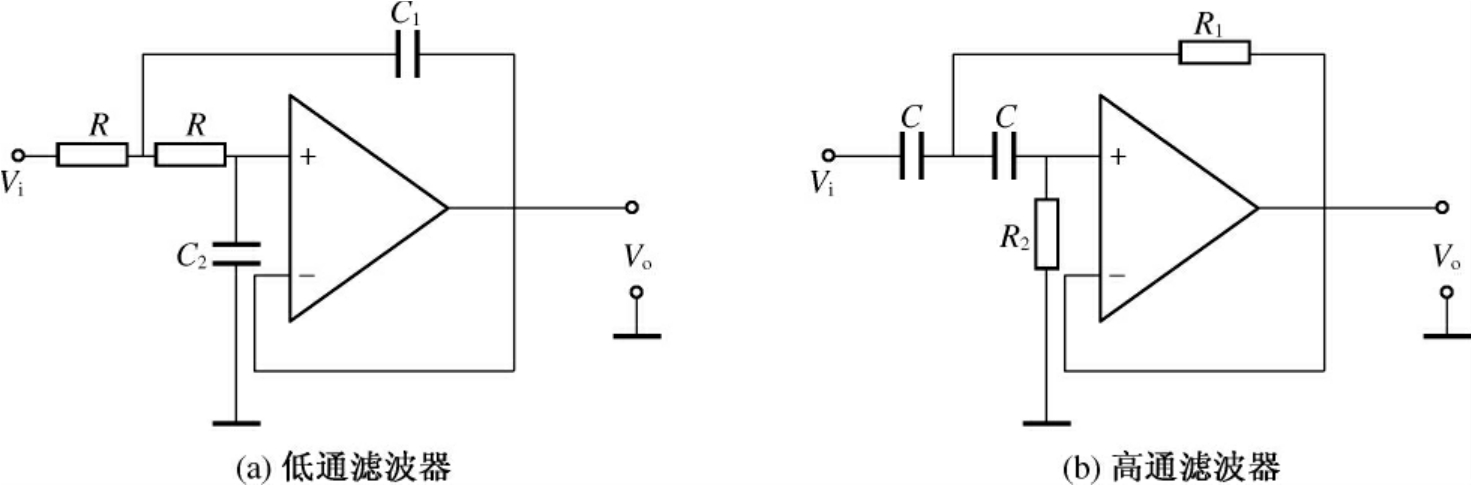
图5．27 二阶巴特沃斯滤波器电路
（2）高通滤波器
对于图5．27（b）所示的高通滤波器，其幅频特性为：
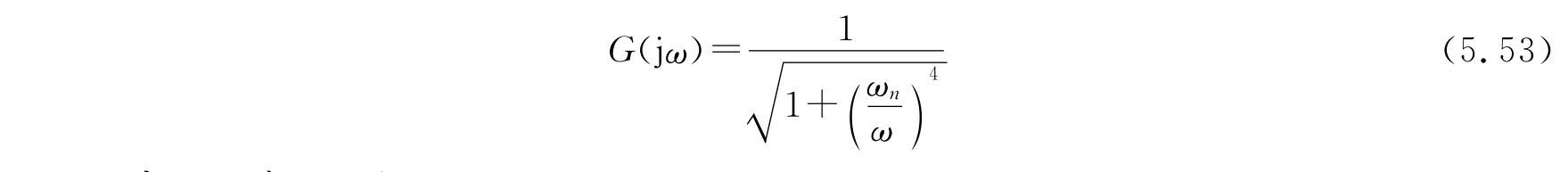
2）高阶巴特沃斯滤波器
如将多个低阶滤波器级联，可得高阶巴特沃斯有源RC滤波器。由于每个低阶滤波器均引入了电压负反馈，故具有极低的输出阻抗。级联后高阶滤波器的传递函数等于各低阶滤波器传递函数的连乘，其传递函数为：
n为偶数时，
n为奇数时，
式中：n为阶数；k为级联滤波器个数；ζk为各滤波器阻尼比，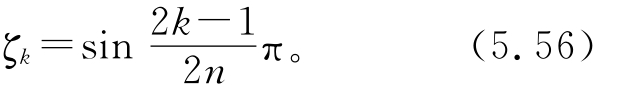
当P＝ωn／s时，G（s）为高通滤波器传递函数；P＝s／ωn时，G（s）为低通滤波器传递函数。
图5．28为一个六阶低通巴特沃斯滤波器，当其满足条件：
（1）ωn1＝ωn2＝ωn3＝ωn，即
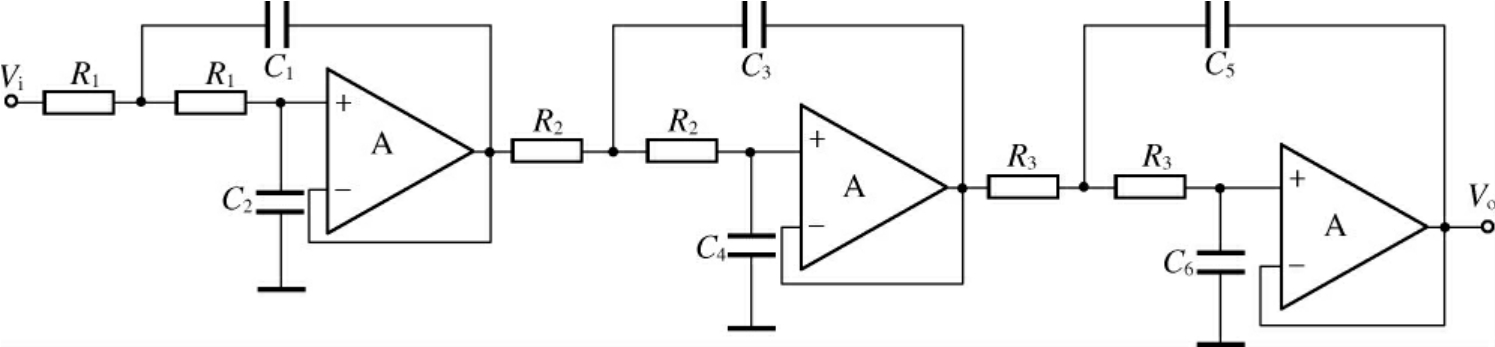
图5．28 六阶低通巴特沃斯滤波器电路
（2）ζ1、ζ2、ζ3满足式（5．56）时，即
其幅频特性为：
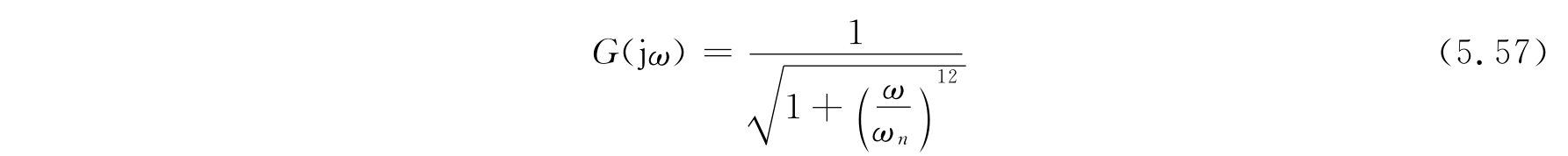
一般说来，高阶滤波器的滤波性能优于低阶滤波器，其陡度（对通带之外频率干扰信号的抑制程度）高于低阶滤波器。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
