加工误差的统计分析

2.6　加工误差的统计分析

前面已经对加工精度的各种因素进行分析，并提出解决问题的一些方法。但就其分析方法来说，还是属于局部的、单因素的性质。而在实际生产中，对加工精度的影响因素是很复杂的，很难用前述单因素的估算方法来分析其因果关系，而需要用概率统计方法进行综合分析，才能找出解决问题的途径。

2.6.1加工误差的性质

各种工艺因素的加工误差，按其性质，即根据加工一批工件时误差出现的规律，可以分为系统性误差和随机性误差两大类。

1）系统性误差

在顺序加工一批工件时，若误差的大小和方向保持不变，或按一定规律变化，即为系统性误差。前者称为常值系统性误差；后者称为变值系统性误差。例如，量具的对零误差、铰孔时铰刀的直径误差等，属于常值系统性误差。工艺系统的热变形、刀具的磨损等引起的误差，属于变值系统性误差。

2）随机性误差

在顺序加工一批工件时，若误差的大小和方向呈无规律变化，这类误差称为随机性误差。毛坯误差的复映、定位误差、内应力引起的误差、多次调整的误差等，都属于随机性误差。

对于常值系统性误差，在掌握其大小和方向后，就可以通过调整或补偿等方法来消除。对于变值系统性误差，在掌握其变化规律后，则通过采取自动连续补偿或自动周期补偿来消除。而对于随机性误差，由于它没有明显的变化规律，所以只能通过数理统计方法找出其统计规律，采取措施减少影响。

2.6.2　分布曲线分析法

分布曲线分析法是从某一工序所加工出来的工件中，随机抽取足够数量的一批工件，对所要分析的精度指标（尺寸）进行测量，作出分组数据表和分布曲线，再运用数理统计学原理来推断该工序的加工精度状况。

1）实际分布曲线

从随机抽取的一批工件中，测量每个工件的加工尺寸，把测得的数据记录下来，按尺寸大小把整批工件进行分组，则每一组中的零件尺寸处在一定的间隔范围内。同一尺寸间隔内的零件数量称为频数，频数与该批零件总数之比称为频率。以零件尺寸作为横坐标，以频率作为纵坐标，便可得到实际分布曲线。

例如，检查一批精镗后的活塞销孔直径，图样所规定的尺寸为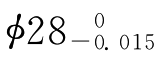，检查件数为100件，把测量所得的数据按尺寸分成6组，每组的尺寸间隔为0.002mm，然后填在表2.2中。表中n是测量的工件数，m是每组的件数。

表2.2　活塞销孔直径分布

以工件中点尺寸x为横坐标，以频率m／n为纵坐标，便可画出实际分布曲线图（图2.31）。图中虚线所示为理想分布位置，实线为实际分布位置。在图上再标出公差带及其中心、实际尺寸的分散范围及其中心，便可对加工质量进行分析。

分散范围＝最大孔径－最小孔径＝28.004－27.992＝0.012（mm）

系统性误差Δ_系统＝27.997 9－27.992 5＝0.0054（mm）

图2.31　活塞销孔直径尺寸分布曲线

分散范围与分散范围中心可表达这批工件的加工情况，现分析图2.31中的分布曲线：

（1）分散范围小于公差带，即0.012＜0.015，表明本工序能满足加工精度要求。

（2）废品率占18%（28～28.004），其原因是尺寸分散范围中心与公差带中心不重合，存在系统性误差为0.005 4mm，所以只要把镗刀伸出量减少0.005 4／2＝0.002 7mm，使分散范围中心与公差带中心重合，即可解决这批工件的加工质量问题。

2）正态分布曲线

在绘制一批工件的分布曲线图时，若所取的零件数量增多而尺寸间隔减小，则所绘出的图形非常接近光滑的曲线——理论分布曲线。

常用的理论分布曲线是正态分布曲线。这是因为在机床上用调整法加工时，如果加工过程中情况正常，则加工出的一批工件的尺寸分布曲线符合正态分布曲线。

正态分布曲线的方程式为

当采用正态分布曲线来代替加工尺寸的实际分布曲线时，式中的符号分别表示如下：

x——工件尺寸；

－x——工件平均尺寸（分散范围中心）；且有

n——一批工件的总数；

σ——标准差；且有

正态分布曲线的图形如图2.32（a）所示。从该图形上可看出下列特点：

图2.32　正态分布曲线的性质

（1）曲线以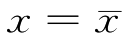直线为轴左右对称，靠近的工件尺寸出现概率较大；远离的工件尺寸出现的概率较小。

（2）工件尺寸对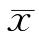的正偏差和负偏差的概率相等。

（3）分布曲线与横坐标所围成的面积包括了全部零件数，故其面积等于1；其中＝±3σ（即在x－±3σ）范围内的面积占99.73%。即有99.73%的工件尺寸在±3σ范围内，仅0.27%的工件在范围之外。因此，取正态分布曲线的分布范围为±3σ（或6σ）。

±3σ是一个很重要的概念，在研究加工误差时应用很广。通常用6σ的大小代表某一种加工方法在一定条件下所能达到的加工精度。所以，在一般情况下应使公差带的宽度T和所选择的加工方法的标准差之间具有下列关系：

6σ≤T

但考虑到变值系统性误差及其它因素的影响，总是使公差带的宽度T大于6σ，才能保证加工精度。

（4）标准差σ是决定分布曲线形状和尺寸分散范围的参数，σ越大曲线越平坦，尺寸越分散，也就是加工精度越低；σ越小曲线越陡直，尺寸越集中，也就是加工精度越高，如图2.23（b）所示。σ的大小受随机误差的影响。

3）非正态分布曲线

工件的实际分布状况，有时并不符合正态分布，常见的分布形状有：

（1）双峰形

当将两次调整下加工出的工件混在一起测量时（混批），分布曲线将呈双峰形（图2.33（a））。它实质上是两组正态分布曲线的叠加，也就是在随机误差中混入了常值系统性误差——调整误差。

图2.33　非正态分布曲线

（2）平顶形

当存在一个非正态分布的优势误差因素时，例如，砂轮磨损较快时，尺寸分布曲线将呈平顶形（图2.33（b））。它实质上是正态分布的尺寸分散中心在不断移动。这是一种在随机性误差中混有变值系统性误差的情况。

2.6.3　点图分析法

应用分布曲线法，由于没有考虑到工件的加工顺序，所以不能区分变值系统性误差和随机性误差。又由于是一批工件需加工后才能绘制分布曲线图，因此不能在加工过程中提供控制工艺过程的资料。为了弥补分布曲线法的上述缺点，在生产实际中采用点图分析法。点图有各种形式，应用最广的是点图。

1）点图

以分组序号为横坐标，每组零件的平均尺寸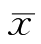为纵坐标，即可绘出点图。该点图可看出尺寸的变化趋势，突出变值系统性误差的影响。

再以分组序号为横坐标，以每组零件的极差R（组内工件的最大尺寸与最小尺寸之差）为纵坐标，绘出的点图叫“极差R点图”，简称R图。该点图主要用来显示加工过程中尺寸分散范围的变化情况。

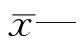在分析问题时图和R图常联合使用，因此称为 R点图，如图2.34所示。

图2.34　—R点图

2）点图法的应用

（1）从图上可观察出变值系统性误差和随机性误差的大小及变化情况；

（2）判断工艺过程的稳定性及工艺能力（提供工艺验证资料）；

（3）提供控制工艺过程的资料，根据工件在加工过程中尺寸变化趋势，决定调整机床的时间，以实现产品的质量控制。

3）验证工艺过程的稳定性

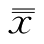用点图验证工艺过程的稳定性时，需在图上画出其中心线及上下控制线，而控制线就是判定工艺稳定性的界限线。如图2.35所示，在x－图中，中心线是的平均数线是上控制线是下控制线。在R图中，一般只标上控制线R_u，不标下控制线。

图2.35　用图验证工艺稳定性

各线的位置分别按下列公式计算：

式中的系数A和D可按表2.3选取。一般情况下，每组件数m取4或5。

表2.3　A与D系数表