两级共源放大器频响特性

8．4　两级共源放大器频响特性

增益级水平级联的电路结构是另一种提高电路直流增益的常用方式，它引入的极点无法确保相互间一定为分离的极点。与此相反，在Cascode垂直级联中，CG管的输出阻抗与负载电容既为A₁的零点，又为A₂的极点，两者相互抵消，输出的极点被压缩，而中间级的极点被扩展，产生的一定是分离的极点。一般而言，单级放大器只存在一个高阻极点，输入极点在理想电压源驱动下是一个远大于GBW带宽的高频极点，因此单级放大器通常不存在稳定性问题，而且相位裕度PM＞90°。但对于多极点系统，当极点频率相互接近时，必然带来系统稳定性方面的问题。

多级增益电路结构决定了多级放大器必定存在多个高阻低频极点。多级放大器多种不同的组合模式，决定了极点之间不同的位置关系。高阻输出的CS增益结构具有较低的极点频率和相对较差的频率特性，CD由于输出低阻、CG由于消除了Miller电容效应，因而具有相对优良的频率特性。多级增益结构频率特性设计的难点在于因存在闭环系统稳定性方面的问题，CS电压增益的级联必须根据电路具体的频率特性，提出相应的频率补偿方法。

两级放大器是多级放大电路中最简单的电路形式，起承上启下的作用，并且采用的分析方法和相关结论可以推广到多级电路的分析。本章重点讨论两级放大器的频率响应特性，并提出两级电压放大器频率补偿的基本原则。

为求简化，以理想电压信号激励下两级CS电压放大器频率响应为例，对其动态过程进行全面的物理分析，电路如图8－19所示。当没有外接补偿电容时，本征Miller电容C_M＝C_GD≈0。

作为第一级增益，差分输入级的主要设计要求包括：大的L以减小差分对失调，提高输出阻抗，高的输出阻抗以提高增益、较低的静态偏置电流以降低功耗；第二级增益即输出级的要求为：较大的静态电流以提高大信号摆率SR，获得适中的输出阻抗和电压增益。

图8－19　两级OTA电路

根据以上两级增益电路设计的一般要求，选取跨导g_m1＝50μS、g_m2＝0．5mS、输出导纳g_o1＝0．1μS、g_o2＝10μS、结点电容C₁＝1pF、C₂＝3pF，并以此为例分析未补偿两级增益的频率特性。

两级增益的低频直流增益为

总的低频直流增益近似为A_V0＝A₁A₂≈88dB，两极点位置及对应的极点频率为

在分析电路幅频和相位变化过程中，p₁A_V0＝400MHz》f₂，虽然f₂的作用使实际的GBW＜p₁A₀，但仍然满足GBW》f₂的条件，则GBW下的总相位移达到180°，系统因正反馈而失去稳定。因此，采用基本Miller电容补偿策略。

在Miller电容压缩下，其主极点位于第一级的输出，即

Miller电容除了压缩主极点的作用外，还由于C_M电容等效GD短路作用而使输出极点扩展为p₂＝g_m/C_L。

如进一步考虑C_M电容引起的RHP零点，忽略理想电源激励下的高频输入极点，则两级系统电压增益传递函数可近似表示为

根据电路Bode图描述的频率特性，可判断电路的稳定性，对于可能出现的不稳定状态，可以根据频率补偿的原理选择相应的实现方式。频率分析的过程主要分为以下3个主要频段

（1）低频段

对于低频直流增益A₁₀＞A₂₀的两级开环运放电路，根据以上计算结果，即使在没有Miller电容补偿的条件下，只要输出级驱动电容较大，且负载电容不过大，则－3dB主极点一般均位于第一级的输出。因此A₁首先随频率开始下降，当A₁下降到A₂₀的幅值时，对应于信号频率的低频频段。对于A₂，其各结点电容容抗均远大于该结点位置下的输出阻抗，电容不起作用，A₂表现为低频常数A₂₀。因此，A₁的－3dB点，也就是整体电路的－3dB点，在该点处A₁贡献的相位迟滞为45°。若A₁₀/A₂₀＞10，则到达A₁＝A₂₀低频区的临界点时，A₁贡献的总相移近似达到90°饱和值，低频条件下的幅频和相频特性如图8－20所示。

图8－20　低频段两级增益的频率特性

在低频条件下，由于次级A₂增益保持为较高的常数状态，Miller电容效应起作用，根据补偿电容C_M中的电流，得到的等效输入电容值为

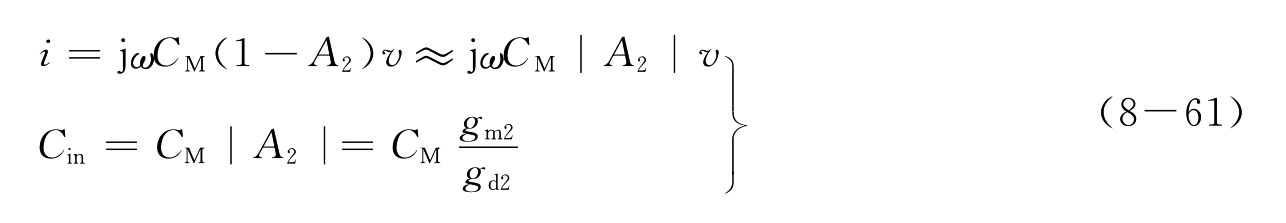
根据C_M＝3pF、｜A₂₀｜＝50的条件，等效输入电容C_in＝150pF，而原来的负载电容仅为C₁＝1pF，对应于主极点压缩150倍，即p₁＝15．9k/150＝106Hz。

（2）中频段

中频段，A₁继续保持－20dB/dec的增益下降速率，A₂保持一段常数后，当到达p₂极点频率位置时开始下降。在次频率点下A₂贡献的相位迟滞为45°，该状态下总相位移最大可为135°。总增益视前后两级增益在此频率下的值，可大于1，也可小于等于1。对于本电路，直至下降到总增益为0dB时结束中频区域。

在此频段，虽然A₂略有下降但仍然保持一定的增益值，因此对Miller电容起倍增作用的A₂增益基本保持不变，等效负载电容为C_M＋C₂，而且在此频率范围内输出容抗值已开始小于输出阻抗，才能实现A₂随频率增加而单调下降的特性，因此有A₂＝－g_m2/［jω（C_M＋C₂）］。

在此条件下，由于A₂》1，则Miller电容等效到输入端的注入电流为

则Miller电容在此频段可等效为A₂的输入阻抗，即R_in＝V/i＝（1＋C₂/C_M）/g_m2＝（1＋1）/（500×10_－6）≈4kΩ。

该电阻可并入第一级的输出阻抗，由于该阻抗很小，大幅度降低了A₁在此频段的输出阻抗，抑制了负载电容效应，使A₁随频率提高而衰减的速度减缓。同时相位迟滞开始减小，表现为超前特性，再加上P₂极点的相位迟滞，总的相位保持缓慢的变化。此外，通常认为在超出p₂频率点后，A₂以－20dB/dec频率下降，A₂的0dB增益点所对应的频率为g_m2/（C₂＋C_M），则总增益以－40dB/dec速率下降。考虑到A₁下降的减缓效应后，系统增益－40dB/dec的下降起始点p₂比A₂的－3dB点略有增加，此频率内的频率响应特性如图8－21所示。

图8－21　中频段两级增益的频率特性

（3）高频段

在高频阶段，仅由电容决定各级增益的负载，因此A₁、A₂均随频率的增加而下降。高频下C_M可视为短路，因此很难在低频下分开考虑A₁和A₂的作用，而需整体考虑。由输入—输出结点方程的推导，即g_m1v_in＋sC₁V＝（V_o－V）sC_M，（V_o－V）sC_M＋g_m2V＝－sC₂V_o，可得

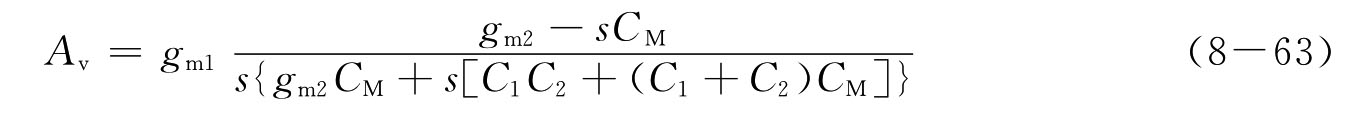
代入s＝jω，得到高频下增益的频率响应特性为

Miller电容引起的RHP零点频率为z＝g_m2/（2πC_M）≈500μS/（2π·3pF）＝26．5 MHz。高频LHP次极点频率为

单位增益带宽相对于没有Miller补偿的条件，下降到GBW＝Af₁＝g_m1/（2πC_M）＝2．65MHz。

显然，NDP＝p₂/GBW＝6、NZ＝z/GBW＝10，高频次极点和RHP零点均远在GBW外，相位裕度至少可达到60°。此频率内的频率响应特性如图8－22所示。

图8－22　高频段两级增益的频率特性

图8－23给出了基本Miller电容补偿控制前后两级增益p₁、p₂极点的原理示意图，采用Miller电容补偿的条件为原始未补偿下的极点满足p₁＜p₂的关系，即g_o2/C₂＞g_o1/C₁。为此第一级应为高阻增益级、第二级应为负载电流驱动级，且C₂电容较低。经过Miller电容补偿后小的p₁极点被压缩、而大的p₂极点进一步扩展，实现主次极点的分离，补偿效果明显。而对于电路负载电容C_L＝C₂很大，或输出级阻抗及增益很大的状态，本征极点p₂大幅度下降，Miller电容补偿的效果减弱甚至失效，此时需要采用新的补偿策略。

对比Cascode和Cascade两种提高增益的基本电路结构，Cascode具有比Cascade更加优越的频率特性。在以上两种方式之外，还存在一种增益倍增型（Regulated Cascode）结构，该类型电路是对Cascode结构的进一步改进，即采用附加的增益A_V3提高输出阻抗，以提高总体增益，虽然主极点频率进一步下降，但保持GBW近似不变，并且确保各次极点频率位于GBW外，以实现多级增益的单极点系统低频特性，其幅频特性近似如图8－24所示。有关增益倍增型Cascode的电路设计详见第10章。

图8－23　主次极点分离的Miller电容补偿

图8－24　增益提高型Cascode频率特性