小信号瞬态特性

10．2　小信号瞬态特性

高速运放在音频、视频信号的实时采集和处理系统中有广泛的应用。所谓高速通常包含两方面的含义，首先是运放的带宽足够宽，能够不失真地处理高频或宽带输入信号。带宽问题是一种线性处理的小信号问题，涉及系统闭环下的稳定性。应采用合适的频率补偿结构，在保证系统稳定的前提下尽可能扩展运放的带宽。高速运放的另一个含义是指输出对输入的高速度响应，即响应时间应尽可能短。运放的瞬态响应包含了大信号与小信号响应两个方面，小信号瞬态响应与系统带宽相联系，此时高速与带宽的要求相吻合。而大信号瞬态响应则与输出负载电容充放电的压摆率SR相关，此时高速与大负载电容的驱动能力要求相吻合。

由于各类运放均工作于闭环负反馈状态，因此最终归结为闭环系统的带宽和瞬态响应速度性能。闭环系统的瞬态响应与开环运放的瞬态特性及负反馈结构密切相关。在以下讨论中，以基本电压放大器为例，首先分析开环系统的瞬态响应，在此基础上分析闭环瞬态特性与开环结构的关系。同时，在瞬态响应的分析中，区分小信号与大信号的不同驱动作用。

10．2．1　一阶系统小信号瞬态特性

1）一阶开环零－极系统

首先考虑一个零点和一个极点的开环系统，其归一化传递函数G（s）/G₀＝（1＋s/z）/（1＋s/p）。在1（t）单位阶跃激励下，由于L［1（t）］＝1/s，则开环归一化输出的瞬态时域输出为

式中，V_swing＝G₀V_step，为输出信号的最大电压摆幅。

代入t＝0时的归一化初始值V_o（t₀）＝p/z。零点可正、可负，对输出的收敛性没有影响，但对初始状态有影响。只有极点影响瞬态输出的收敛性，因此所有极点必须具备LHP性质。当零点远大于极点频率时，如对于无穷远零点，则零点的作用可消除，此时输出只与极点有关，即

V_o（t）/V_swing＝1－exp（－pt）　　　　　　　（10－2）

在LHP零点等于LHP极点的条件下，零—极点完全相消，输出V_o（t）＝V_swing为恒定常数，即不存在瞬态变化项，瞬态响应不存在延迟。由于参数漂移将导致零点在极点附近变化，理想的零—极补偿发生偏差。此时，输出响应的瞬态项重新显现，但其系数很小。这种相互靠近的零极点称为偶对，偶对对于相位移的影响可以忽略，而对瞬态项的影响则无法完全消除。两者的匹配程度越高，瞬态响应项的系数越小，瞬态响应速度越快。当零点为RHP性质时，不但造成相位特性退化，同时导致输出瞬态项系数增加，使输出响应的瞬态性能严重下降。

在只有极点存在的前提下，输出与理想值的相对误差为exp（－pt），系统主极点p是决定瞬态响应性能的主要因素。在相同的时间内，主极点频率越高则误差越小，或者说达到相同的误差条件对于高频主极点所需的时间越短，瞬态响应速度越高。

2）一阶闭环零—极系统

对于单极点和单零点开环增益通过反馈网络F构成的闭环负反馈系统，其闭环传递函数A_CL＝G（s）/［1＋F·G₀（s）］可表示为

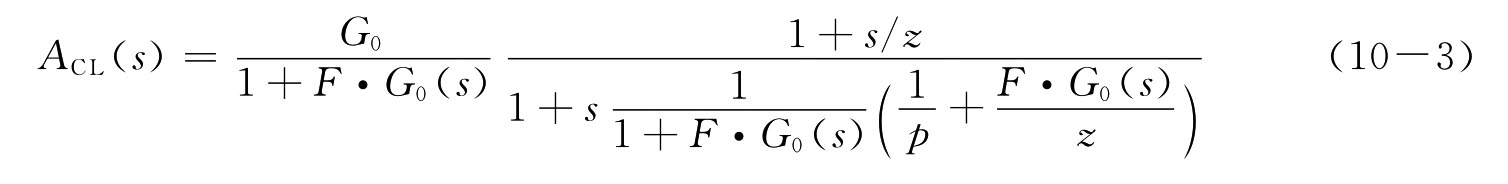
式中，A_CL（0）＝G₀/（1＋F·G₀（s））为低频直流下的闭环增益，当F＝0时，则A_CL（s）退化为原来的开环A（s）。

考虑到高的低频开环增益F·G₀（s）》1的条件，上式可简化为

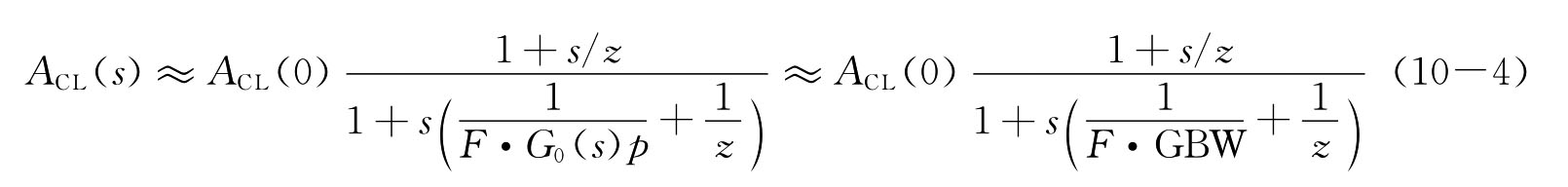
开环系统的零点在闭环中保持原来的性质和状态不变，z_c＝z，而极点则受开环极点、零点和直流增益的共同影响。在LHP零点作用下，闭环极点频率为

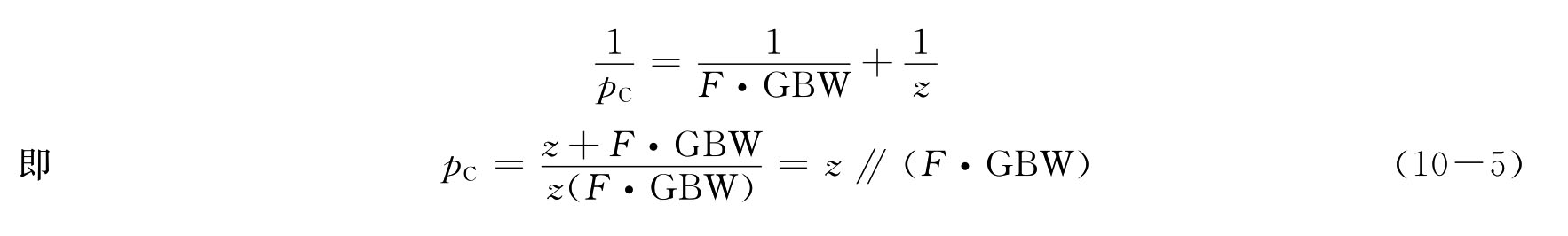
因此，代入闭环的零极点后，单位阶跃1（t）激励下瞬态响应输出关系对闭环同样适用。在z》GBW的条件下，零点的作用可以忽略，则闭环系统的归一化瞬态输出为

V_o（t）/V_swing＝1－exp（－F·GBW·t）　　　　　　　（10－6）

同样，对于闭环系统，环路的单位增益带宽越大，响应时间越短，速度越快。提高速度的根本措施，一是降低负载电容，二是降低本征电阻，电阻降低使得输出电流驱动能力增强，最终实现宽GBW。

10．2．2　两阶系统小信号瞬态特性

两阶系统有两种，即一阶增益或两阶增益系统。一阶增益系统中极点的一般表达式为p＝g_m/C_L。在高频下，考虑g_m管极间电容C_gd对电流的分流作用，跨导不再是常数。将高频管等效成低频管，其等效跨导为G_m，则G_mV_i为经地反向流入等效负载R_L，eff的电流，考虑到｜V_o｜》｜V_i｜，则

G_mV_i＝g_mV_i＋（V_o－V_i）sC_gd≈g_mV_i＋V_osC_gd＝g_mV_i－G_mV_iR_L，effsC_gd　　　　　　（10－7）

实际输出阻抗仍与频率有关，等效阻抗为

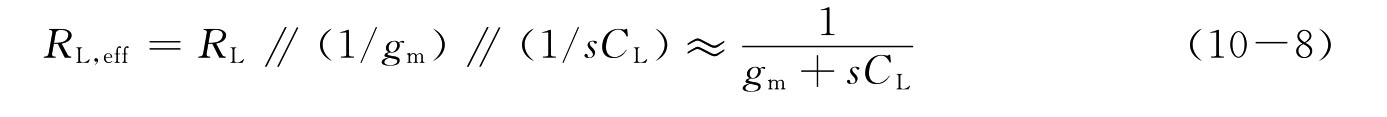
高频下的等效跨导退化为

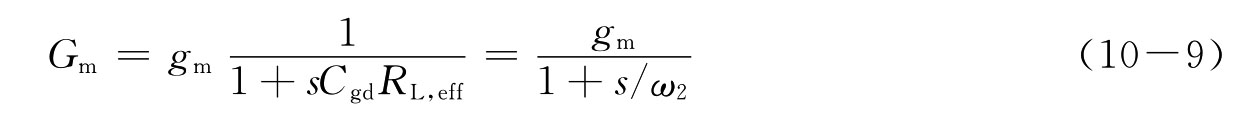
G_m随频率的增加而减小。对于单级闭环增益，在输出极点频率ω₁＝g_m1/C_L，eff的条件下，考察G_m变化对频率特性的影响，由于

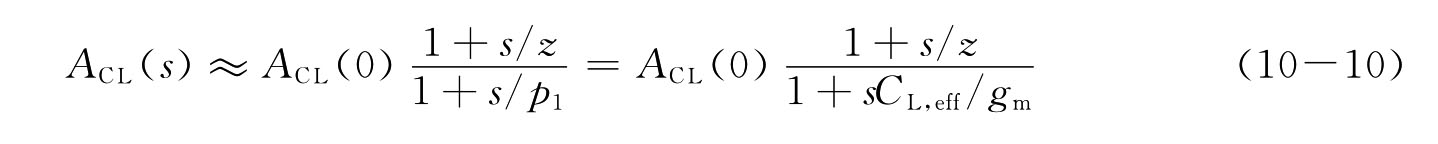
将上式中的g_m由G_m取代，由此得到高频下C_gd寄生电容效应对开环的影响

对应的ω₁＝g_m/C_Leff，ω₂＝g_m/C_gd，上式还可以表示成标准的二阶形式

式中ω₀²＝ω₁ω₂，ζ＝ω₀/（2ω₁），Q＝1/（2ζ）。由于ω₂》ω₁，因此对于一级增益考虑寄生效

应得到的两个极点，其中次极点是高频极点，其影响很小。对于两级增益系统，忽略高频寄生电容效应的影响，一定是两极点系统，同样可用上式表示，只是ω₁、ω₂频率点的变化而已，并且两个极点可以是分离的实极点，也可以是共轭复极点。若考虑高频寄生效应，则极点因子增加到ω₁、ω₂、ω₃，只有z》GBW才能忽略零点的影响。

对于一般形式（闭环或开环）的两极点系统，由于极点的不同分布类型，在阶跃激励下，下面分2种不同的极点状态讨论其瞬态输出响应。

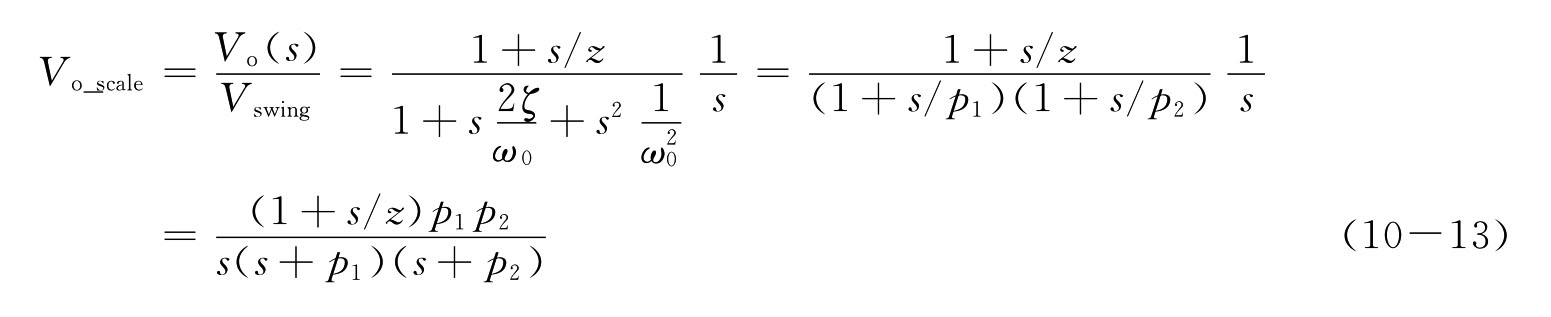
1）ζ＞1或Q＜1/2条件

以上条件对应于两分离的实极点状态，则

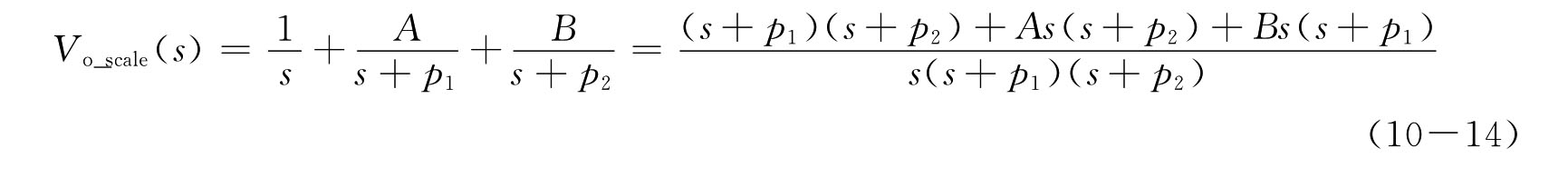
整理后，有

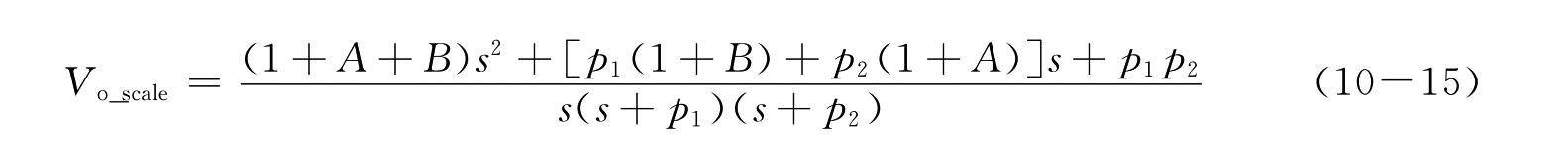
对比同类项系数，得

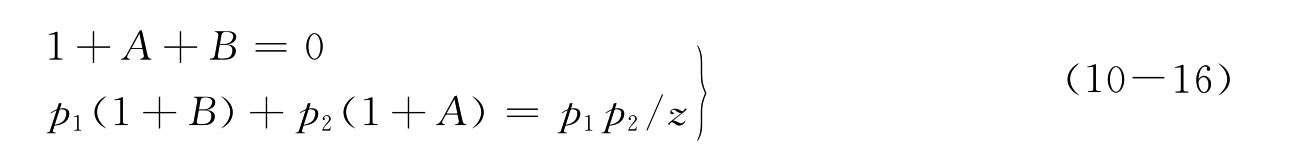
显然，零点的存在将改变A、B系数。两实极点分别为

在z→∞并可忽略零点作用的前提下，仅考虑两极点的作用，解得的待定系数A、B分别为

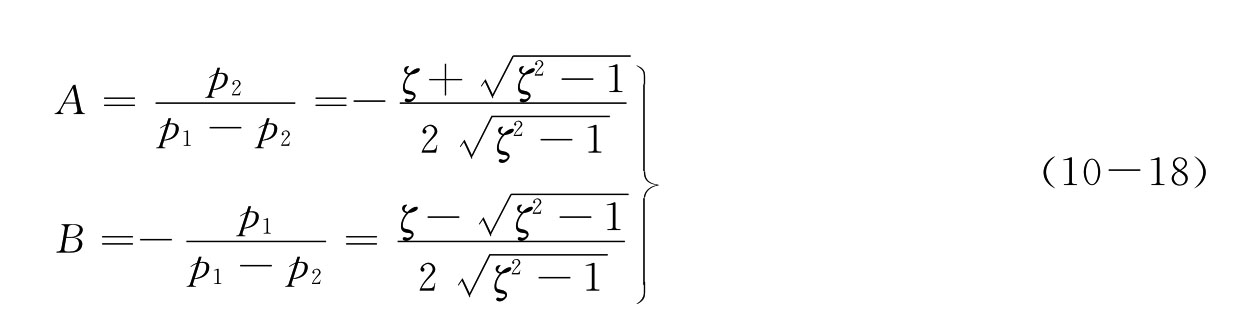
则由拉氏反变换得到分离实极点状态下的归一化瞬态响应为

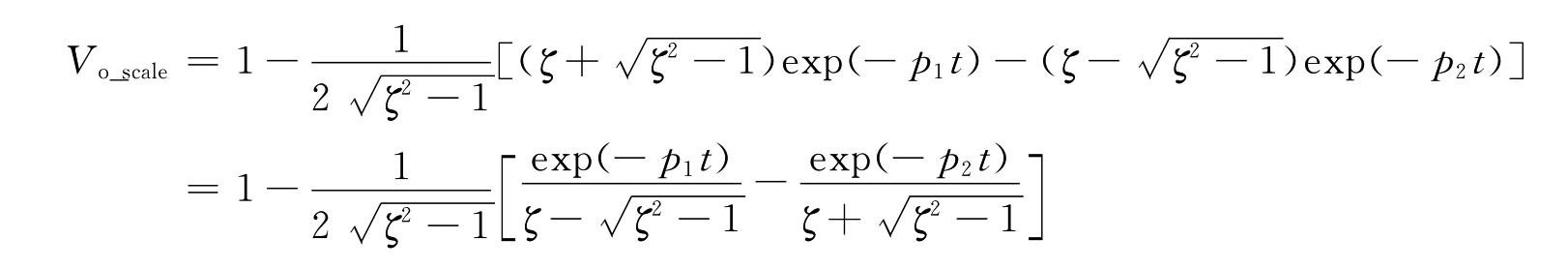
以上关系对开环和闭环均适用。在开环下，p₁为－3dB带宽，当ζ》1时，高频次极点p₂的影响越来越小并可忽略。此时的两阶系统退化为一阶系统，瞬态响应特性主要由极点p₁决定。开环瞬态响应主要决定非线性系统的小信号动态性能。在闭环下，其主极点p₁为开环GBW带宽，与次极点频率p₂相近，使次极点频率对闭环瞬态特性的影响明显增大。

现进一步考虑零点与极点形成偶对后对瞬态特性的作用。假设开环两极点系统传递函数中的次极点频率p₂＝ω_dp和零点频率z＝ω_z组成偶对，则高频下所对应的开环传递函数为

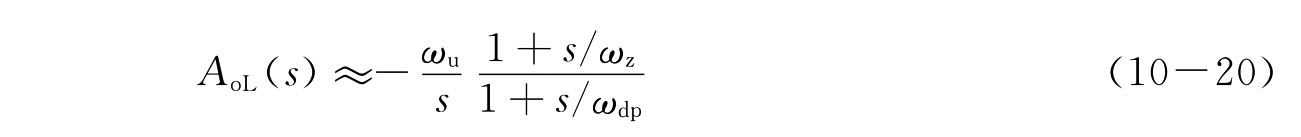
在电容反馈系数F＝C_f/C_s下形成闭环控制后，环路带宽为ω_t＝F·ω_u＝F·p₁。次极点p₂频率的高低对系统瞬态性能的影响十分显著，则相对ω_t的位置可用参量β表示，即p₂＝ω_dp＝βω_t。零点在次极点附近位置，ω_z＝ω_dp/α，其中α＝1＋ε，｜ε｜《1。闭环传递函数为

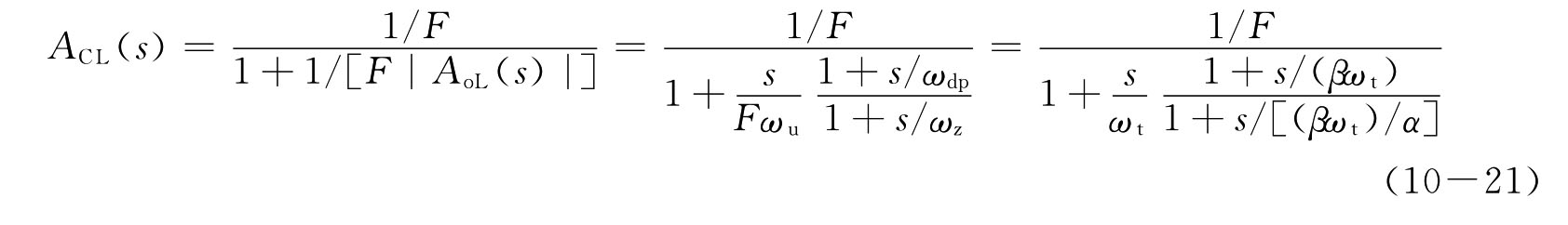
式中，α＝1＋ε为偶对中零—极点间的相互偏离程度，ε＝0则表示偶对完全重合，零—极点完全抵消。

在以上偶对的假设条件下，将各频率分量均以环路带宽ω_t为参照，则闭环传递函数可简化为

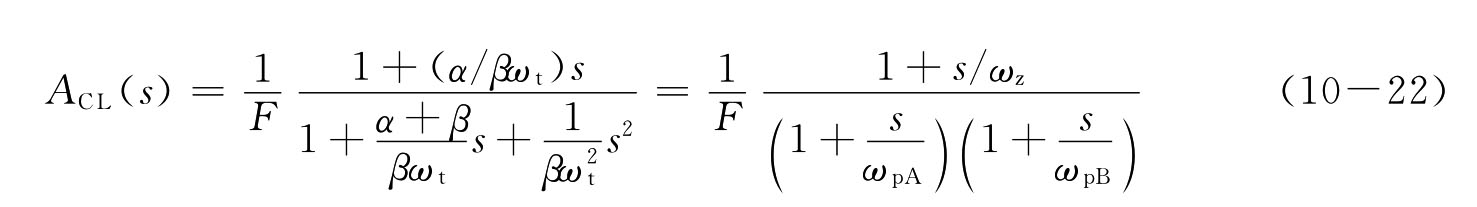
式中，ω_pA、ω_pB分别为两阶闭环系统的两个极点频率，其中一个近似为闭环带宽ω_t，另一个为闭环的次极点频率。

在形成偶对的条件下，由α→1及（β－1）₂＞0的条件，闭环系统的两个极点必定为实极点，并解得

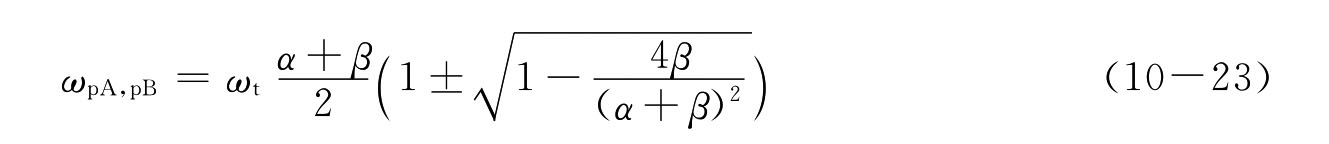
式中判别式可简化为

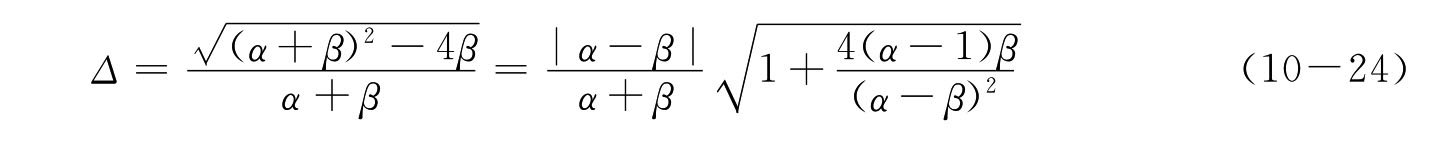
其中，在α→1的条件下近似有Δ≈｜α－β｜/（α＋β）。在α＞β的条件下代入以上关系后得到闭环的极点为

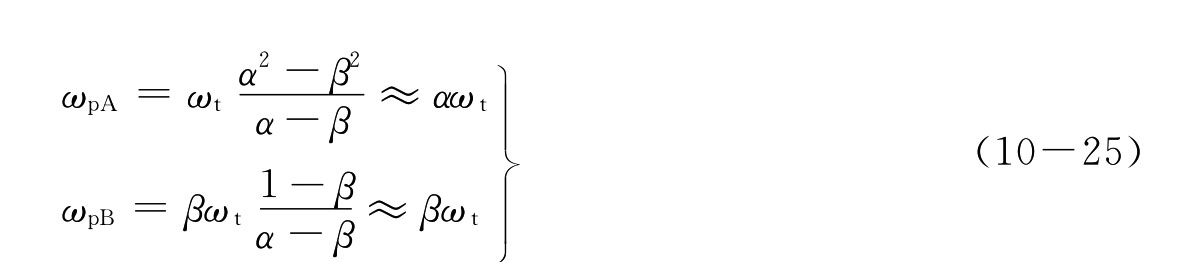
以上关系表明偶对中的极点位于闭环带宽ω_t附近。在β＞α的条件下，两者交换次序，即ω_pA＝βω_t，ω_pB＝αω_t。

以上两种状态表明，由于闭环的主极点频率为αω_t，形成偶对的极点βω_t可位于闭环带宽以内或以外，表现为β＜α或β＞α，即对应于β＜1或β＞1的变化。

对于开环系统中的偶对，传输到闭环系统中并成为闭环的偶对，偶对的相互位置关系在闭环中不仅保持不变，而且对闭环主极点位置的影响很小，仅由ω_t变化为αω_t。这里假设ω_pA＝αω_t为闭环主极点，根据各极点和零点相对ω_t频率的位置，解得的待定系数近似为

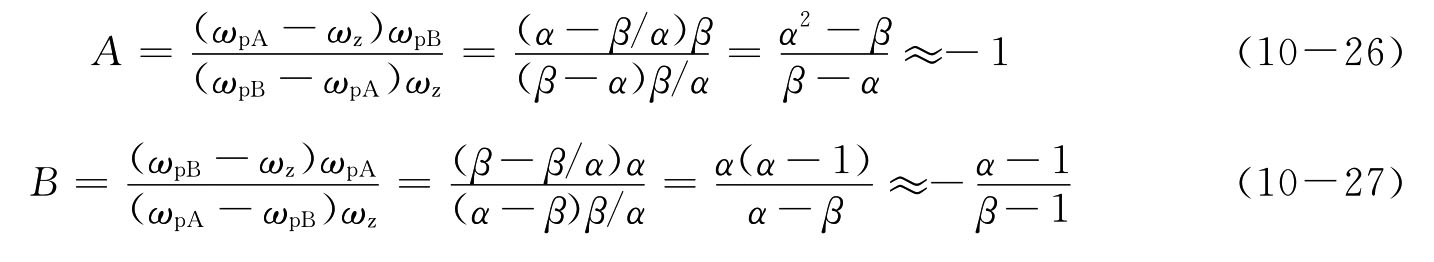
在阶跃输入激励下，包含一个零点和两个极点的闭环阶跃响应包含Aexp（－ω_pAt）＋Bexp（－ω_pBt）两个瞬态项，即

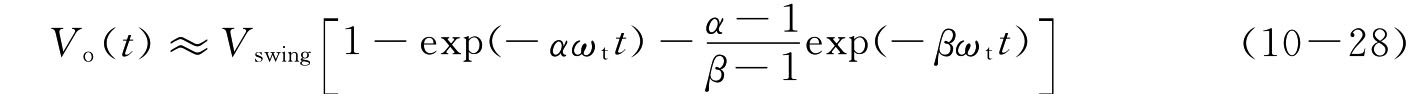
显然，当α＝1时，偶对完全消失，系统退化为单极点系统，仅由闭环主极点ω_t决定系统的瞬态响应特性。当α≠1时，偶对起作用。当β》1即偶对位于闭环带宽以外时，运放瞬态的建立时间基本不受偶对的影响；当β＜1时，建立时间中偶对的影响不可忽略，其影响程度与该项系数B有关。此时若B→0则偶对的影响可忽略；若B偏离0即α偏离1，则偶对分离度增加，对瞬态响应的影响增加。以上结果可概括为：闭环带宽外的偶对无论相互位置关系如何，其影响总能忽略；而对于闭环带宽内的偶对，只有α→1使系数B很小时，偶对的作用才能忽略，当偶对分离到一定程度时，偶对对瞬态建立时间的影响起主导作用。由于实际设计中α→1的条件很难控制，因此通常要求将偶对放置在闭环带宽即开环的单位增益带宽以外的高频位置。

2）ζ≤1或Q＞1/2条件

以上条件对应于一对共轭复极点，极点频率为p_1，2＝ω₀［ζ±j（1－ζ₂）_1/2］。在忽略零点的前提下得到待定系数为

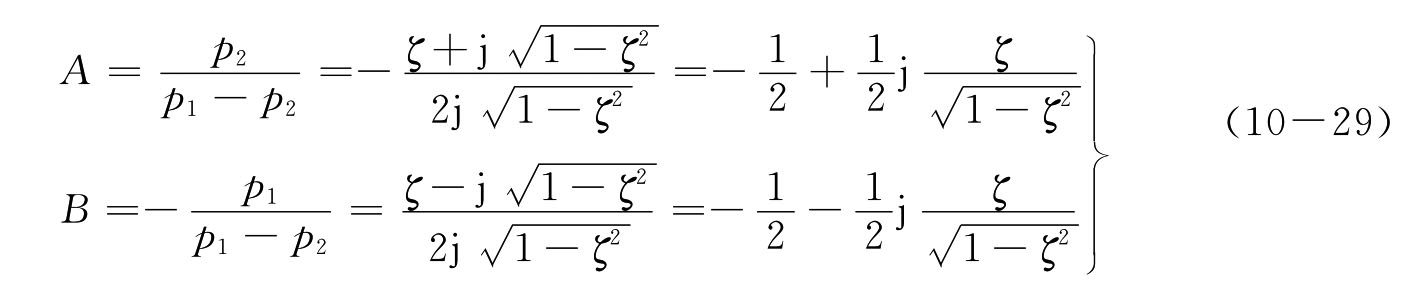
代入A、B、p₁、p₂的关系后得到的瞬态项可化简为

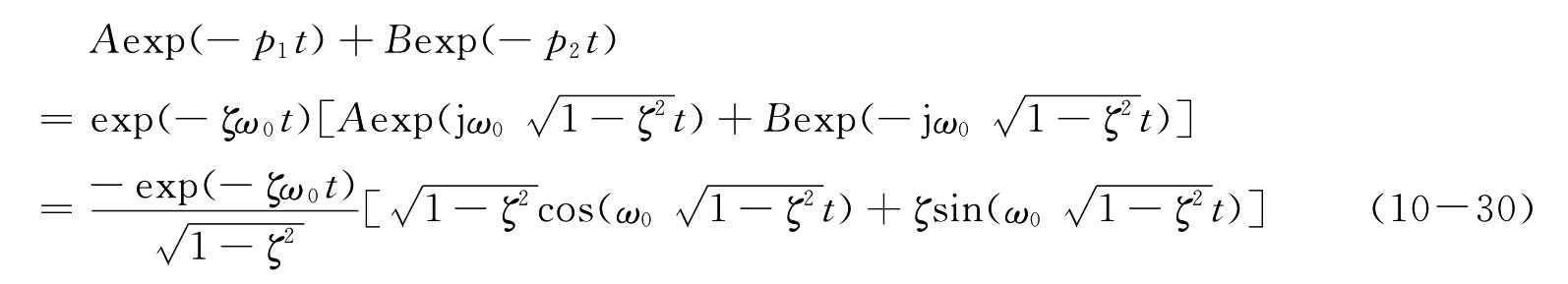
并设

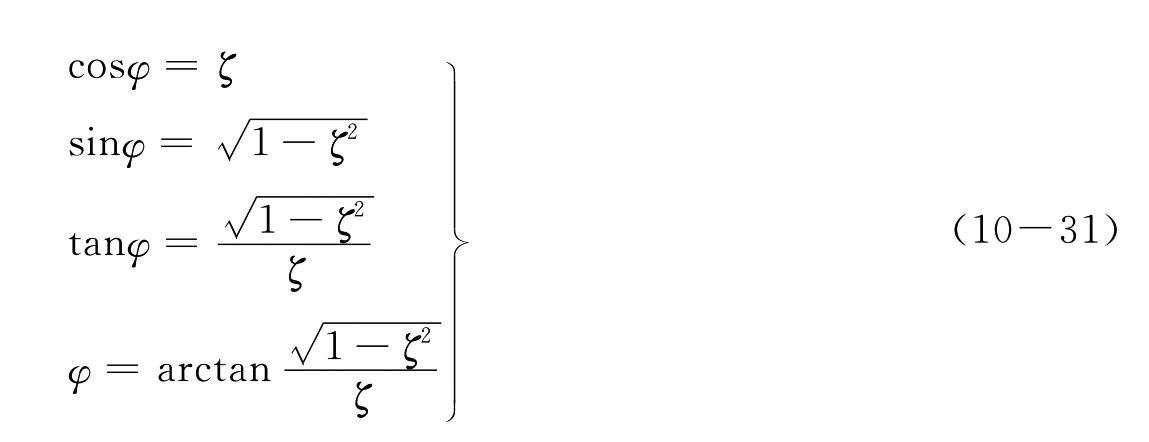
根据sin（ωt＋φ）＝sin（ωt）cosφ＋cos（ωt）sinφ的变换关系，化简后得到归一化阶跃激励下的瞬态输出响应为

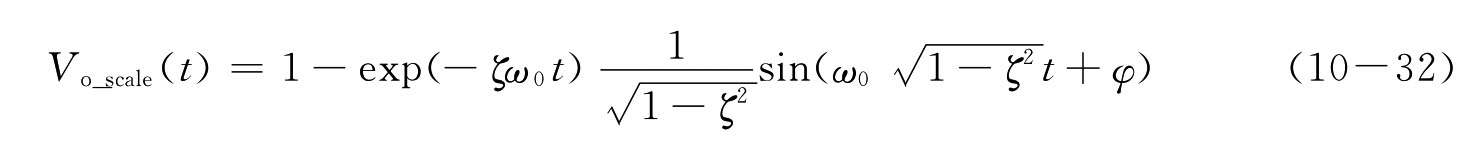
当ζ＝0时，则共轭复极点变为共轭虚极点，作为复极点的一种特例，p_1，2＝±jω₀，A＝B＝－1/2，得

V_o＿scale＝1－cos（ω₀t）　　　　　　　　　（10－33）

即输出在0和最大值之间形成等幅临界振荡。

当ζ＝1时，对应于重实极点的临界振荡，此时

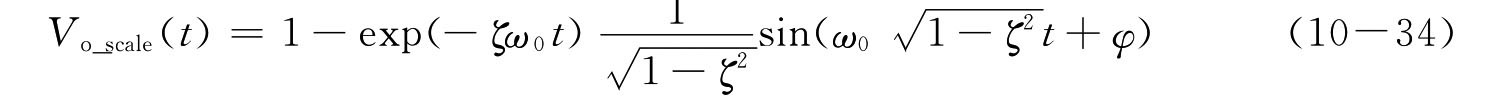
10．2．3　高阶系统小信号瞬态特性

以上两阶系统的分析方法同样可以扩展到对三阶以上高阶系统瞬态特性的分析。三极点系统可以是两级增益考虑寄生电容高频效应的结果，也可以是三级增益忽略寄生电容高频效应的正常结果。可以是开环系统，也可以是闭环系统，但在一般应用中更关心的是闭环系统。通常的设计总是使闭环主极点为开环单位增益带宽。开环的次极点与闭环次极点的关系则无定数，当开环各极点之间足够分离且次极点远高于GBW时，通常导致闭环各极点也足够分离，且对应的次极点大小不变。否则，闭环与开环的极点位置关系将发生明显的变化，其相互关系可从下式清楚看出。设p₁、p₂、p₃为开环系统A的3个极点，其中p₁为主极点，GBW为开环的单位增益带宽。当频率大于主极点频率时有

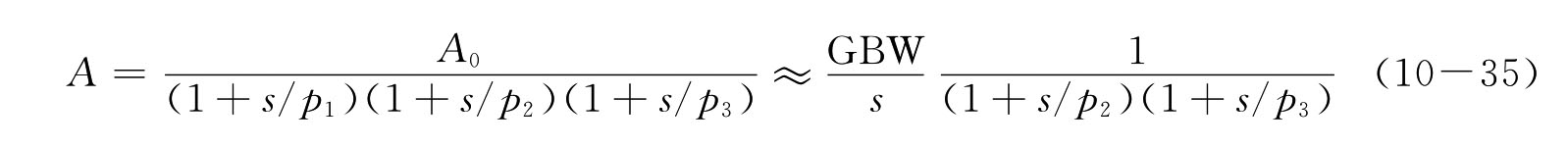
由A所构成的单位负反馈闭环系统为

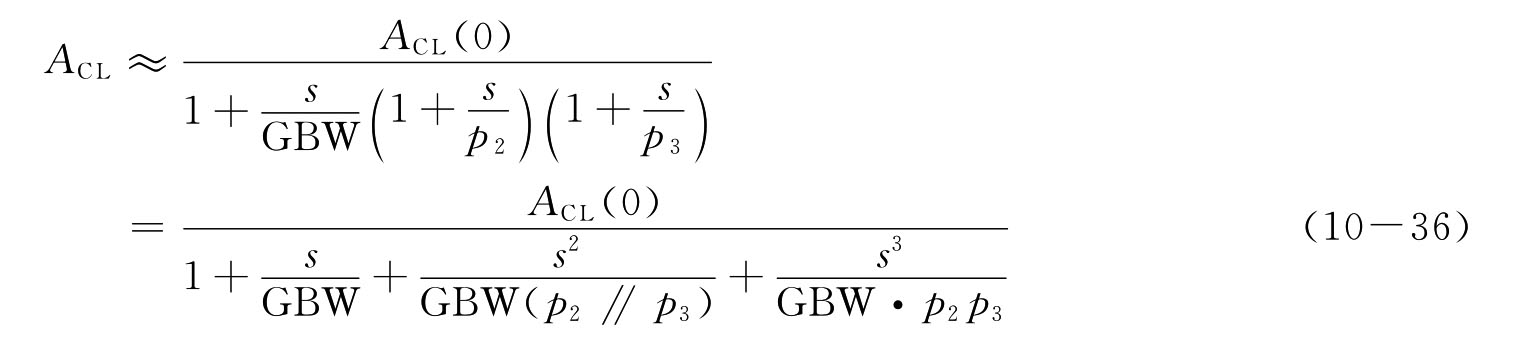
显然，当p₂》GBW、p₃》p₂时，三阶闭环系统为分离的实极点并保持GBW，p₂，p₃不变，其瞬态响应包含以上3个独立极点决定的暂态分量，系数各不相同，并由GBW决定闭环瞬态响应特性。当一个为低频主极点，另两个为一对共轭复极点时，则包含一个常系数，即与t无关系数的暂态项和一个与t有关变系数的暂态项。因此，三阶系统的瞬态响应与二阶系统并无本质的差别。

运放系统的小信号响应速度主要由低频极点决定，由此可以考察偶对对瞬态特性的影响。当偶对严格相等时，其作用完全抵消，对瞬态特性没有影响；当偶对失配时，将产生系数与失配成正比的暂态项，对瞬态特性产生影响；当偶对位于系统GBW以外时，这种影响完全可以忽略；而当偶对位于系统GBW之内时，则其影响不可忽视。偶对越小，对瞬态特性的影响越大。