双层地基承载力的分析

2.2　双层地基承载力的ANSYS分析

（1）计算参数及网格划分

本模型主要用于分析包头地区上层粉土，下层砂土的双层地基，对其极限承载力进行分析，基础宽度b＝2.0m，基础埋深1.5m，基础下上层土厚度1.5m，模型的宽度取10m，模型的高度取10m，取膨胀角φ_f＝φ，计算简图如图7所示，计算参数如表2所示，模型采用Plane42单元，计算土的自重应力。为了计算结果的精确，有效地利用电脑资源，本模型采用对称性模型，只取模型的一半来计算。单元数为1 980，节点数为2 085，有限元模型如图8所示。

图7　双层地基计算模型

图8　有限元模型

表２　各土层计算参数表

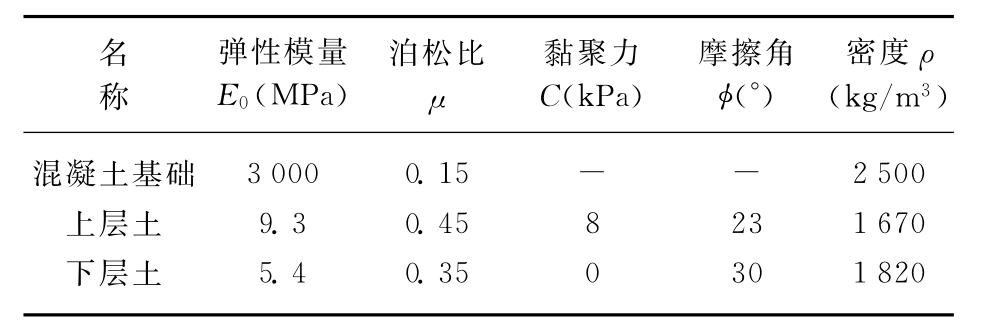
图9　开始出现塑性区

图10　塑性区向下发展

图11　塑性区到达界面

图12　塑性区开始向两边发展

图13　塑性区开始向地面发展

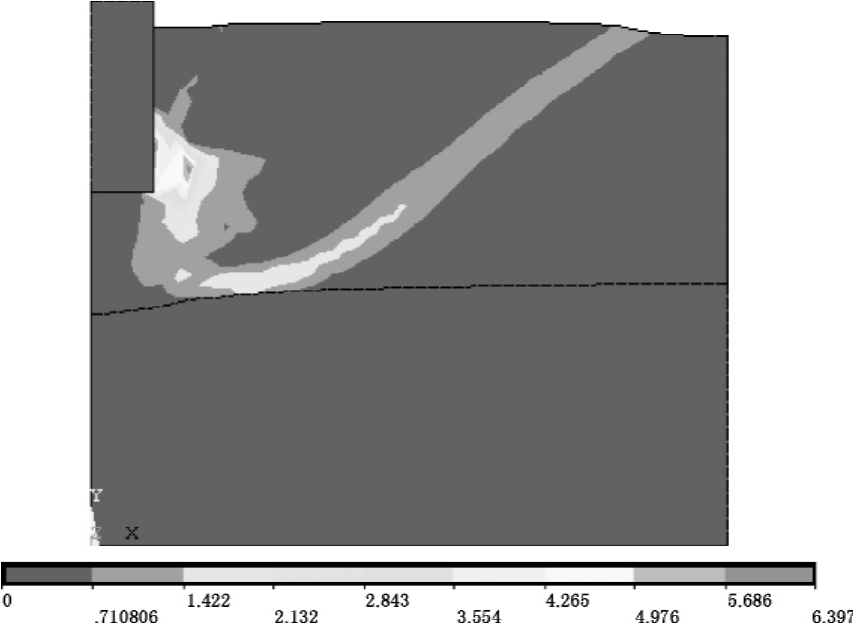
图14　形成连通的塑性区

图15　499号节点的应力应变曲线

（2）分析及结论

图9～图14展示了基础由刚开始出现塑性区一直到形成连通的塑性区（破坏）的全过程，从有限元计算的结果可以得到以下结论：地基中塑性区首先出现在基础边角处的上层土中，随着荷载的增加，塑性区向交界面处土层扩展，由于上层土相对较软，塑性区扩展较快，塑性区再往下的发展分为3种情况；

①当基础下上层土的厚度很大时，滑裂面不到达分界面，破坏形式同单层地基。

②当基础下上层土的厚度较小时，塑性区到达下层土表面，由于下层相对较硬，塑性区不穿过下层土，而是沿着分界面先向两边发展，然后向地面发展，最后形成连通区，达到破坏，地基达到极限承载力。

③当基础下上层土的厚度很小时，塑性区到达下层土表面并且穿过下层土，继续向下发展，但是向下发展的距离较小，然后开始向两边、再向地面发展，最后形成连通区，形成较复杂的滑动面以致破坏，地基达到极限承载力。

为了分析地基中某一点的应力－应变情况，所以取出基础边角的地基节点499号节点，并对其进行应力－应变分析，499号节点的应力－应变曲线如图15所示。从图中可以看出，当力较小时地基处于弹性阶段，此时应力－应变符合弹性本构关系；随着应力的逐渐增大，地基变形进入硬化阶段，此时的变形既有弹性变形也有永久变形；随着应变的增加，屈服应力也不断增加，直到破坏状态。

对模型进行极限承载力计算：ANSYS极限承载力的计算结果为952kPa；汉森加权公式极限承载力计算的结果为862kPa。