实验十二 RC一阶电路的响应及其应用
一、实验目的
1．研究一阶RC电路的零输入响应、零状态响应和全响应的变化规律和特点。
2．了解RC电路在零输入、阶跃激励和方波激励情况下响应的基本规律和特点。
3．测定一阶电路的时间常数τ，了解电路参数对时间常数的影响。
4．掌握积分电路和微分电路的基本概念。
5．学习用示波器观察和分析电路的响应。
二、实验内容
1．观测RC电路的矩形响应和RC积分电路的响应。
2．观测RC微分电路的响应。
三、实验仪器与设备
四、实验原理
1．RC电路的时域响应
从一种稳定状态到另一种稳定状态往往不能跃变，而需要一定的过程（时间），这个物理过程称为过渡过程。所谓稳定状态，是电路中的电流和电压在给定的条件下已达到某一稳定值（对交流而言是指它的幅值到达稳定），简称稳态。电路的过渡过程往往极为短暂，所以在过渡过程时的工作状态称为暂态，过渡过程又称为暂态过程。
从t＝0－到t＝0＋的瞬间，电感元件中的电流和电容元件上的电压不能跃变，称为换路定则。换路定则仅适用于换路瞬间，可根据它来确定t＝0＋时电路中电压和电流之值，即暂态过程的初始值。
在直流激励下，换路前，如果储能元件储有能量，并设电路已处于稳态，则在t＝0－电路中，电容元件可视作开路，电感元件可视作短路；如果储能元件没有储能，则在t＝0－和t＝0＋的电路中，可将电容元件视作短路，将电感元件视作开路。
含有L、C储能元件（动态元件）的电路，其响应可以由微分方程求解。凡是可用一阶微分方程描述的电路，称为一阶电路，它通常由一个储能元件和若干个电阻元件组成。对于一阶电路，可用一种简单的方法——三要素法直接求出电压及电流的响应：f（t）＝f（∞）＋［f（0＋）
其中，f（t）是电路中任一元件的电压和电流；f（∞）是稳态值；f（0＋）是初始值；τ是时间常数，对于RC电路有τ＝RC，对于RL电路有
所有储能元件初始值为零的电路对激励的响应称为零状态响应。电路在无激励情况下，由储能元件的初始状态引起的响应称为零输入响应。电路在输入激励和初始状态共同作用下引起的响应称为全响应，它是零输入响应和零状态响应之和，体现了线性电路的可加性。全响应也可看成是稳态响应和暂态响应之和，暂态响应的初始值与初态和输入有关，而其随时间变化的规律仅决定于电路的R、C参数；稳态响应仅与输入有关。当t→∞时，暂态过程趋于零，过渡过程结束，电路进入稳态。
图4－46 一阶RC电路
2．RC电路的时间常数τ
如图4－46所示电路为一阶RC电路。RC电路充放电的时间常数τ可以从示波器观察的响应波形中估算出来。设时间坐标单位t确定，对于充电曲线来说，幅值上升到终值的63．2%所需的时间即为一个τ（见图4－47（a））；对于放电曲线来说，幅值下降到初值的36．8%所需的时间即为一个τ（见图4－47（b））。时间常数τ越大，衰减越慢。
图4－47 RC电路充放电曲线
3．微分电路
微分电路和积分电路是RC一阶电路中比较典型的电路，对电路元件参数和输入信号的周期有着特定的要求。微分电路必须满足两个条件：一是输出电压必须从电阻两端取出，二是由于R值很小，因而τ＝RC《tp，其中tp为输入矩形方波ui的1／2周期。如图4－48所示，因为此时电路的输出信号电压近似与输入信号电压的导数成正比，故称为微分电路。
只有当时间常数远小于脉宽时，才能使输出很迅速地反映出输入的跃变部分。而当输入跃变进入恒定区域时，输出也近似为零，形成一个尖峰脉冲波，故微分电路可以将矩形波转变成尖脉冲波，且脉冲宽度越窄，输入与输出越接近微分关系。
4．积分电路
积分电路必须满足两个条件：一是输出电压必须从电容两端取出，二是τ＝RC》tp。如图4－49所示，因为此时电路的输出信号电压近似与输入信号电压对时间的积分成正比，故称为积分电路。
由于τ＝RC》tp，因此充放电很缓慢，UC增长和衰减很缓慢。充电时Uo＝UC《UR，因此Ui＝UR＋Uo≈UR。积分电路能把矩形波转换为三角波、锯齿波。为了得到线性度好且具有一定幅度的三角波，需要掌握时间常数τ与输入脉冲宽度的关系。方波的脉宽越小电路的时间常数τ越大，充放电越缓慢，所得三角波的线性越好，但幅度亦随之下降。
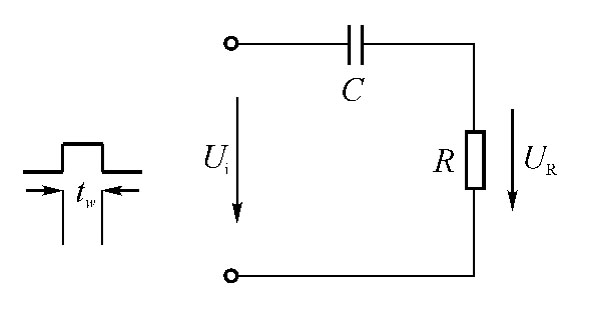
图4－48 RC微分电路
图4－49 RC积分电路
五、实验注意事项
1．调节电路分析实验装置各旋钮时，动作不要过猛。实验前，需熟读双踪示波器的使用说明，特别是观测双踪时，要特别注意开关、旋钮的操作与调节。
2．信号源的接地端与示波器的接地端要连在一起，以防外界干扰影响测量的准确性。
3．示波器的辉度不应过亮，尤其是光点长期停留在荧光屏上不动时，应将辉度调暗，以延长示波器的使用寿命。
4．熟读仪器的使用说明，做好实验预习，准备好画图用的图纸。
六、实验内容与步骤
实验线路板的结构如图4－50所示，认清R、C元件的布局及其标称值，各开关的通断位置等。
图4－50 一阶、二阶动态电路实验线路板
1．观测RC电路的矩形响应和RC积分电路的响应
（1）选择动态电路板上的R、C元件，使R＝30kΩ、C＝1 000pF（0．001μF）组成如图4－46所示的RC充放电电路，E为函数信号发生器输出。取Umax＝3V、f＝1kHz的方波电压信号，并通过两根同轴电缆，将激励源Ui和响应UC的信号分别连至示波器的两个输入口YA和YB，这时可在示波器的屏幕上观察到激励与响应的变化规律。
（2）令R＝30kΩ、C＝0．01μF，观察、描绘响应的波形，并根据电路参数求出时间常数。少量地改变电容值或电阻值，定性地观察其对响应的影响，记录观察到的现象。
（3）增大R、C的值，使之满足积分电路的条件τ＝RC》tp，观察其对响应的影响。
2．观测RC微分电路的响应
（1）选择动态电路板上的R、C元件，组成如图4－48所示的微分电路。令C＝0．01μF、R＝1kΩ，在同样的方波激励（Um＝3V、f＝1kHz）作用下，观测并描绘激励与响应的波形。
（2）少量地增减R值，定性地观测对响应的影响，并作记录，描绘响应的波形。
（3）令C＝0．01μF、R＝100kΩ（元件箱），计算τ值。在同样的方波激励（Umax＝3V，f＝1 kHz）作用下，观测并描绘激励与响应的波形。分析并观察当R增至1MΩ时，输入、输出波形较之前有何本质上的区别。
七、实验报告要求
1．根据实验观测的结果，在方格纸上绘出RC一阶电路充放电时UC的变化曲线将曲线测得值与计算得到的参数值作比较，分析误差原因。
2．根据实验观测结果，归纳总结积分电路和微分电路的形成条件，阐明波形变换的特征。
八、实验思考题
1．什么样的电信号可作为RC一阶电路零输入响应、零状态响应和完全响应的激励信号？
2．已知RC一阶电路中R＝30kΩ，C＝0．01μF，试计算时间常数τ，并根据τ值的物理意义，拟订测量τ的方案。
3．何谓积分电路和微分电路？它们必须具备什么条件？它们在方波脉冲信号的激励下，输出信号的波形的变化规律如何？这两种电路有何功用？
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
