单变量的统计分析

单变量的统计分析_社会调查与统计

第一节　单变量的统计分析

对统计量的简单处理和描述是数据分析的基本功能，也是进行复杂分析的基础。SPSS软件提供的基本统计量可以分为三类:描述样本分布情况的统计量，描述集中趋势的统计量及描述离散程度的统计量。通过计算样本的频数、百分比、均值、标准差等统计量，辅助于SPSS软件提供的图形，把数据的基本特征和整体分布情况呈现出来。基本统计量的统计分析主要集中在Analyze下的Descriptive Statistics分析模块中(见图10-2)。

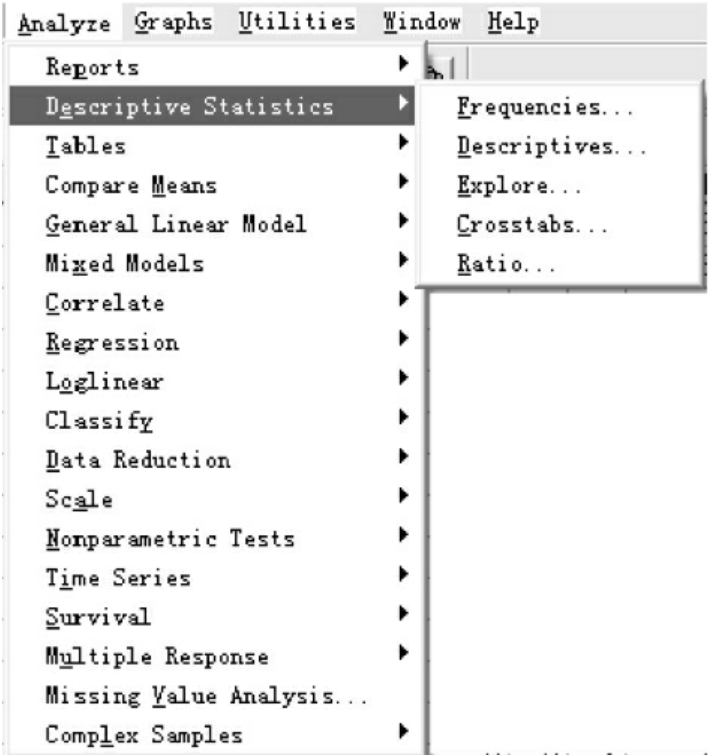
图10-2　Analyze对话框

Descriptive Statistics包括的基本统计功能有以下几个方面，其中有些功能大致相同。

(1)Frequencies:频数分析。

(2)Descriptives:描述统计量分析。

(3)Explore:探索分析。

(4)Crosstabs:交叉表(交互分类表)分析。

(5)Ratio:比率分析。

一、频数分析(Frequencies)

频数分析是统计分析中最常用的功能之一，用以描述变量的分布特征，主要适用于离散型数据，即定类变量和定序变量的测量，定距以上层次的变量因取值较多，会使得频数分析表较为庞大，可现对其取值进行分组，再进行频数分析。频数分析结果通过频数分布表呈现出来。

1.频数分析的过程

频数分析的基本过程如下:

(1)打开数据文件，点击Analyze→Descriptive Statistics→Frequencies，打开如图10-3的对话框。左侧源变量窗口列出的是该文件的全部变量。

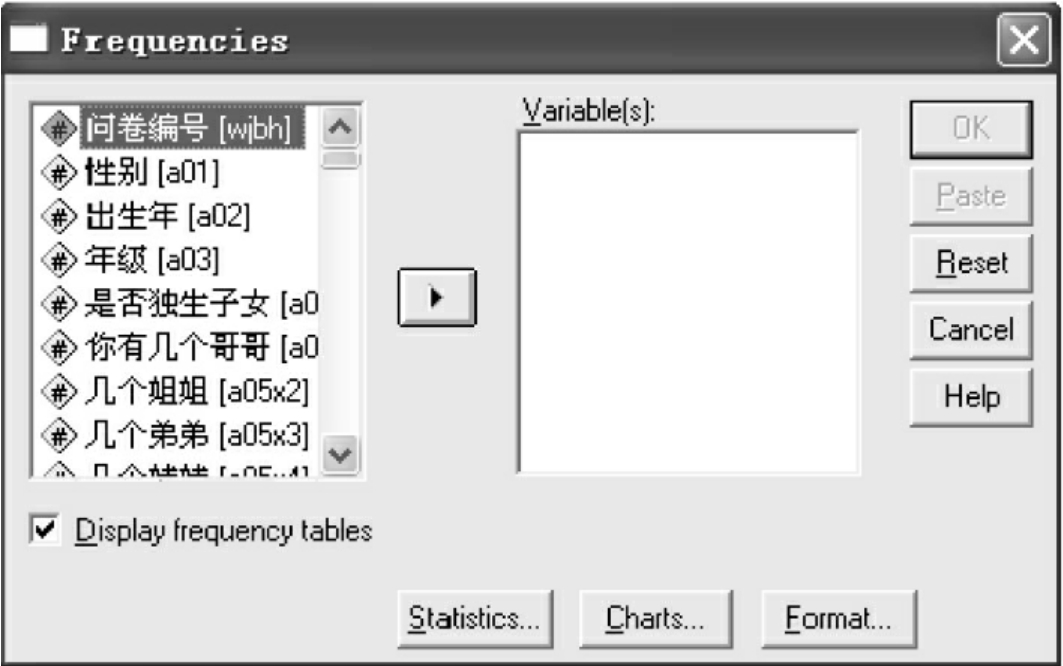
图10-3　Frequencies对话框

Display frequency tables:是否在结果中输出频数表的选项。系统默认是输出频数表。

OK是运行，Paste是在命令窗口粘贴执行的命令，Reset是重新设置，Cancel是取消统计分析，Help是提供帮助。

(2)Variable(s):确定进行频数分析的变量。

从左侧的源变量窗口中选择将要进行频数分析的变量，放入Variable(s)窗口。

(3)Statistics:选择统计分析结果。单击Statistics按钮，打开如图10-4的对话框。

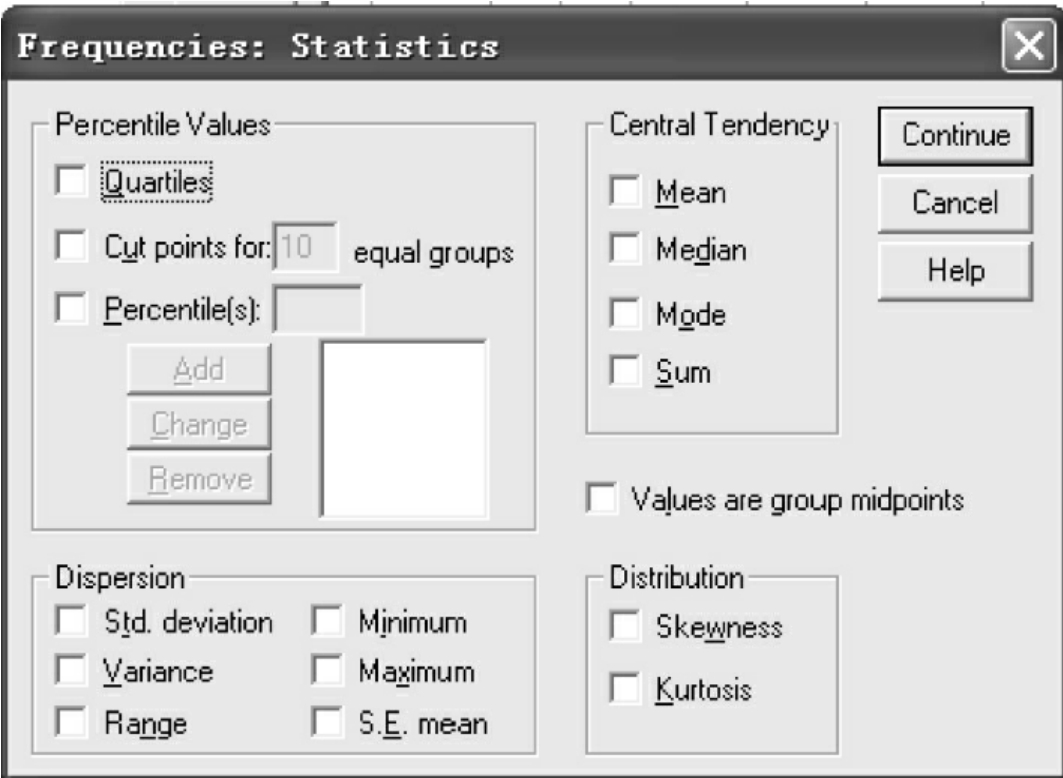
图10-4　统计量选择对话框

该对话框中包括四个选项栏。每个选项栏中包括若干个可选项。可选项被选中后，将在输出结果窗口输出对应的统计结果。

①Percentile Values:百分位数选项栏。

●Quartiles:四分位数，包括上四分位和下四分位；

●Cut points for equal groups:每隔指定的百分位间距输出一个百分位数；

●Percentile(s):指定输出的百分位数，如指定输出位于5%和95%的变量的取值。

②Central Tendency:集中趋势测量选项栏。

●Mean:平均数；

●Median:中位数；

●Mode:众数；

●Sum:总和。

③Dispersion:离散趋势测量选项栏。

●Std.deviation:标准差；

●Variance:方差；

●Range:全距；

●Minimum:最小值；

●Maximum:最大值；

●S.E.mean:标准误。

④Distribution:分布特征选项栏。

●Skewness:偏度系数；

●Kurtosis:峰度系数。

系统默认状态是不输出任何选项，只输出统计变量的频数分布表，可根据需要在上面的对话框中选择。选择完之后，单击Continue按钮，返回频数分析主对话框。

(4)Charts:选择输出图形。单击“Charts”按钮，打开绘图对话框，见图10-5。

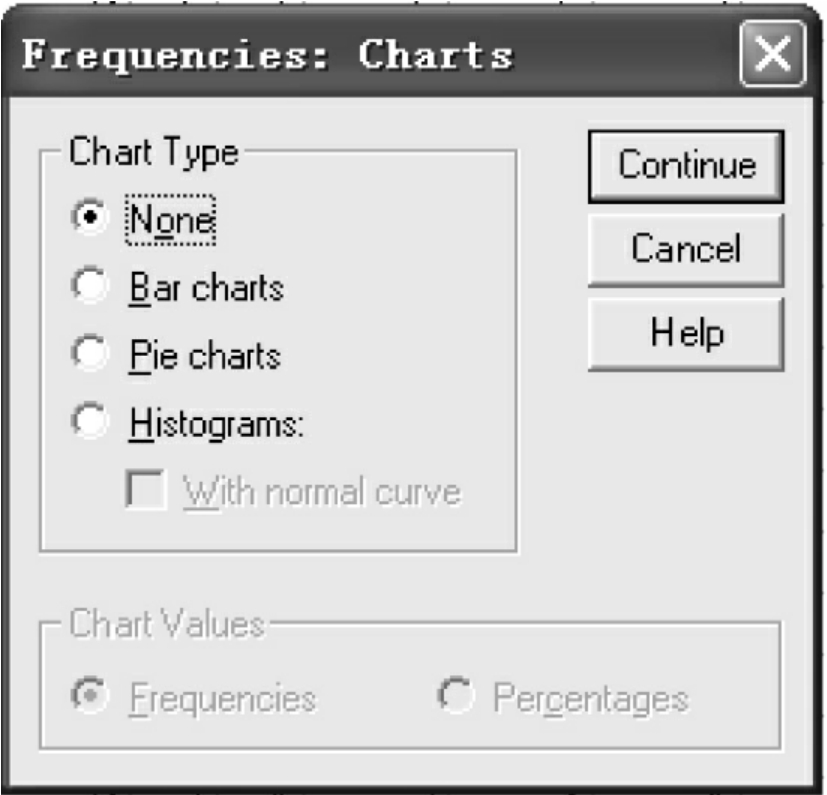
图10-5　选择输出图形对话框

该对话框中的两个选项栏分别是:

①Chart Type:统计图类型选项栏。

●None:不生成图。这是系统默认选项；

●Bar chart:绘制条形图；

●Pie chart:绘制饼形图。

②Histogram:绘制直方图。对于直方图还可以选择是否加上正态曲线(With normal curve)。选择了Histogram选项，可激活With normal curve选项。

③Chart Values:作图数据的选项栏。选择了Bar chart或Pie chart，便激活了Chart Values选项栏。

●Frequencies:按频数作图；

●Percentages:按百分比作图。

单击Continue按钮返回频数分析主对话框。

(5)Format:确定输出格式。单击Format按钮打开格式对话框，见图10-6。通过该对话框可以对输出频数表的格式进行选择。

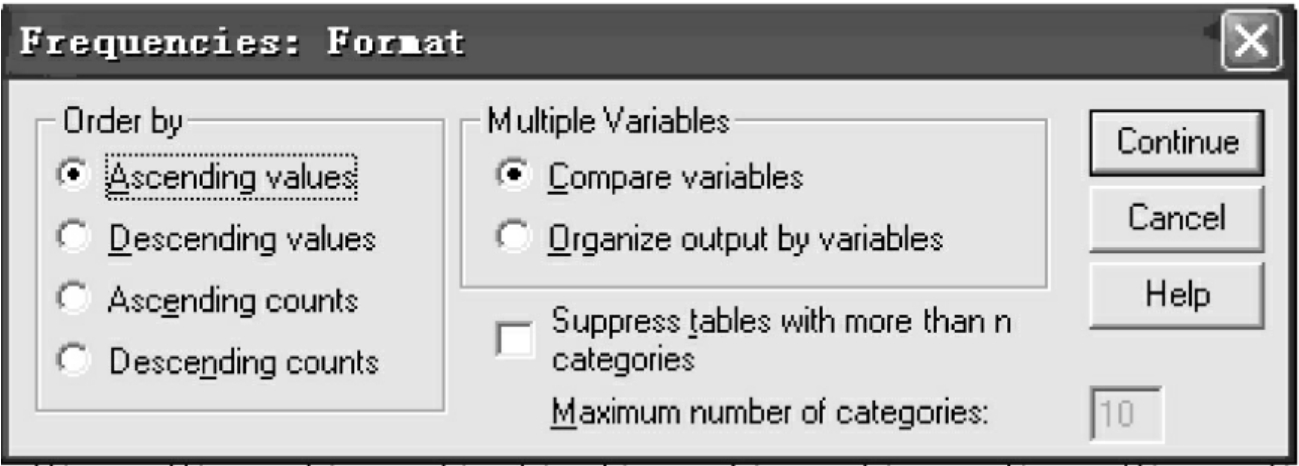
图10-6　格式对话框

①Order by:定义频数表的排列次序。

●Ascending values:按变量值的升序从小到大排列。这是系统默认选项；

●Descending values:按变量值的降序从大到小排列；

●Ascending counts:按频数的升序从小到大排列；

●Descending counts:按频数的降序从大到小排列。

②Multiple Variables:多变量选项栏。该栏中的选项适用于两个以上变量作频数表。

●Compare variables:比较变量，如果选择了两个以上变量作频数表，则选择此项，可以将它们的结果在同一个频数表中输出；

●Organize output by variables:按各变量单独输出。结果会在不同的表中显示；

●Suppress tables with more than n categories:表格分成n栏。激活than后面的窗口。输入的数字n是频数表分组数的最大设定。当频数表的分组数大于设定的n值时，禁止它在结果中输出，以避免产生巨型表格。单击Continue按钮返回频数分析主对话框。

(6)单击OK按钮，提交运行。在输出结果窗口中看到输出的频数分布表。

2.实例分析

例1　对data10.1.1中“文化程度”进行频数分析，并输出直方图。

打开数据，执行以下操作:

(1)点击Analyze→Descriptive Statistics→Frequencies，打开Frequencies对话框。

(2)把“文化程度”变量放入Variance(s)窗口。

(3)单击Statistics按钮，选择Mode，然后单击Continue。

(4)单击Charts按钮，选择Histograms，点With normal curve，然后单击Continue。

(5)单击OK按钮，提交运行。在输出结果窗口看到表10-1、表10-2和图10-7的结果。

表10-1　统计概要

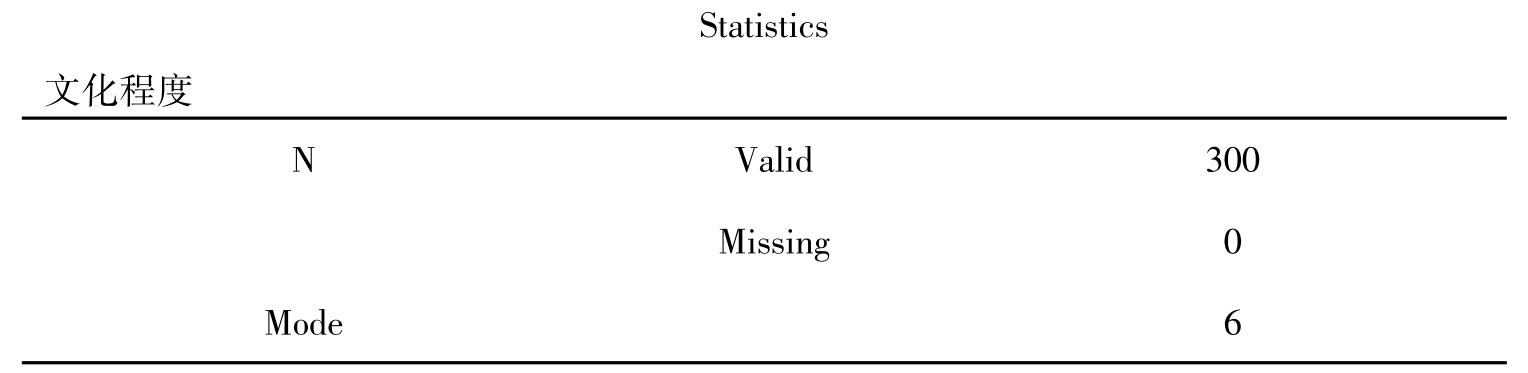
上表是统计概要，说明分析的有效样本数是300，缺失值是0，众数是6，即本科毕业。

表10-2　频数分布表

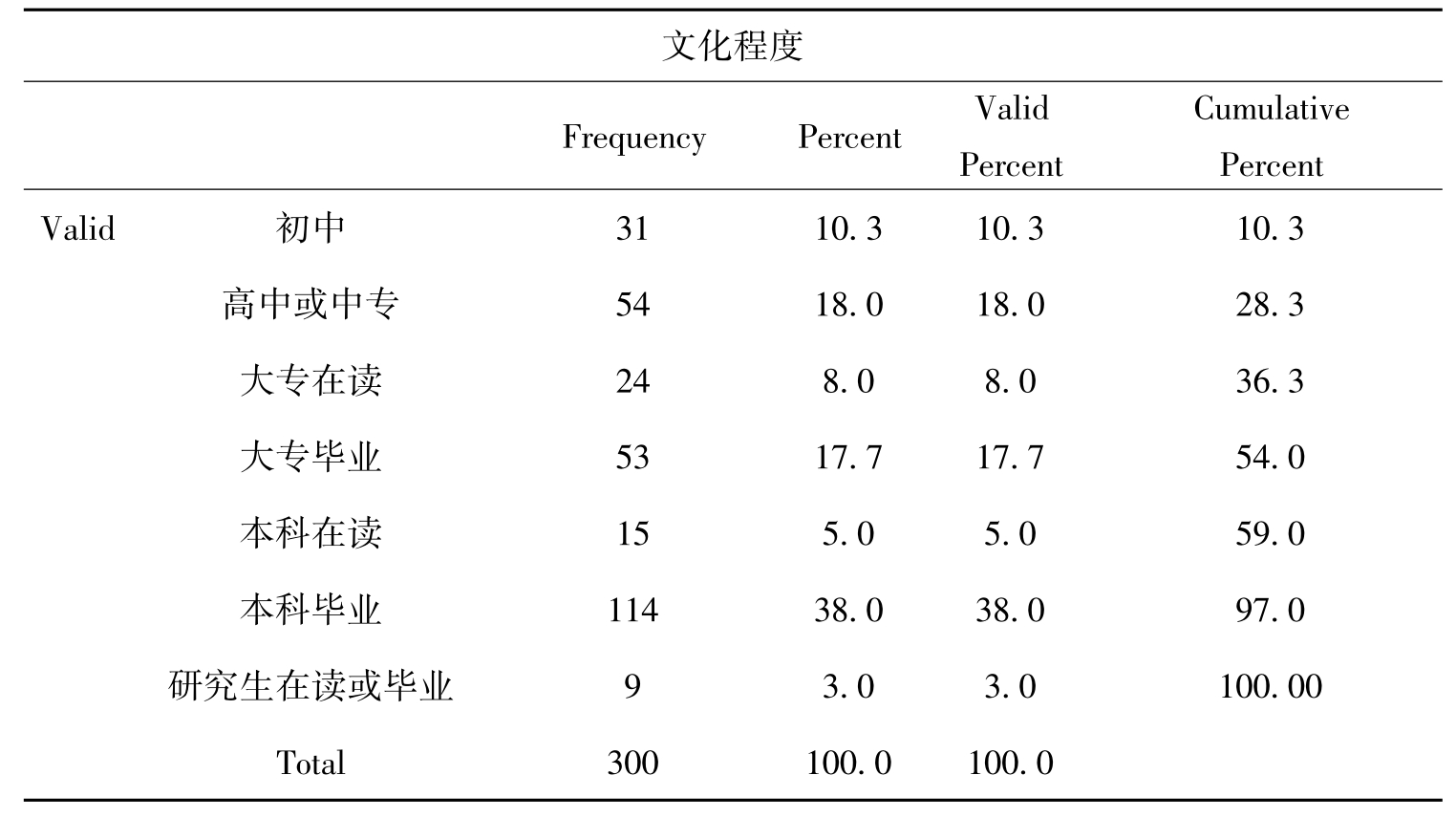
表10-2是频数分布表，是社会统计分析中最常用的样本资料的呈现形式。频数分布表通过对原始资料的初步简化，可以简洁明了地反映原始数据的情况。统计分析表的形式多种多样，但统计表的基本要求是一样的，一般由四个主要部分组成:表头、行标题、列标题和数字资料。另外，根据需要还可在统计表下方注明附加信息。其中，Frequency是频数，Percent是百分比，Valid Percent是有效百分比，Cumulative Percent是累积百分比。结果输出了各文化程度的人数，所占的百分比，有效百分比和累计百分比。

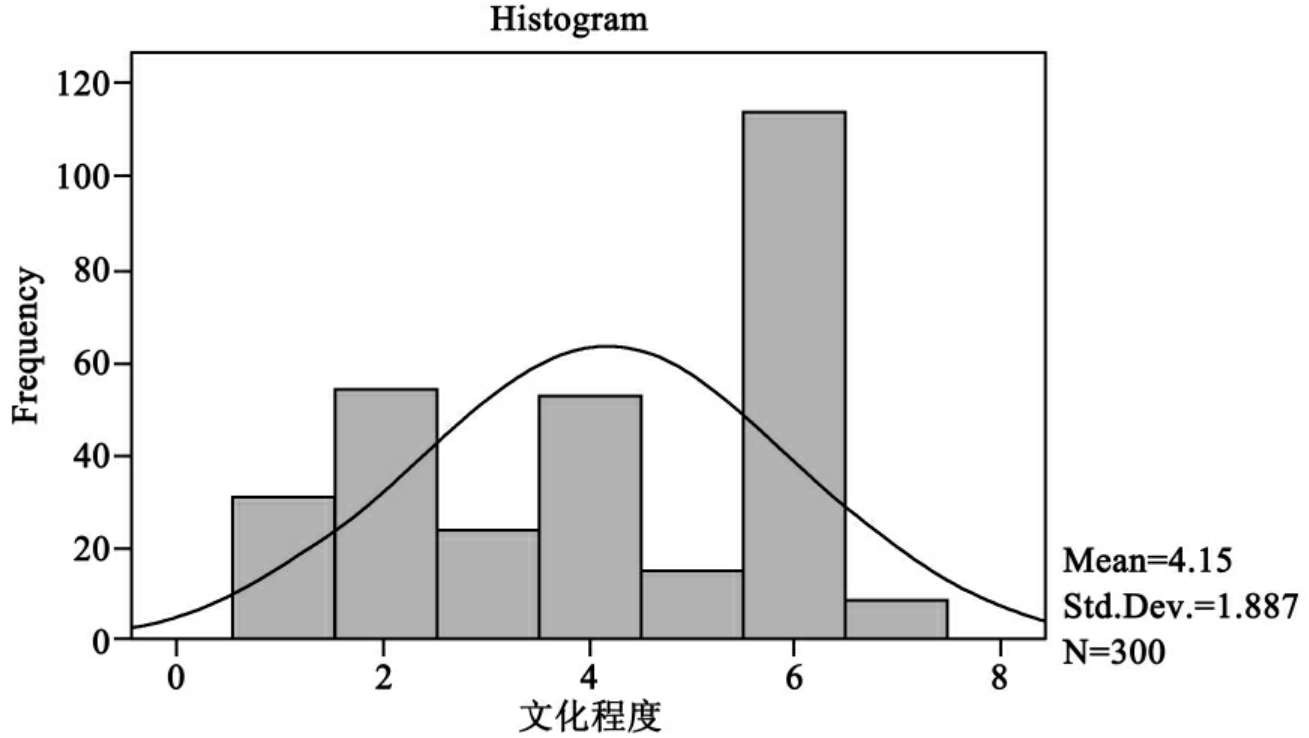
图10-7　文化程度的频数直方图

例2　对data10.1.1中“月收入”进行频数分析。

打开数据，执行以下操作:

(1)点击Analyze→Descriptive Statistics→Frequencies，打开Frequencies对话框。

(2)把“月收入”变量放入Variance(s)窗口。

(3)单击Statistics按钮，选择Mean，Median，Std.deviation，Variance，然后单击Continue按钮。

(4)单击OK按钮，提交运行。在输出结果窗口看到统计概要和频数分布表。下面仅就与上述结果不同之处进行说明(见表10-3)。

表10-3　统计概要

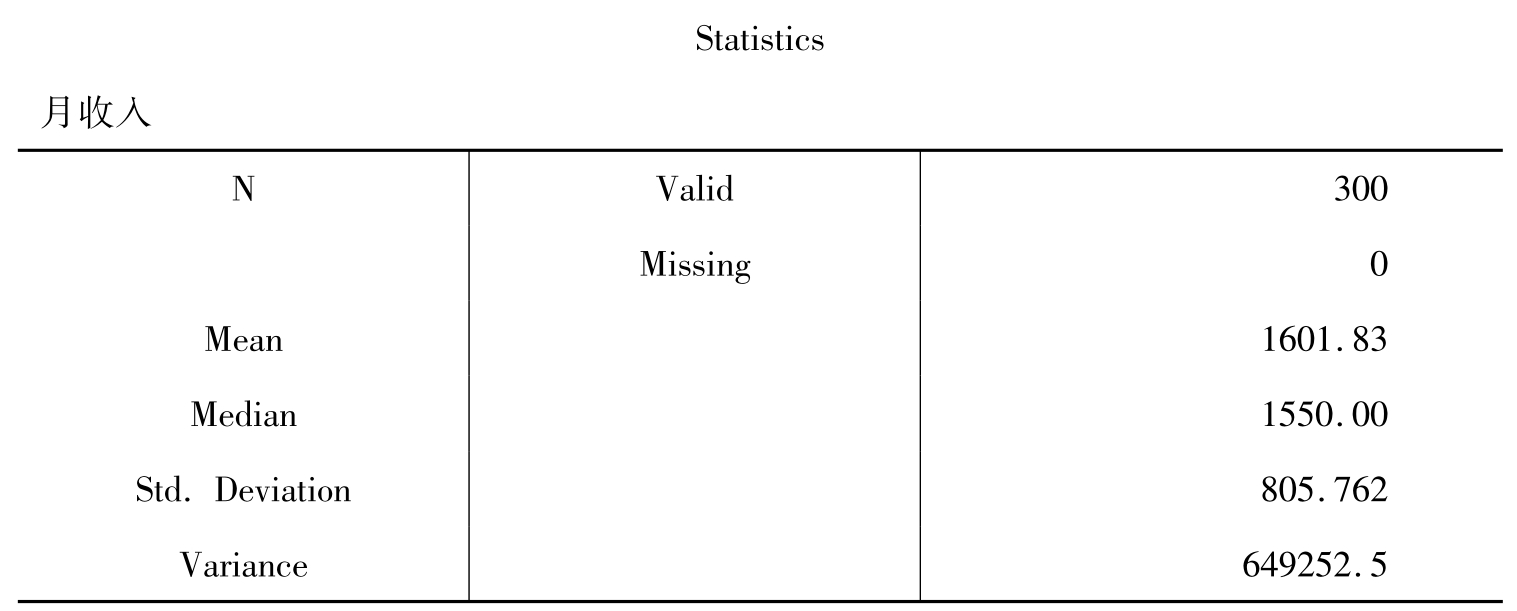
表10-3的统计概要分别说明的是统计样本的有效个案数是300，缺失值是0，均值是1601.83，中位数是1550.00，标准差是805.762，方差是649252.5。

二、描述统计(Descriptives)

Descriptives也是对变量的基本描述统计命令，主要针对的是定距以上变量的测量。

1.Descriptives的分析过程

打开数据库，执行以下操作；

(1)点击Analyze→Descriptive Statistics→Descriptives，打开对话框，见图10-8。Save standardized values as variables是将原始数据的标准值存为新变量的选项。选择该项后，系统将以原始数据的标准值生成一个新变量。系统默认不选择此项。

(2)选择要分析的变量。从源变量框中选择要分析的变量放入Variable(s)窗口。

(3)Options:选择描述统计量。单击Options按钮，打开如图10-9的对话框。

该对话框中的大部分内容与Frequencies中Statistics选项中的统计量一样。在这个对话框中，系统默认状态是输出平均值、标准差、最大值和最小值。其他选项可根据需要进行选择。

Display order是确定统计结果排列顺序的选项栏。当用户选择了多个变量进行统计时，在输出结果中如何排列这些统计结果，由该栏中的选项决定。

①Variable list:输出的统计结果按变量顺序列表。这是系统默认的选项；

②Alphabetic:输出的统计结果按字母顺序列表；

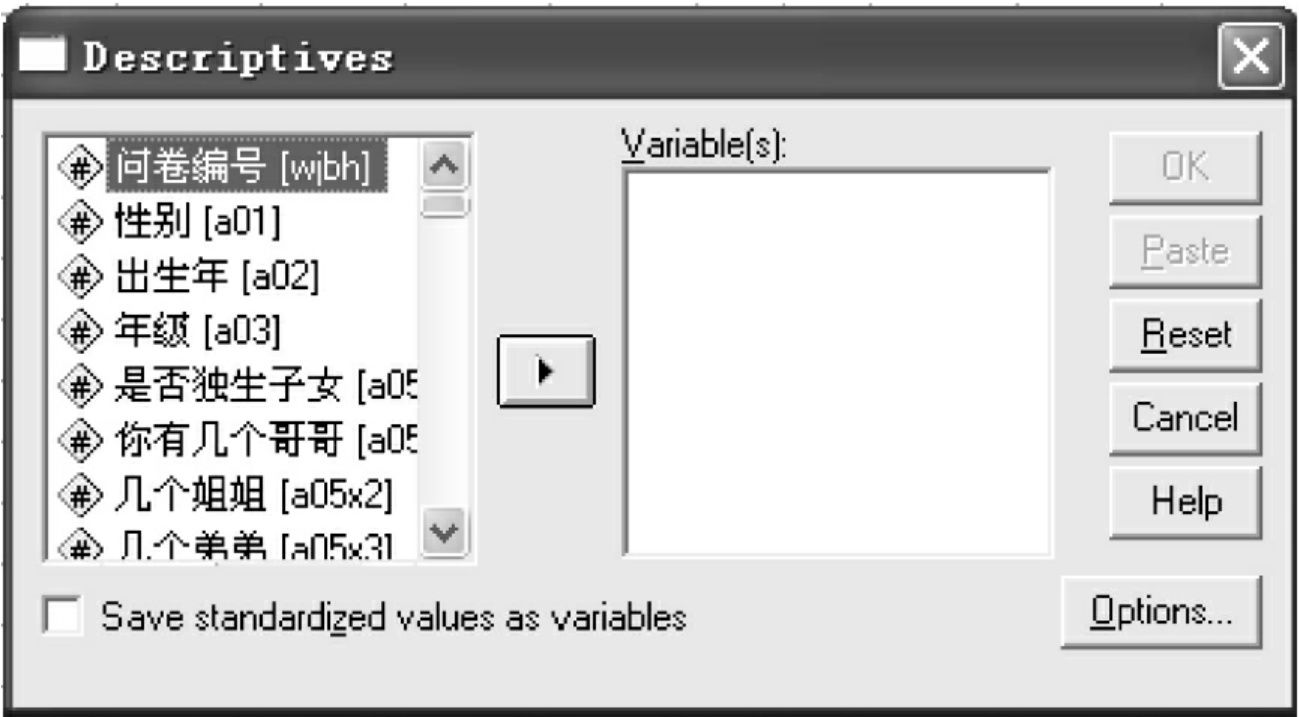
图10-8　Descriptives对话框

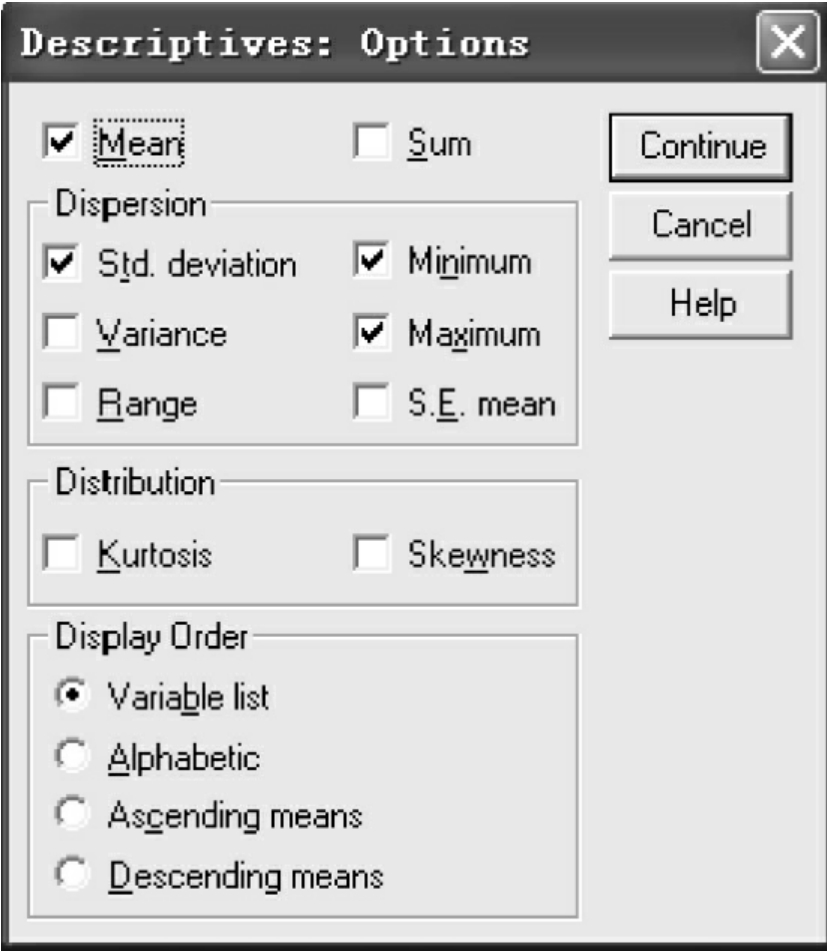
图10-9　Options对话框

③Ascending means:输出的统计结果按照平均值的升序排列；

④Descending means:输出的统计结果按照平均值的降序排列。

上述选项都确定以后，单击Continue按钮返回Descriptives主对话框。

(4)单击OK按钮，提交运行。在输出结果窗口看到统计结果。

2.实例分析

例3　对数据data10.1.2中“教育年数”、“现在工资”和“初始工资”进行描述统计。

打开数据，执行以下操作:

(1)点击Analyze→Descriptive Statistics→Descriptives，打开对话框。

(2)选择“教育年数”、“现在工资”、“初始工资”进入Variable(s)窗口。

(3)单击Options按钮，选择Variance，其他选项默认。单击Continue按钮。

(4)单击OK按钮，提交运行。在结果窗口输出表10-4的结果。

表10-4　描述统计结果

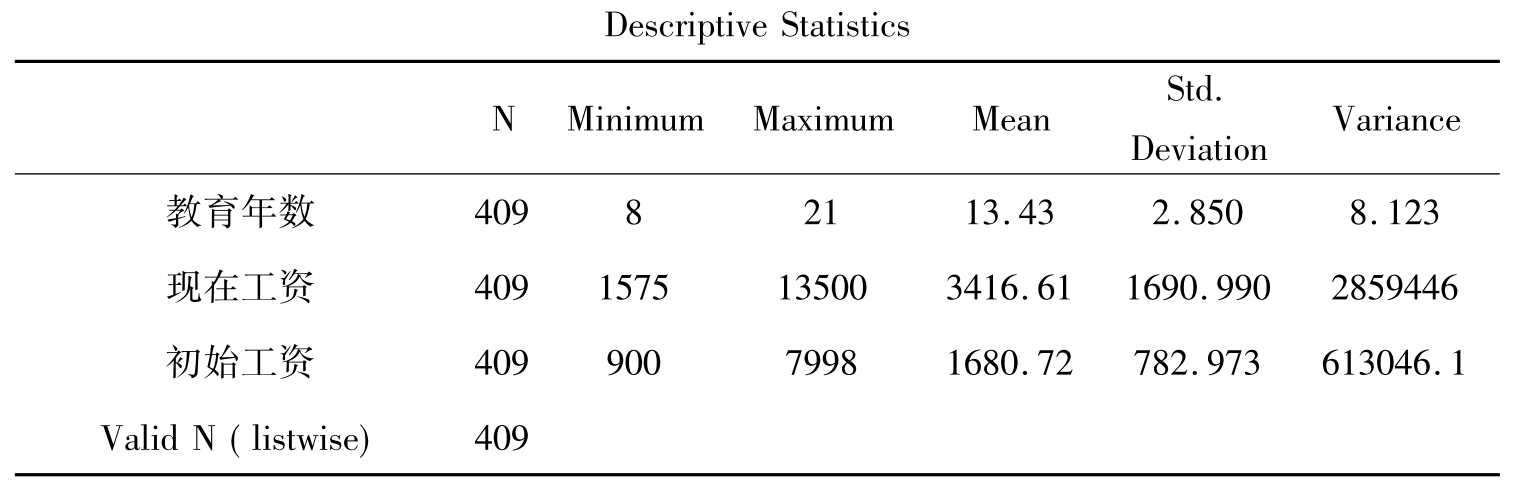
表10-4的结果中，变量是按照选择变量的顺序排列的。三个变量的有效数都是409，没有缺失值。分析结果中清楚的列出了教育年数、现在工资和初始工资的最小值、最大值、均值、标准差和方差。以现在工资为例，可以看出，调查的409人中，现在工资的最小值是1575，最大值是13500，平均值是3416.61，标准差是1690.99，方差是2859446。

三、探索分析(Explore)

探索分析也是描述单变量基本情况的统计方法，它的很多统计量与Frequencies和Descriptives是一样的，不同的是Explore增加了变量分组的功能。Explore可以分析变量在分组或不分组情况下统计量与图形，并进行假设检验。其中的图形可以直观地将奇异值、非正常值、丢失的数据以及数据本身的特点呈现出来。由于许多统计过程都要求数据服从正态分布，因此在对数据判断之前除了检查错误的数据、极端值、奇异值等，还需要检查数据的分布是否符合正态分布的要求。检查数据正态性的最直观的方法就是图示法，必要时需要借助统计量进行判断。需要说明的是，几乎所有的正态分布检验都有理由认定数据拒绝正态分布，但是如果数据足够大，则不必勉强观测量一定服从正态分布，只要接近正态分布即可。

1.Explore的分析过程

打开数据库，执行以下操作:

(1)点击Analyze→Descriptive Statistics→Explore，打开如图10-10及图10-11的对话框。

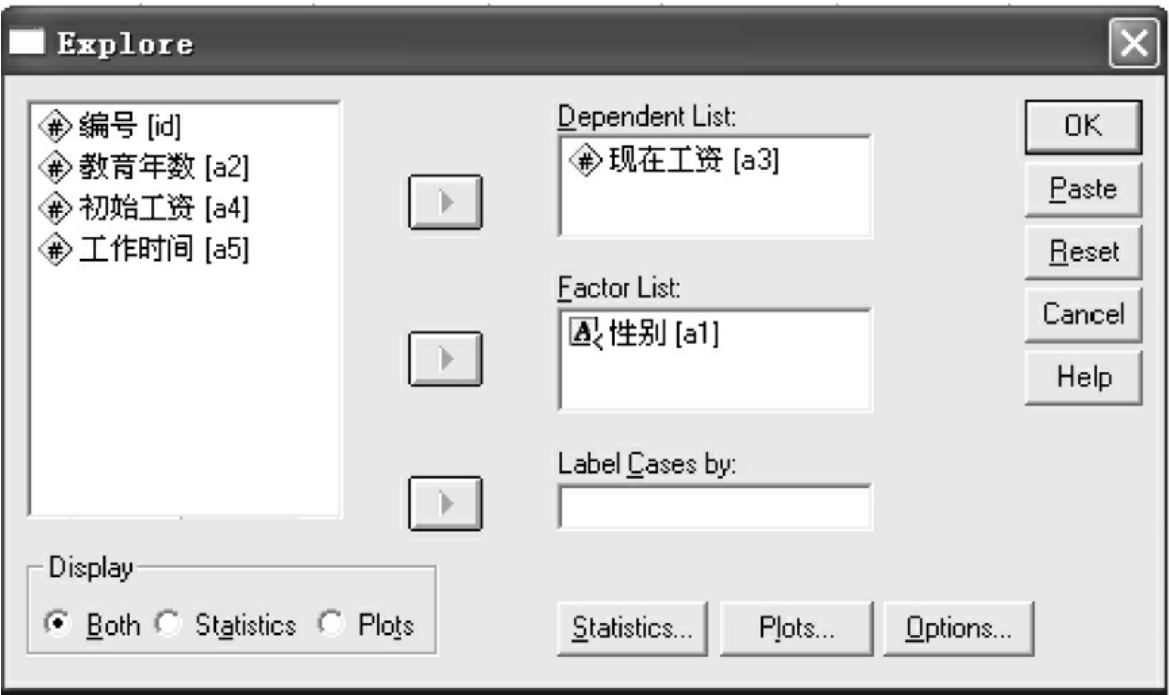
图10-10　Explore对话框

(2)选择要分析的变量。从源变量框中选择要分析的变量放入Dependent List窗口。

(3)Factor List:分组变量窗口。Explore除了对样本的总体情况进行分析之外，还提供了分组分析的结果，根据Factor List中的变量取值，在结果中输出分组结果。如果不进行分组数据的分析，则无须选择变量放入Factor list窗口。

(4)Label Cases by:选择标识变量。使用该变量值标识各观测量。一般不用此功能。

(5)Display:结果显示。Display是输出结果显示的内容。

①Both:输出图形和描述统计量，这是系统默认选项。选择此项后，激活Statistics和Plots对话框，进一步进行选择。

②Statistics:输出描述统计量。选择此项激活Statistics功能按钮。

③Plots:输出图形。选择此项激活Plots功能按钮。

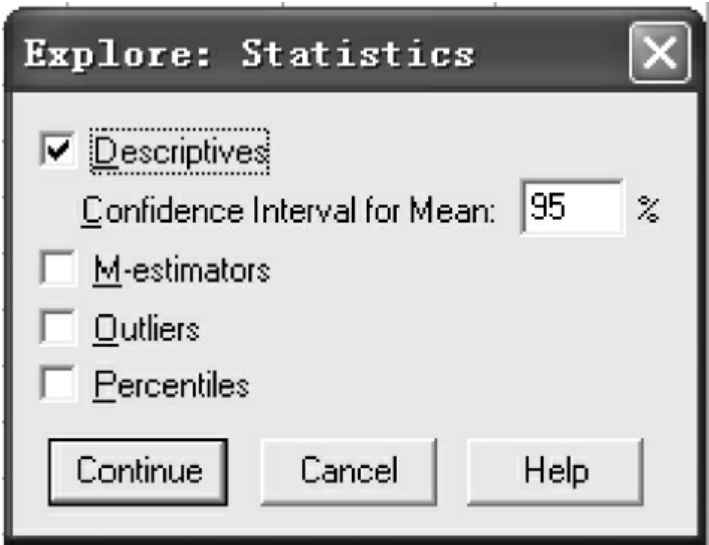
图10-11　Statistics统计量

(6)Statistics:描述统计量。

Statistics列出了主要的统计分析量，包括以下几个方面:

①Descriptives:输出主要的基本描述统计量，平均值、众数、5%的调整平均数、标准误差、方差、标准差、最大值、最小值、范围、四分位数、峰度、偏度及其标准差。这是系统默认的统计量。

Confidence Intervals for Mean，即均值的置信区间，在参数框中输入不同的置信度，选择范围从1%到99%，常用的有90%，95%和99%。95%是系统默认值。

②M-estimators:SPSS软件在对数据进行方差齐性检验时，不会只依据一个指标进行检验。M-estimators是最大似然比的稳健估计量。一般来说，最大似然比的稳健估计量可以很好地替代平均值和中位数，它受奇异值的影响较小。当数据分布均匀，或者当数据中存在极端值时，M-estimators可以给出比均值或中位数更合理的估计。这是因为依据均值、标准差等进行的方差齐性检验是建立在数据分布呈正态的前提下进行的，而中位数、全距、M估计等统计量在进行方差齐性检验时可以不依靠数据的正态分布。

M估计在计算过程中仍然把极端值包括在内，但对观测量赋予了不同的权重，权重的大小随观测值距离分布中心的大小而定，极端值由于靠外比位于中心部位的数据给予较小的权重。M估计值通常有Huber、Andrew、Hampel和Tukey四种，这四种方法都可以取代均值和中位数。其中Huber估计对近似于正态分布的数据的效果最好。

③Outliers:输出五个最大值与最小值，并在输出窗口标明为极端值。

④Percentiles:输出显示5%，10%，25%，50%，75%，90%以及95%的百分位数。

(7)Plots:图形。在主对话框选择Both和Plots之后，可以点击Plots按钮，展开对话框。Explore提供的图形主要包括(见图10-12):

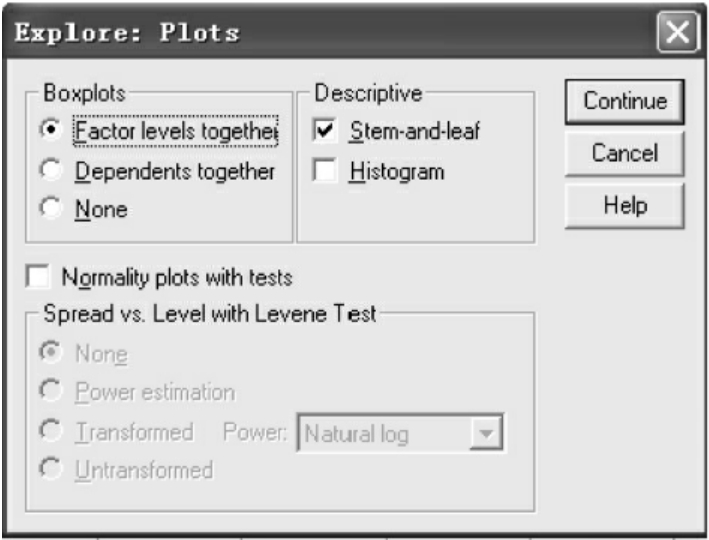
图10-12　Plots对话框

①Boxplots:箱形图。

●Factor levels together:每个因变量生成一个箱形图。可以比较同一因变量在分组变量值的不同水平上的分布情况；

●Dependents together:所有因变量生成一个箱形图。可以比较分组变量同一水平的各因变量值的分布情况；

●None选项，不显示箱形图。

箱形图各部分的含义以图10-13为例进行说明。

Ⅰ.矩形框是箱形图的主体，上中下三条线分别表示变量值的第75、50、25百分位数。变量50%的观测值落在这一区域。

Ⅱ.中间的纵向直线是触须线，上截止线是变量的最大值，下截止线是变量的最小值。

这两部分是排除了奇异值和极端值的变量取值，称为本体值。

Ⅲ.奇异值用“0”标记，分大小两种。箱体上方用0标记的点表示变量值超过了第75个百分位数与第25个百分位数差值的1.5倍，箱体下方用0标记的点表示变量值小于第75个百分位数和第25个百分位数差值的1.5倍。

Ⅳ.极端值用“*”表示，上极值点的变量值超过了第75个百分位数与第25个百分位数差值的3倍。下极值点值小于第75个百分位数与第25个百分位数差值的3倍。

②Descriptive:描述统计。

●Stem-and-leaf:茎叶图。这是默认选项。用来说明变量取值的基本情况。

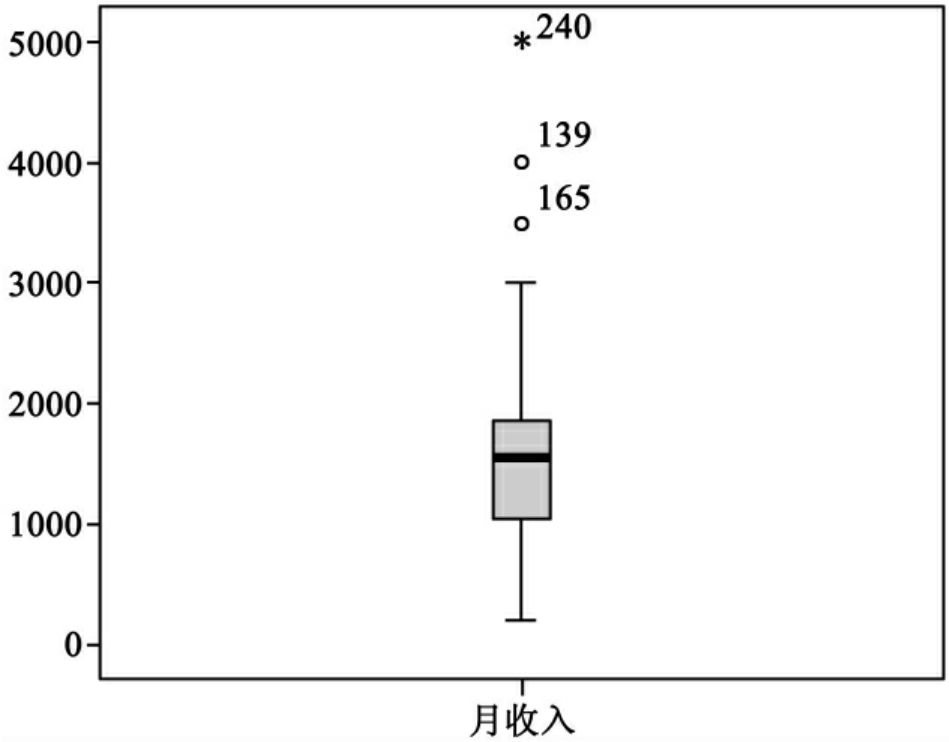
图10-13　箱形图各部分

茎叶图的结构见图10-14。

图10-14　收入的茎叶图

茎叶图从左到右分成三大部分:频数、茎和叶。茎表示数值的整数部分，叶表示数值的小数部分。每行的茎和每个叶组成的数字乘以茎宽，即为茎叶所表示的实际数值的近似值，即(茎、叶)×茎宽。如上茎叶图给出的信息是每个叶表示一个个案，茎宽为1000，如频数是8的一行，茎为2，这行的叶为22222222，这些元素表示这一行的8个个案的月收入都是2.2×1000=2200元。

●Histogram:直方图。

③Normality plots with tests:输出显示正态概率与离散概率图。同时输出Kolmogorov-Smirnov显著性水平。如果观测量不超过50，则输出Shapiro-Wilk统计量。

④Spread vs Level with Levene Test:分散—层次图及其检验。对分散—层次图来说，同时输出回归直线斜率及方差齐性的Levene检验。如果没有指定分组变量，则此选项无效。

Spread vs Level图中每个点的坐标分别是:每个箱图的四分位差、全距、中位数取自然对数为底的值。在显示此图形的同时还输出回归方程斜率及为使方差齐性的Levene稳健的估计量，也就是说为了使两个方差相同，对数据进行幂转换的幂值。图10-15(a)为箱形图，图10-15(b)为根据箱形图所得的Spread vs Level图。图10-15(b)中Slope为回归斜率，Power for transformation为进行数据幂转换的幂值，它们之间的关系为:幂值=1－回归斜率。

Levene检验方法最大的好处在于对两个样本的数据进行方差齐性检验时，不要求数据必须服从正态分布，Levene检验实际上也是一种方差检验，先计算出各个观测量减去组内均值的差，然后再通过这些差值的绝对值进行单因素方差分析。一般情况下，如果它的显著性水平小于0.05，就可以拒绝各因素方差相等的假设。

方差齐性检验提供了四种指标进行判断:

●None:不产生分散—层次图和方差齐性的检验，这是系统默认选项。

●Power estimation:转换幂值估计，对每一组数据产生一个中位数的自然范围的自然对数与四分位数范围的自然对数的散点图。为了使每组中的数据方差相等，对数据进行幂转换的估计。

●Transformed:对原始数据进行转换，在Power参数框中指定幂转换使用的幂值，包括:Cube三次方，Square二次方，Square root 1/2次方，Logarithm取对数，Reciprocal of square root－1/2次方，Reciprocal－1次方。

●Untransformed:不对数据进行转换。

(8)Options:其他统计量，指出了缺失值的处理方法(见图10-16)。

①Exclude cases listwise:剔除变量中带有缺失值的观测量；

②Exclude cases pairwise:剔除分组变量中带缺失值的观测量；

③Report values:分组变量中的缺失值被单独分成一组，输出频数表中也包括缺失组，点击Continue按钮回到上级对话框。

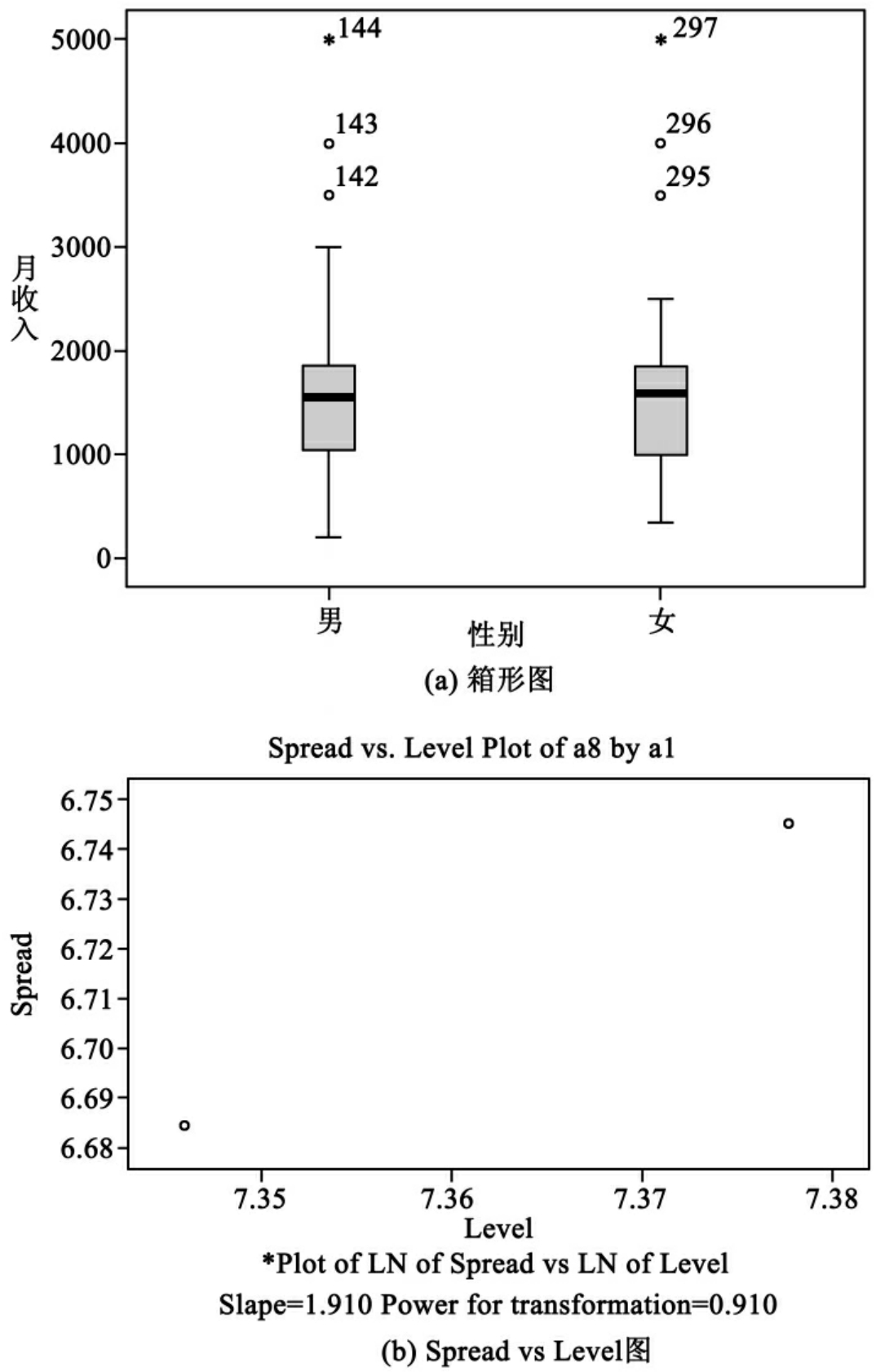
图10-15

(9)单击OK按钮，提交运行。在结果输出窗口中看到输出的结果。

2.实例分析

例4　以data10.1.1数据为例，分析不同性别工人的月收入情况。

打开数据，进行以下操作:

(1)点击Analyze→Descriptive Statistics→Explore，打开对话框。

图10-16　Options对话框

(2)选择“月收入(a8)”变量放入Dependent List窗口。选择“性别(a1)”变量放入Factor List窗口。

(3)Display栏中选择Both。

(4)打开Statistics窗口，选择Descriptives、M-estimatiors、Outliers。

(5)单击Plots按钮，打开Plots对话框，选择Boxplots栏中的Factor levels together项；选择Descriptives栏中的Stem-and-leaf选项；选择Normality plots with tests选项；选择Spread vs level with Levene Test中的Power estimation项。单击Continue按钮。

(6)单击OK按钮，提交运行。在输出结果窗口看到如表10-5至表10-9和图10-17的结果。

表10-5　统计概要

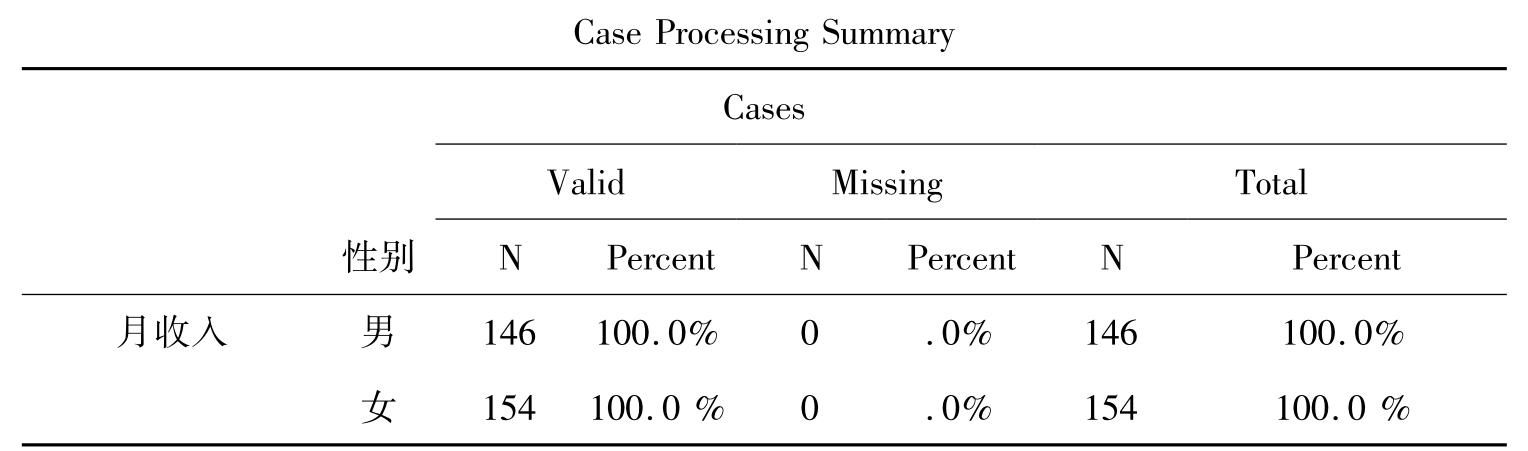
表10-5显示的是分析样本的基本情况，其中男性146人，女性154人。

表10-6　月收入的描述统计

表10-6分两组分别给出了男性和女性月收入的统计结果，包括(1)Mean(均值)；(2)95%Confidence interval for Mean(均值95%的置信区间)；(3)5%Trimmed Mean(5%的调整平均数)；(4)Median(中位数)；(5) Variance(方差)；(6)Std.Deviation(标准差)；(7)Minimum(最小值)；(8)Maximum(最大值)；(9)Range(全距)；(10)Interquartile Range(四分位数间距)；(11)Skewness(偏度)；(12)Kurtosis(峰度)。

表10-7　M估计值

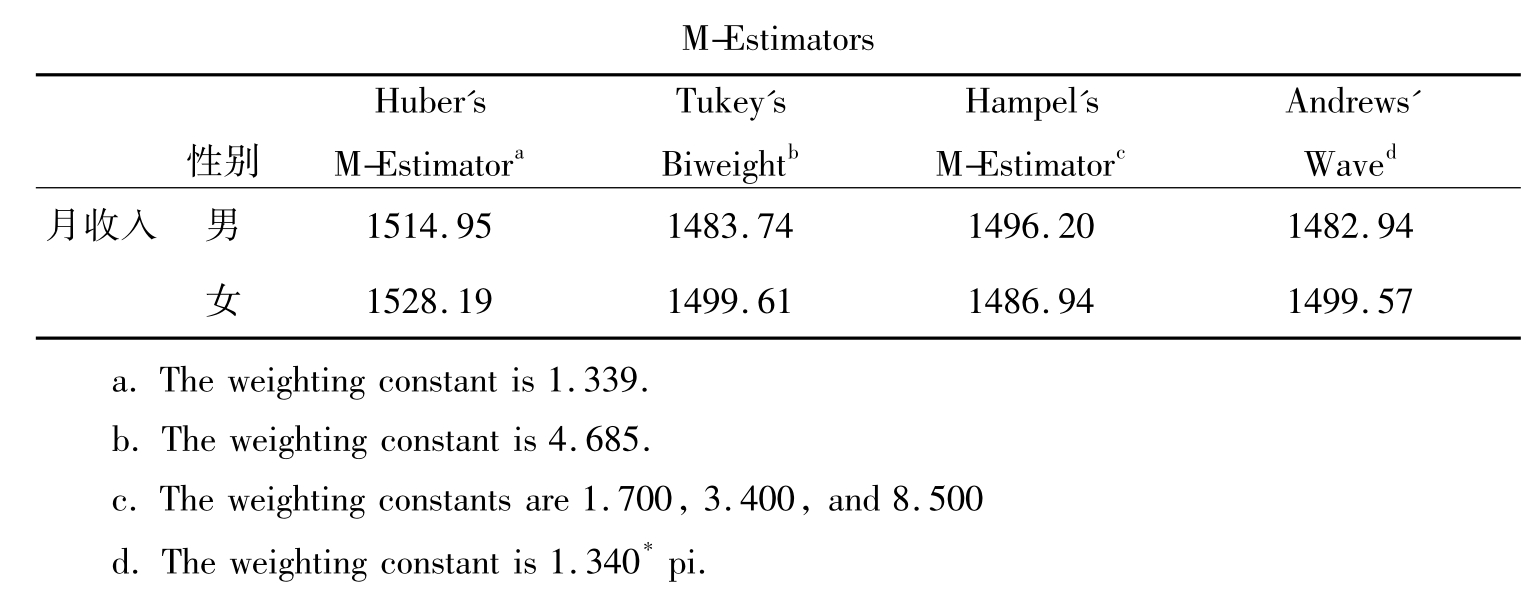
表10-7的结果是使用四种不同的方法计算出的M的估计值，它们的值与表10-6的均值相比要小一些，这是因为均值受到极值的影响。表下的a、b、c、d分别说明了四种加权的常数。

表10-8　变量的极值

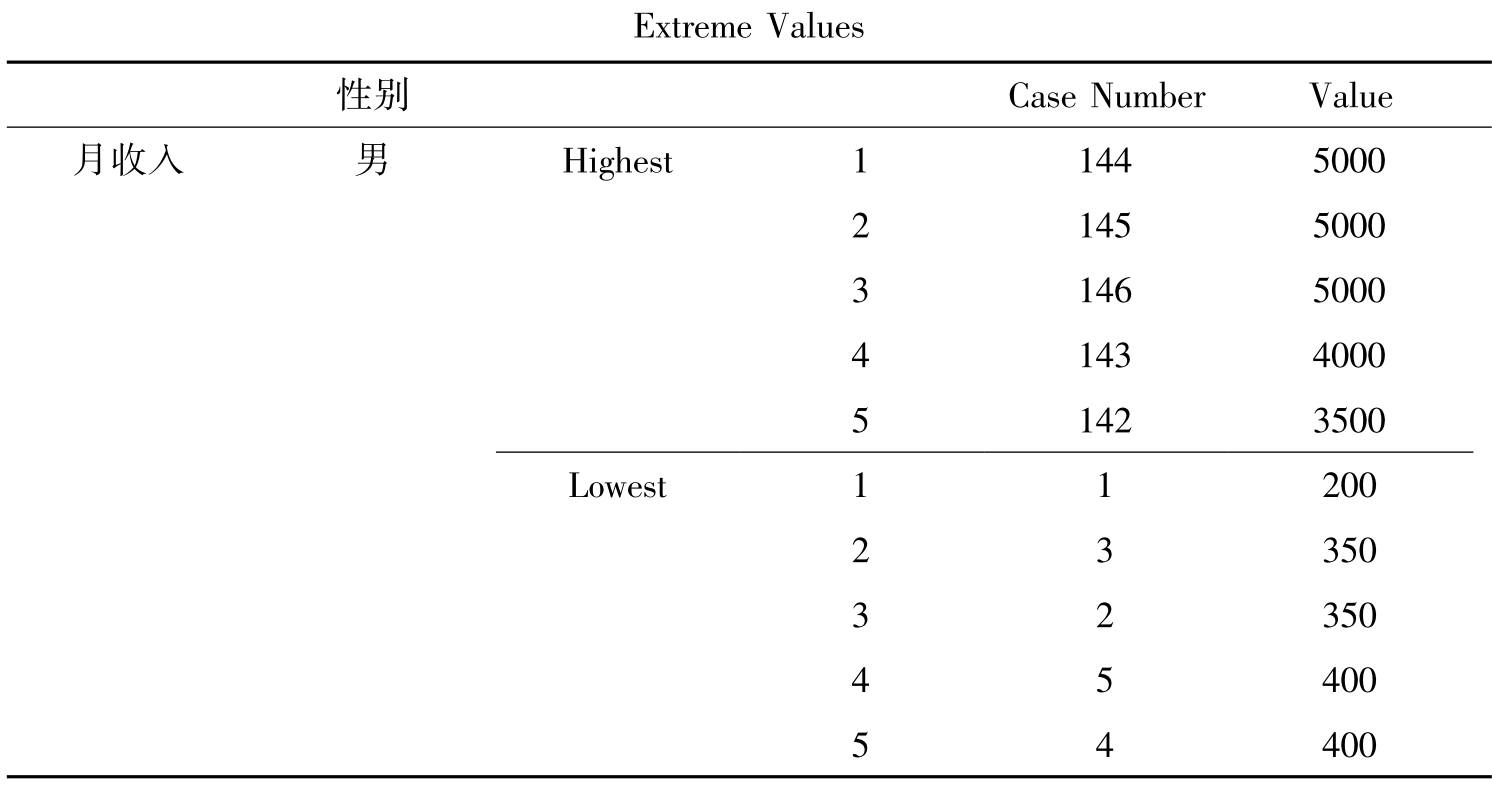
续表

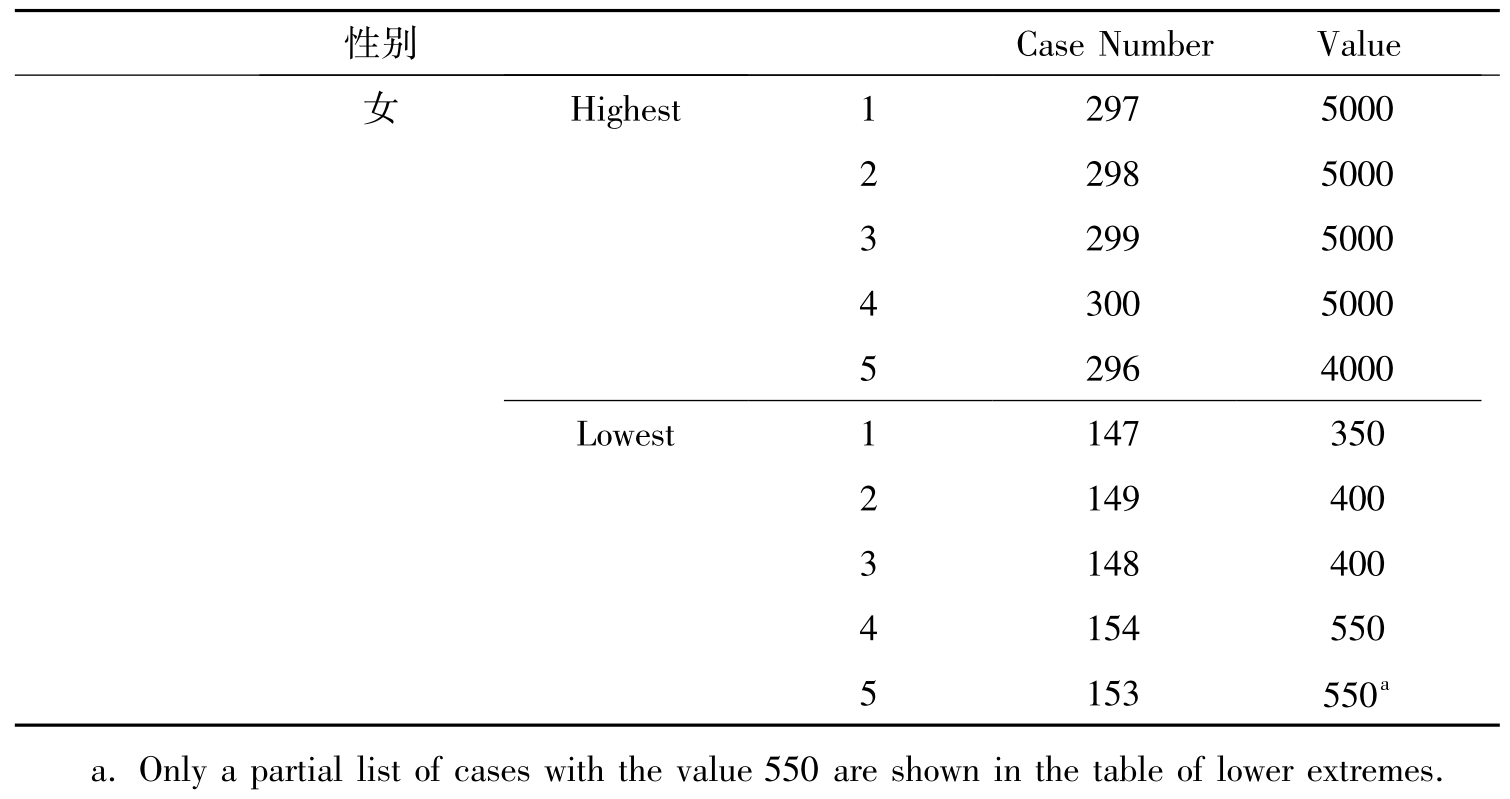
表10-8分别列出了男性和女性收入最高和最低的5个值的个案编号和具体取值。

表10-9　方差齐性检验

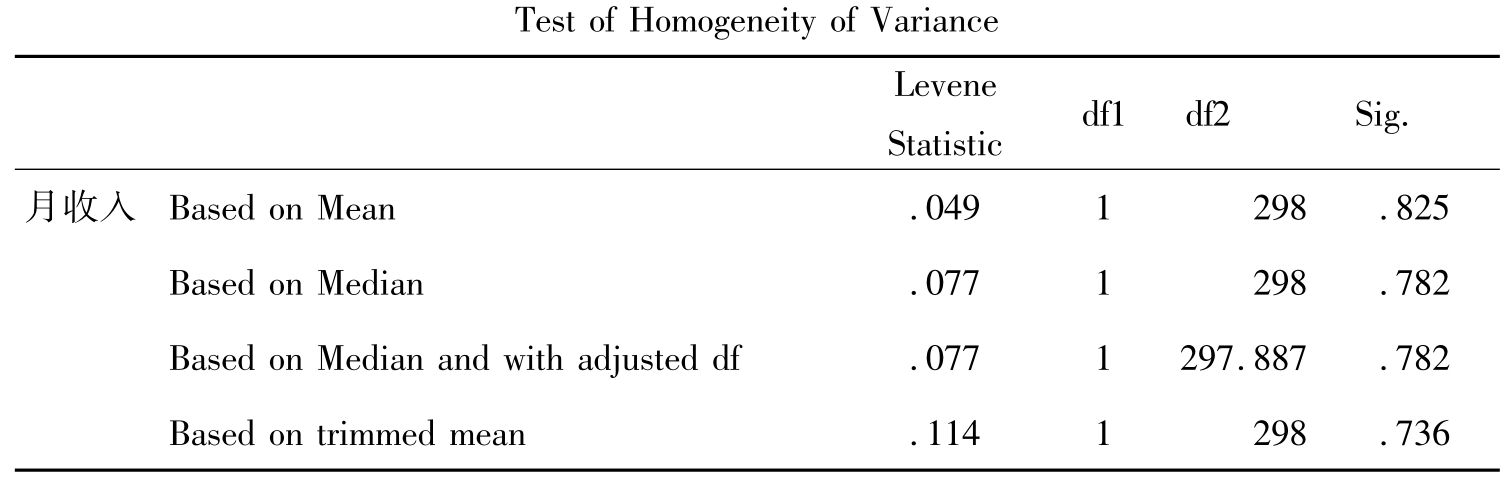
方差齐性检验的是男性和女性组是不是满足方差相等的假设。输出的结果是根据均值、中位数、调整自由度的中位数和调查均值四方面的方差齐性检验，检验的结果包括Levene统计量，自由度1，自由度2和显著性水平值。由于各指标所得的显著性水平值都大于0.05，所以不能拒绝虚无假设，也就是说两组的方差相等。

图10-17的(1)和(2)分别显示的是男性和女性月收入的茎叶图，具体分析见图10-14。

图10-18(1)和(2)显示的是男性月收入的正态概率图(女性略)。其中的斜线是正态分布的标准线。散点图的各点组成的曲线接近于直线，数据分布就接近于正态分布。从图(1)可以看出除了少量的奇异值外，大量的散点集中在斜线附近，可以看做近似于正态分布。图(2)的离散正态概率图可以看出，大多数的散点落在一条通过零点的直线周围，分布的散点并没有形成明显的曲线，也可以看出模型近似于正态分布。

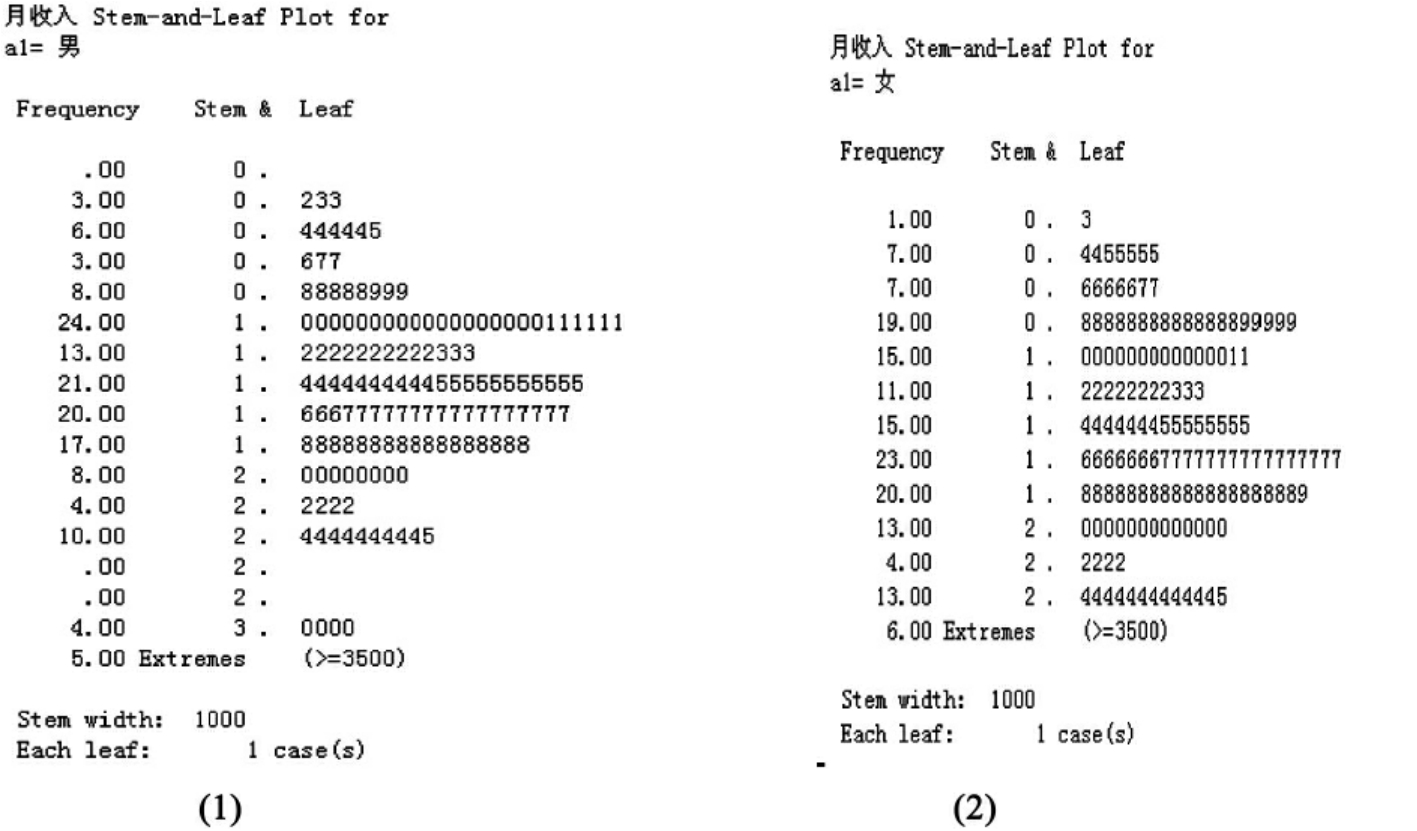
图10-17　男性、女性月收入的茎叶图

图10-19是按性别分组的月收入变量的箱形图，从中可以看出男、女月收入的差异，它们的极端值及编号。

图10-20是男女月收入的分散—层次图，数据进行幂转换的值为0.910，两点的斜率为1.910。

四、多选变量的频数统计(Multiple Response Frequencies)

多选变量是包含了多个答案的变量，要求被调查者在回答时进行多项选择，多项选择题可以在SPSS数据输入时做成多个内容相同的变量。多选变量在进行分析时，不仅希望知道某些变量在选择中的顺序，如在第一选择、第二选择或第三选择中分别被多少人选过(通过Frequencies解决)，还希望知道某些选项在多次选择中被选择的总次数和频率，这时就需要进行多选变量分析(Multiple Response→Frequencies)。多选变量在数据录入时有两种形式(见数据data10.1.4):一是根据重要性进行排序，如对大学生每月消费的主要项目按金额多少的排序(变量d03x1，d03x2，d03x3)；二是在没有顺序排列或不确定选择几个选项时，一般采用“0，1”编码的形式，即选择了此项在录入数据时录为“1”，没有选择则录“0”，如对大学生闲暇时间的休闲娱乐方式的研究(变量c2x1～c2x11)。一定要注意的是把这些变量设置为数值型变量，否则无法进行多选变量的分析。多选变量分析的基本过程分两步进行。第一步是将多选变量生成一个新变量；第二步是对新生成的变量进行分析。

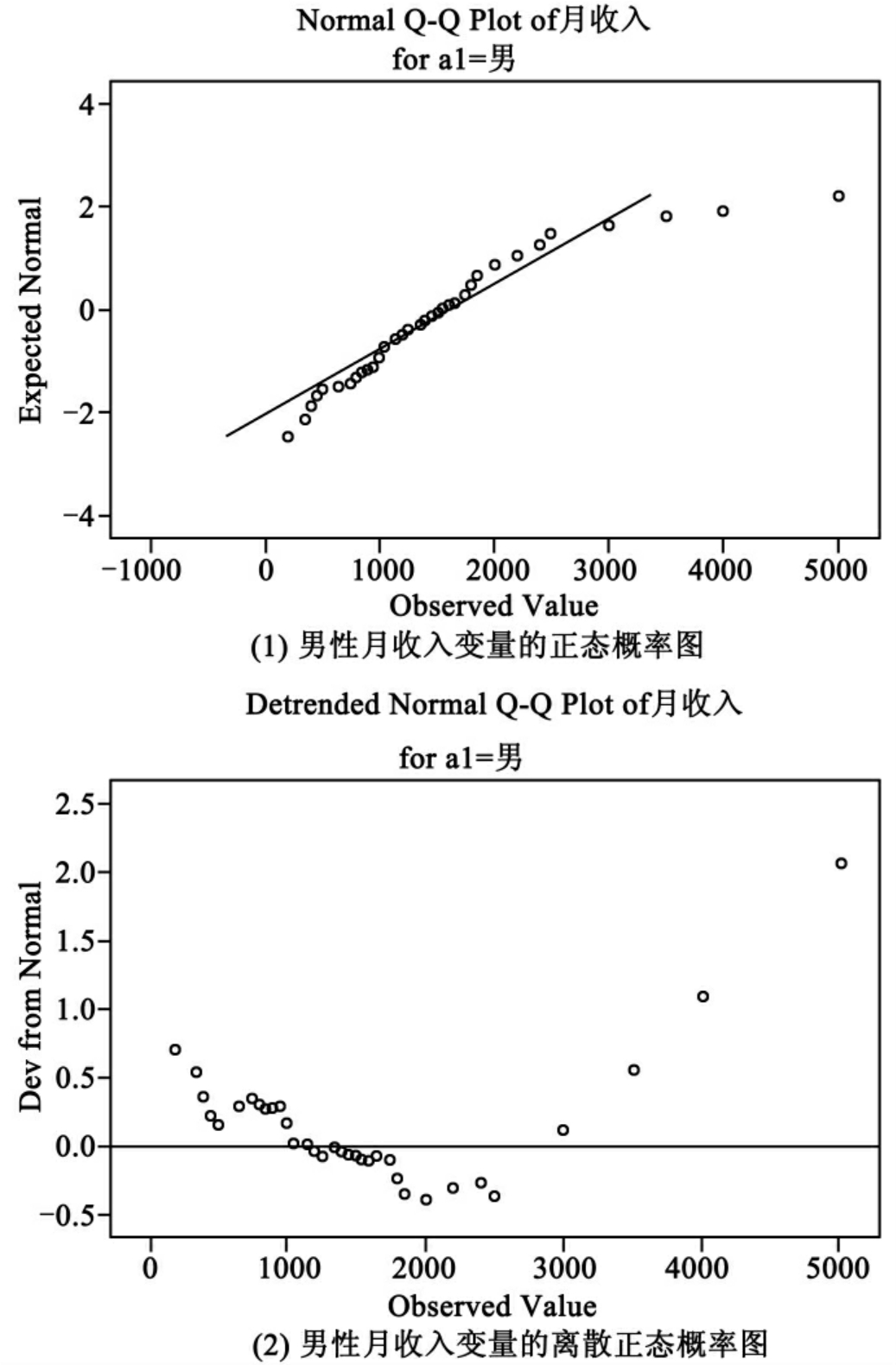
图10-18

1.多选变量的分析过程

多选变量的分析过程一般分为两步，具体的过程如下:

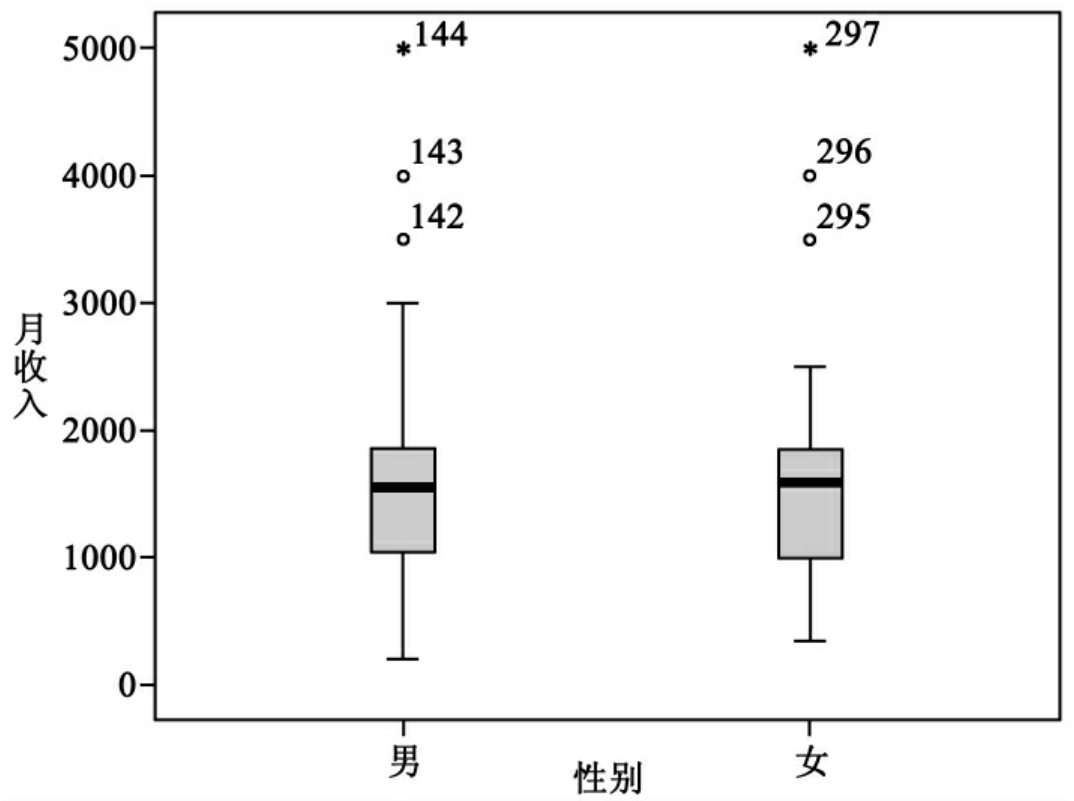
图10-19　月收入变量的箱形图

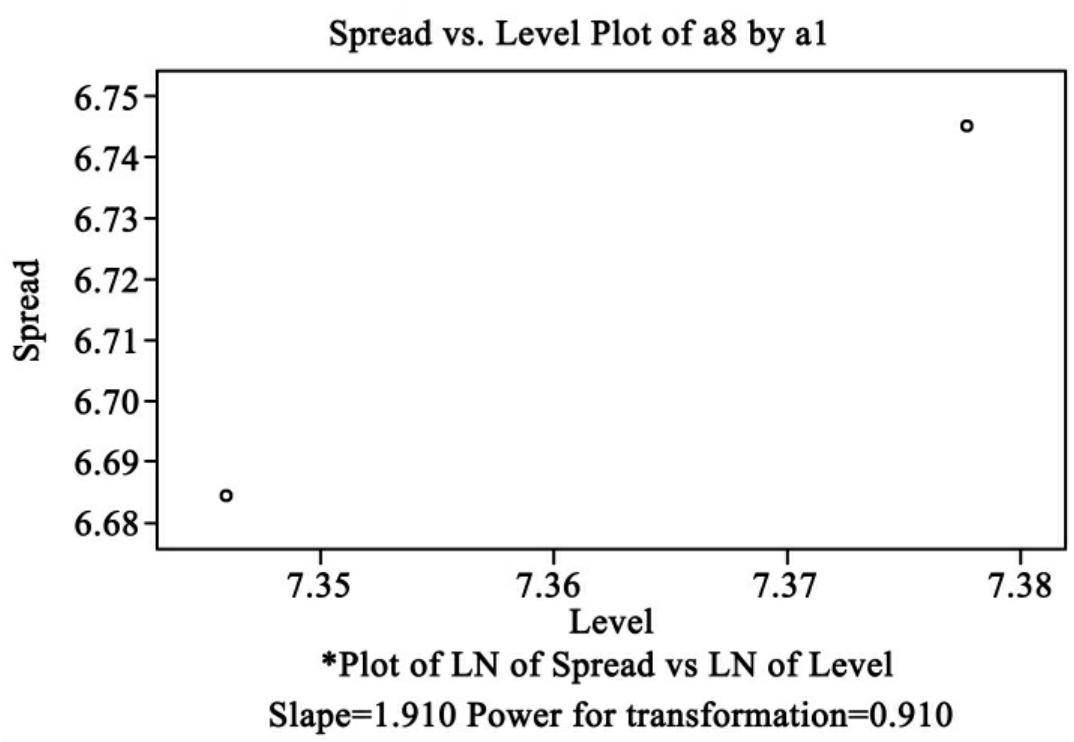
图10-20　月收入变量的分散—层次图

用多选变量生成新的变量。

执行以下操作:

①点击Analyze→Multiple Response，打开如图10-21的对话框。

在Multiple Response菜单中，下面两项灰色的是隐含的，只有Define Sets(定义多选变量)是可以用的。点击Define Sets，打开对话框，见图10-22。

图10-21　多选变量分析对话框

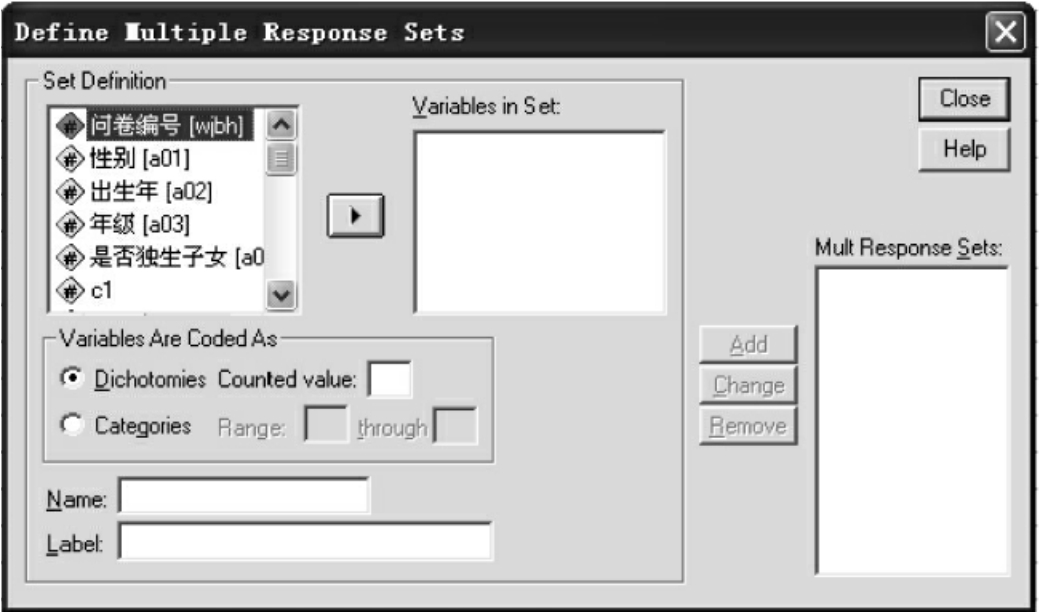
图10-22　Define Sets对话框

其中，Set Definition窗口列出的是源变量。Variables in Set窗口是被选入模块的变量。在Set Definition窗口中选择将要进行分析的多选变量，使之进入Variables in Set窗口。

②Variables Are Coded As:确定多选变量的值。Variables Are Coded As是定义多选变量的值的选项栏:

●Dichotomies:二分变量选项，将要统计的结果输入“Counted value”框中，如大学生休闲娱乐方式变量，要统计的是大学生休闲时间一般做什么，在数据录入时，参与某项活动的录为“1”，没有参与的为“0”，所以在统计的时候输入“1”。一般研究的是被调查者是否有此行为，选择要统计的变量一般为1；如果选择0，则统计的是不作为的结果。

●Categories:多数值变量选项，适应多项限选题编码。选择此项可统计某一值域范围内变量的结果，范围以外的值将被视为缺失值。将多选变量的取值范围输入到后面的两个窗口中，前一个窗口输入范围的低值，后一个窗口输入范围的高值。

③Name，Label:确定新生成变量的变量名和变量名标签。在Name窗口中输入新生成变量的变量名。在Label窗口中输入新生成变量的变量名标签。

④上述选项完成以后，便激活了Add按钮。单击Add按钮，把定义好的变量添加到Mult response Sets(多选变量集)窗口中(见图10-23)。

图10-23　多选变量的设置

⑤单击Close按钮完成多选变量集的定义。此时，系统已生成了一个新的变量，但这个变量并不在数据窗口中显示出来。

2.多选变量的频数分析

上述用多选变量生成新变量的工作完成以后，执行下述操作:

①点击Analyze→Multiple Response，拉出二级菜单，见图10-24。

经过前面的设置，原来隐含的Frequencies和Crosstabs命令已被激活，即可以对多选变量进行频数分析和交叉表分析。单击任何一项，打开相应的对话框。

②Frequencies:打开频数对话框，见图10-25。

图10-24　设置完多选变量的统计窗口

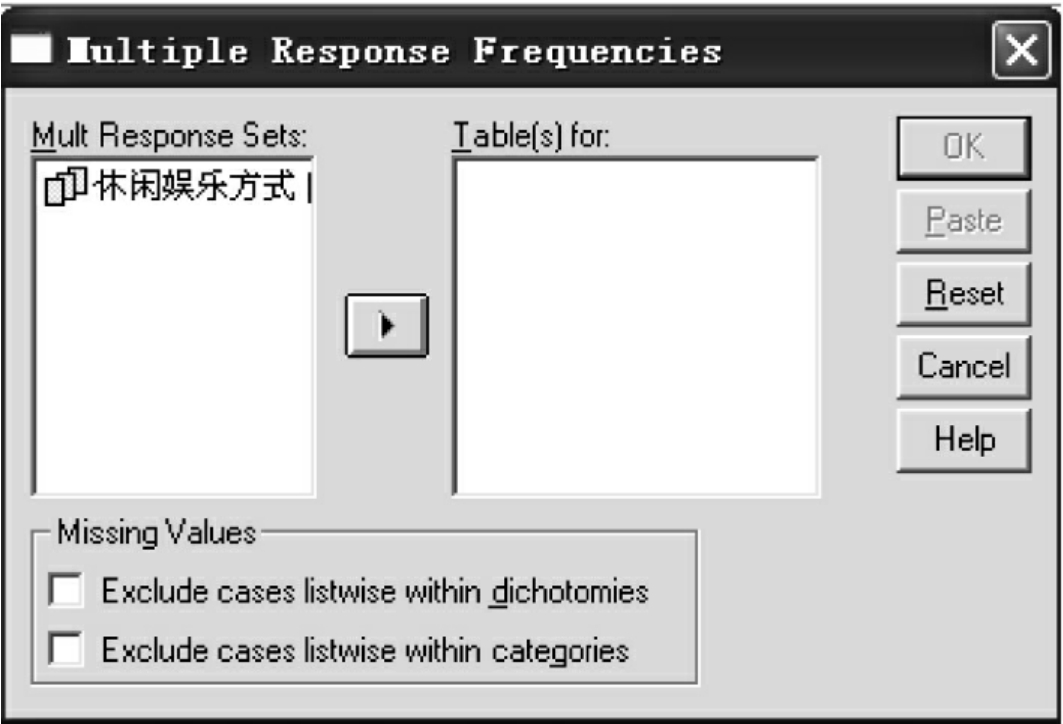
图10-25　多选变量Frequencies分析窗口

其中，

●Mult Response Sets窗口中的变量即是多选变量生成的新变量；

●Table(s)for窗口中的变量是要分析的变量；

●Missing Values:处理缺失值方法的选项栏。

Ⅰ.Exclude cases listwise within dichotomies:排除二分变量中的缺失值。

Ⅱ.Exclude cases listwise within categories:排除多项取值变量中的缺失值。

③确定要分析的变量。选择Mult Response Sets窗口中的变量，放入Table(s)for窗口。

④单击OK按钮，提交运行。在输出结果窗口中输出频数分布表。

3.实例分析

例5　以数据data10.1.4大学生闲暇娱乐变量为例分析大学生的闲暇娱乐方式。

具体的分析过程如下:

(1)点击Analyze→Multiple Response，打开如图10-21的对话框。

(2)点击Define Sets，在Set Definition中选择“c2x1”至“c2x11”变量放入Variables in Set窗口。

(3)由于被分析的多选变量采用的是“0，1”编码的形式，只有0和1两个合法值。所以选择Dichotomies Counted value选项，在窗口中输入“1”。

(4)在Name窗口中输入“c2”作为新生成变量的变量名，变量名标签为“休闲娱乐方式”。单击Add按钮，将新生成的变量“c2”添加到Mult Response Sets窗口中。

(5)单击Close按钮，关闭该对话框。系统已生成了一个名为“c2”的新变量。

(6)点击Analyze→Multiple Response→Frequencies，打开如图10-25的对话框。

(7)选择Mult Response Sets窗口中的变量“c2”。将变量“c2”放入Table(s)窗口，激活OK按钮。

(8)单击OK按钮，提交运行。系统打开输出窗口，得到表10-10和表10-11的结果。

表10-10　统计概要

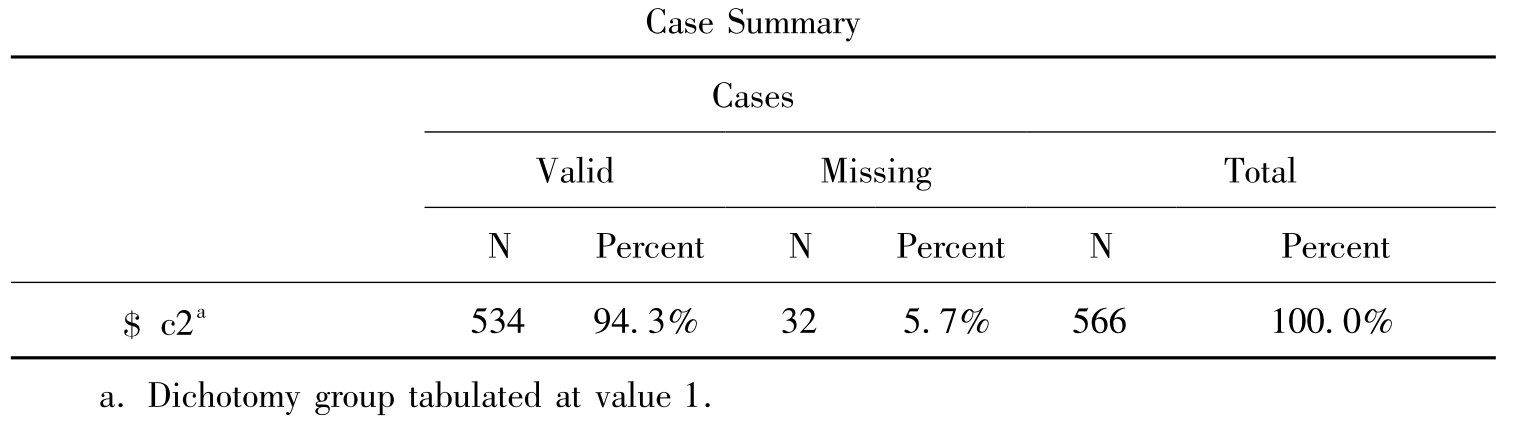
表10-10　指出参与统计的有效样本数是534，缺失样本数是32，样本总数是566。

表10-11　多选变量的分析结果

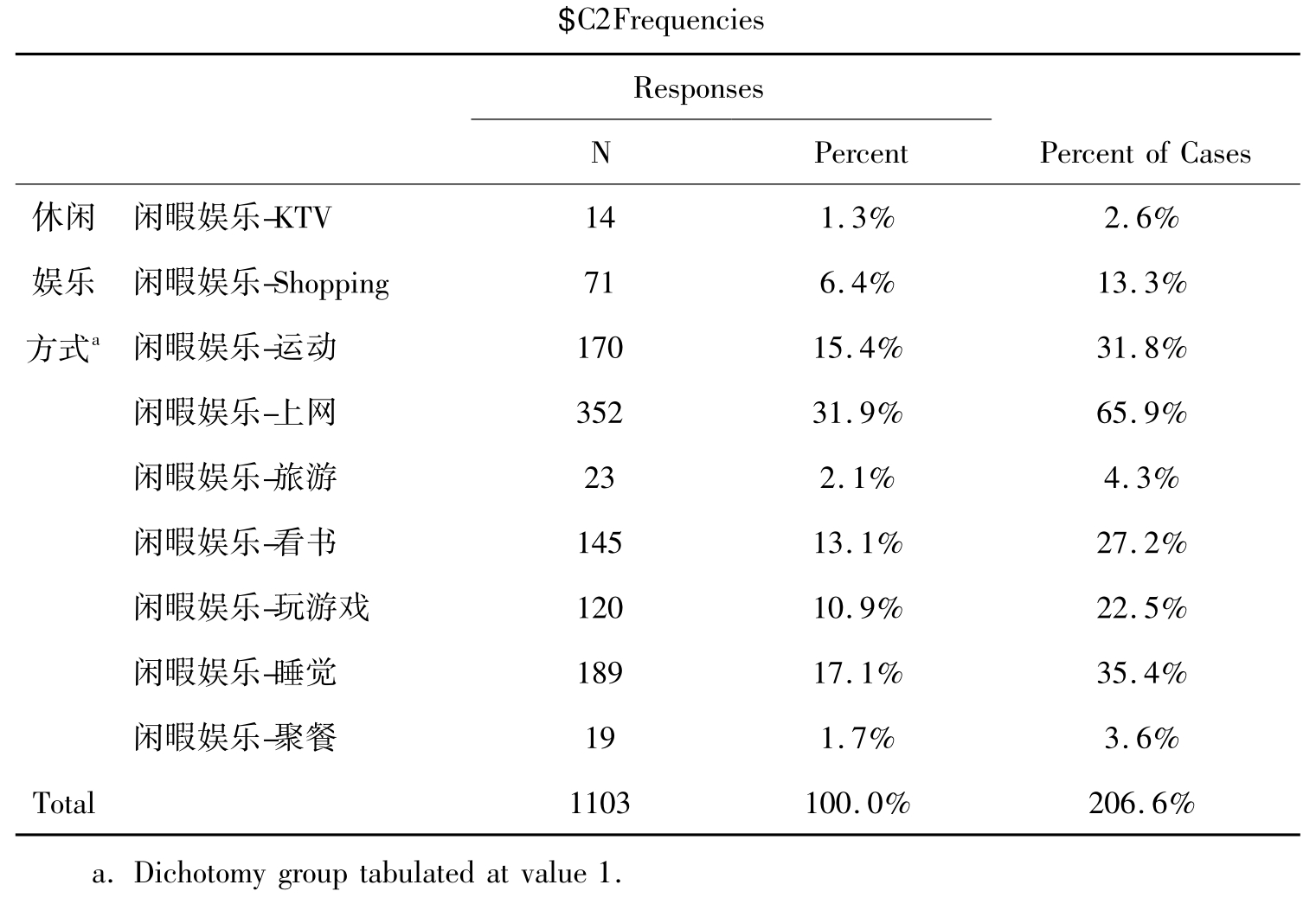
表10-11中Response指的是回答的情况，N的数据是每个选项被回答的次数，Total是回答的总次数。Responses下面的Percent是以回答次数作为分母的百分比，Percent of Cases是以个案数为分母的百分比。由于每个人都可以做多项选择，所以以个案数为分母的百分比要大于回答次数作为分母的百分比，并大于100%。从表中可以看出，534个个案作了1103次选择。表下的说明指出统计结果是变量取值为1的结果。