炉膛传热计算的相似理论法

时间：2022-10-23 百科知识版权反馈

【摘要】：由前可知，炉膛传热量的确定等价于炉膛出口烟温的确定。它表示炉膛换热能力与炉膛为黑体时的换热能力之比。在相同的炉膛容积热负荷qV的条件下，改变炉膛的形状系数，可以计算出不同的炉膛出口烟温。但当有效辐射层厚度减小时，会使炉膛面积及相应的有效辐射面积成正比地增加，从而使受热面的吸热量增加，炉膛出口烟温降低。层燃炉炉膛形状的变化范围比较大，有效辐射层厚度的变化远超过20%，炉膛黑度的变化约在50%左右。

9.2.5　炉膛传热计算的相似理论法

1.炉内温度场分布规律

研究炉内温度场分布规律的目的就是确定火焰的平均温度T_hy。

前面讲过，火焰及烟气的温度在其行程上的变化是剧烈的，但影响炉内温度场沿炉膛高度的变化有许多因素，例如，燃料特性，燃烧方式，受热面的结构特性等。但试验表明，对于有相当高度而四周布满水冷壁的炉膛，炉内温度场具有类似性，并且可表示为

式中：T_ll为理论燃烧温度；X为相对火焰高度，X＝；L为火焰的总高度（燃烧器中心到出口中心）；x为距燃烧器中心的火焰高度；α，β为考虑传热，燃烧对火焰温度影响的经验系数。

在式（9.76）中令X＝1，得到炉膛出口无因次温度的四次方：

将式（9.76）从0到1积分，可得到炉膛火焰温度四次方的平均值：

最高温度点的位置由

来确定。得

由于，及X_m均为α和β的函数，联立后消去α和β，得

此函数关系画在图上，即得到图9.7。可以看出，X_m不变时，lgΘ_hy与lgΘ″_l呈线性关系。因此有

图9.7　与Θ″_l及X_m的关系

m和n均是X_m的函数，即

截距近似为0，即lg≈0，于是，m≈1。n实际上是X_m为不同值时，直线的斜率，从图中可以大致得到

0.4＜n≤1.0

最后，火焰平均温度为

即

2.炉膛黑度

火焰的有效辐射

炉壁对火焰的有效辐射

而

将q_yx1和q_yx2代入并整理后，得

于是，式（9.85）成为

对于火床炉，炉排上的炽热煤层也参与辐射换热，情况更为复杂。假定燃烧层的黑度为1，燃烧层的温度与火焰温度相等，求解得：

式中：ρ为炉排面积R与不包括R的炉膛总壁面积F_bz之比。即

3.火焰黑度

从传热学的观点，将火焰作为灰体，则

式中：s＝3.6，称s为有效辐射层厚度，V为炉膛容积，F_l为炉壁面积；p为炉膛压力，一般取p＝0.1MPa；K为火焰辐射减弱系数，是火焰中各种辐射介质的减弱系数的代数和，单位是1/（m·MPa）

燃用气体、重油的火焰中，主要辐射介质是三原子气体及炭黑。燃用固体燃料的火焰中，除三原子气体外，还有灰粒子及焦炭粒子。

一般将上述两种情况分开处理。

燃用气体或液体燃料时，火焰的黑度可认为由火焰中的发光部分的黑度a_fg和不发光部分的黑度a_bfg组成。

即

式中：m为发光部分在火焰中所占份额，它取决q_V。当q_V≤400kW/m³时，m＝0.1（气体）和m＝0.55（液体）；当q_V＞1200kW/m³时，m＝0.6（气体）和m＝1（液体）；当400＜q_V≤1200时，采用直线内插法确定。m的数值也可按图9.8来查取。

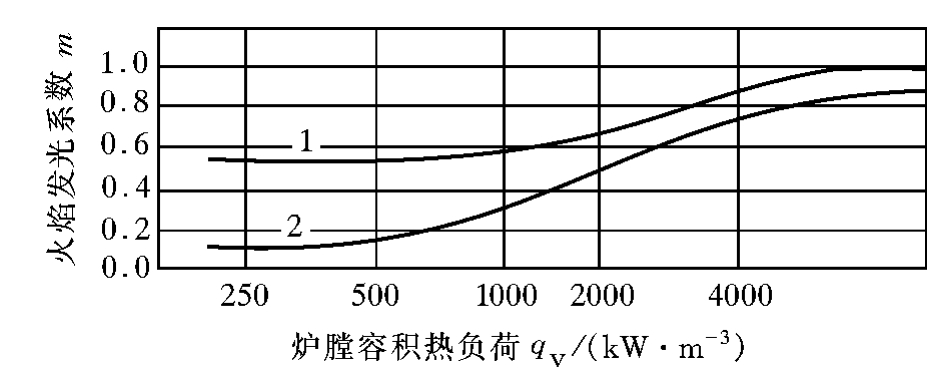
图9.8　火焰发光系数

1—重油；2—气体燃料

式中：r_q为火焰中三原子气体总的容积份额，r_q＝＋；k_q为三原子气体的辐射减弱系数，按式（9.3）计算；p_q为火焰中三原子气体总的分压力，p_q＝r_qp；k_th为火焰中炭黑粒子的辐射减弱系数。

因此

从该式中可看出：C/H越高，炭黑粒子的浓度就越高，k_th越大。α″_l越高，k_th越小，当α″_l＝2时，k_th＝0。T″_l越高，炉膛中C_mH_m分解的越多，k_th越大。

燃用固体燃料时

式中：ρ_y为烟气的密度，可取ρ_y＝1.3kg/m³；d_h为灰粒的平均直径，对层燃炉，可取d_h＝20μm，对煤粉炉，可取d_h＝16μm；μ_h为灰粒的无因次浓度

焦炭颗粒的辐射减弱系数k_j可取k_j＝10 1/（m·MPa）。x₁为考虑燃料种类影响的系数，对无烟煤和贫煤，取x₁＝1；对烟煤和褐煤，取x₁＝0.5。x₂为考虑燃烧方式影响的系数，对煤粉炉取x₂＝0.1；对层燃炉取x₂＝0.03。

4.炉膛出口烟温及其影响因素

由前可知，炉膛传热量的确定等价于炉膛出口烟温的确定。炉膛出口烟温的数值就决定着分配给炉膛的传热量的多少。

（1）前苏联“热力计算标准方法”

前苏联学者曾对炉内换热进行过大量而细致的工作。确定炉膛传热量的基本出发方程是热平衡方程Q_热平衡＝φB_jVC_pj（T_ll－T″_l）和由炉膛黑度确定的炉膛辐射换热量方程

由于

则

由以上两个方程可得

式中

这里Bo称为炉膛换热相似准则数或Boltzmann准则数。它表示炉膛换热能力与炉膛为黑体时的换热能力之比。

若能够确定m，n的数值，则从这个无因次方程可以进行炉膛传热的计算。如前面所述，m≈1。则

研究表明，n与燃烧及传热条件有关，不能依靠理论分析得到，统计分析大量的试验结果，

得

或者

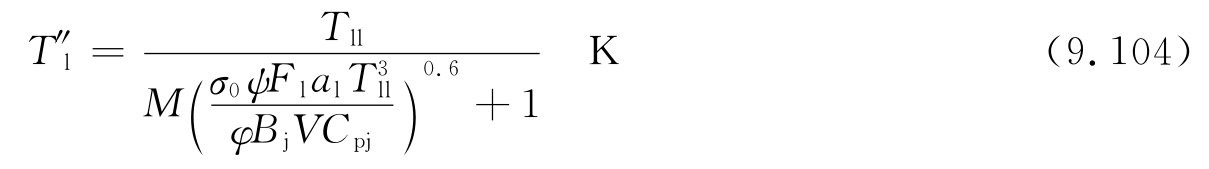
式中：M为经验系数，取决于火焰最高点的相对位置X_m，与燃料种类，燃烧方式有关。

M的数值可按下列经验公式来求得

表9.2　A、B的取值

式中：A、B为与燃料炉膛结构有关的经验系数，其值见表9.2。

X_m值按下式确定

式中：X_r＝为设置燃烧器的相对标高；h_r为燃烧器轴线离炉底或冷灰斗中腰线的设置高度，m；H_l为从炉底或冷灰斗中腰线到出口窗中位线的炉膛高度，m；ΔX为考虑到炉内最高温度的位置偏离燃烧器设置标高时的修正值。

ΔX的数值见表9.3。

表9.3　ΔX的数值

根据式（9.104）可以计算出炉膛出口烟温θ″_l或炉膛壁面积F_l。

当已知炉壁面积，需求炉膛出口烟气温度时：

当已知炉膛出口烟气温度时，需求炉膛辐射受热面H_f时：

或

以上就是前苏联《锅炉机组热力计算标准方法》1973年版本中关于炉内换热的主要内容。

（2）我国层燃炉热力计算方法^［6］

基本出发方程式

式中：T_pj为炉内烟气（火焰）的有效平均温度

式中：T_jr为绝热燃烧温度，即理论燃烧温度；n为反映燃烧工况对炉内温度场的影响。对抛煤机炉n＝0.6，对其它层燃炉n＝0.7；T_b为水冷壁管外结灰层表面温度。

式中：T_gb为水冷壁管金属温度，取为工作压力下水的饱和温度；ε为管外灰层热阻，取决于燃料性质及炉内燃烧工况，一般取为ε＝0.0026m²·℃/W；q_f为辐射受热面热流密度。

由于

变形后，有

进一步得

设m＝＝（εq_f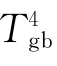＋）（考虑水冷壁结灰层表面温度对炉膛传热的影响），则

则

与热平衡方程Q＝φVC_pj（T_jr－T″_l）联立，得

由此，有

Bo为波耳兹曼（Boltzmann）准则数。

改写　T_pj＝为

即

m值对于层燃炉，当q_f＝474～1 186kW/m²时，对应一定的工质温度，可取为常数，有表图供查取。

表9.4　系数m的数值

系统黑度

式中：a_b为水冷壁黑度，一般可取a_b＝0.8。

表9.5　系数k和p的数值

式中：R为炉排有效面积；F_bz为炉膛不包括R的所有炉壁面积；x为水壁的平均角系数，x＝；F_l为炉壁总面积。

若已知Bo（＋m）及n，则可求得Θ″>_l。

为了便于工程计算，改写上式成为

对应于n、Bo（＋m）可由表9.5查得k，p之值，从而得到Θ″_l。

燃尽室的传热计算与炉膛类似，但

得

式中：a_y为燃尽室的烟气黑度。

最后解得

（3）影响炉膛出口烟温的因素

分析炉膛传热基本公式以及实际运行经验，有如下一些因素会对炉膛出口烟温有明显的影响：

①燃烧器型式及布置位置。燃烧器型式不同和布置在炉膛中的位置不同将会明显地改变炉内火焰中心的位置。例如，摆动式直流燃烧器一、二次风喷嘴上下摆动±20°时，火焰中心的高度将变化1.5～2.5m。当火焰中心提高时，θ″_l会提高。一般的摆动式直流燃烧器上下摆动幅度约±20～30°，这时炉膛出口烟温可增加或降低110～140℃。

对于多层布置的旋流式燃烧器，改变上下各排的燃烧器的热功率，也能使火焰中心抬高和降低，从而改变炉膛出口烟温。例如，一台2000t/h燃用褐煤的锅炉，当最上层一排燃烧器的热功率减到额定功率的40%时，炉膛出口温度由原来的989℃降低到952℃。

②受热面的多少。显然炉膛辐射受热面增加，将使炉膛出口烟温降低。

③炉膛形状系数。炉膛形状系数f为炉壁面积Fl与炉膛有效容积V之比。图9.9炉膛形状系数f与炉膛的H/d_dl的关系。H为炉膛的高度，d_dl为炉膛横截面的平均当量直径。在同样的炉膛容积和炉壁面积时，H/d_dl越大，f值越大，即炉膛的当量直径越小（或炉膛横截面积越小），炉壁面积越大。布置双面露光水冷壁也可以提高形状系数。

图9.10给出了一台220t/h燃油锅炉的炉膛容积热负荷与形状系数和炉膛出口温度的关系。在相同的炉膛容积热负荷q_V的条件下，改变炉膛的形状系数，可以计算出不同的炉膛出口烟温。由图可见，q_V不变时，随着形状系数的增加，炉膛出口烟温不断降低。我国的研究人员对一些75t/h的中压煤粉炉、220t/h的高压煤粉炉及420t/h的超高压煤粉炉进行炉膛传热试验时也发现，炉内温度场的分布与炉膛的几何特性H/d_dl有明显的关系。

炉膛形状对炉膛黑度也有一定的影响。形状系数大的炉膛，有效辐射层厚度较小，因而火焰的黑度和炉膛黑度也较小。这样必然降低火焰的辐射能力，使炉膛出口温度提高。在实用的室燃炉炉膛中，炉膛形状的变化有限，有效辐射层厚度的变化一般不超过20%，由此而引起的炉膛黑度的变化亦不超过3%，所以对炉膛出口烟温的影响很小。但当有效辐射层厚度减小时，会使炉膛面积及相应的有效辐射面积成正比地增加，从而使受热面的吸热量增加，炉膛出口烟温降低。

图9.9　炉膛形状系数f与炉膛的H/d_dl的关系

实线表示无双面露光水冷壁的炉膛；

虚线表示有双面露光水冷壁的炉膛

层燃炉炉膛形状的变化范围比较大，有效辐射层厚度的变化远超过20%，炉膛黑度的变化约在50%左右。这对炉膛传热有着显著的影响，特别是燃用劣质煤、采用低而长的后拱时，炉膛形状复杂，大大地降低了炉膛的传热能力，提高了炉膛出口烟温。但是，层燃炉的形状变化往往着重于改善燃料的着火和燃尽等燃烧工况的需要。

图9.10　炉膛出口烟温与形状系数的关系

总之，炉膛形状对炉膛传热过程是有影响的，而且主要反映在对炉内温度场的影响上。

在实际运行条件下，许多因素都会偏离锅炉的设计工况，这对炉内的传热和炉膛出口烟温会有很大的影响。

④受热面结渣和积灰程度的变化。在燃用固体燃料以及重油等液体燃料时，炉膛的水冷壁管外表面发生结渣或积灰现象是不可避免的。而且积灰或结渣随运行工况的变化，其严重程度也有所不同。例如，运行过程中由于煤的可磨性系数的变化或制粉系统热平衡状态的不同均会改变送入炉膛中的煤粉细度，当煤粉细度增加时，煤粉颗粒变粗，煤粉在炉膛内的燃尽时间相对增加，而大粒度未及时燃尽的煤粉很容易被抛到烟气流速较低的炉壁面上。如果这些颗粒的灰呈粘性状态，则必然会粘附到受热面上，并逐渐发展成大的渣块。因此，过粗的煤粉加剧了结渣的程度，恶化了炉内的传热过程，造成炉膛出口烟温的升高。

又如，在运行过程中一次风风温的变化会改变煤粉火焰的着火距离。一次风温提高，煤粉着火提前，着火距离缩短，使燃烧器出口附近的燃烧强度增加；火焰温度升高，容易造成燃烧器区域受热面的结渣。燃烧器区受热面的结渣不仅影响到受热面的传热能力，引起炉膛出口烟温的升高；更为严重的是可能烧坏燃烧器，影响到炉内空气动力场，致使火焰中心偏斜。若一次风气流形成一股扑壁气流时，那末炉膛内的结渣现象更加严重。

特别需要强调的是，受热面的结渣污染和传热过程相互作用是一个不稳定的过程。受热面污染后，炉内传热过程减弱，炉膛的烟气温度水平提高，从而使更多的灰粒处于粘性状态。更容易在受热面上结渣，加剧了受热面的污染。这个过程在炉膛中很难达到平衡状态。因此，炉膛出口烟温不断升高，严重地危及锅炉机组的经济安全运行。

⑤锅炉负荷变化。运行中锅炉负荷的变化会引起燃料消耗量的变化，炉内火焰的温度场的形态和数值也将随之而变。炉内温度场的变化必然导致炉内辐射换热量的改变。但是炉内辐射换热量的变化幅度并不等同于燃料量的变化幅度。根据试验，锅炉负荷从半负荷状态变化到额定负荷时，负荷增加100%，炉内火焰平均温度增加约200℃，炉内辐射换热量增加70%左右。这说明炉内辐射换热量的变化率小于锅炉负荷的变化率。所以，当锅炉负荷增加时，炉膛出口烟焓必然增加，炉瞠出口烟温升高。

⑥过量空气系数的变化。过量空气系数的变化对炉内温度场的影响是很显著的，其原因主要基于下述几个方面：

过量空气系数增加，送入炉内的吸热性介质增多，烟气的热容量增大，火焰中心的温度水平下降，火焰中心的位置上移。如果过量空气系数α″_l增加较多，送入炉膛的空气被加热到火焰的温度所吸收的热量大于因炉内烟气平均温度的降低而减少的辐射换热量，那么，炉膛出口烟温下降。如果α″_l过小，则炉膛出口烟温上升。上述分析是限制在燃料的燃烧处于正常工况，即α″_l的变化不致于造成燃料的不完全燃烧，否则情况将更加复杂。

过量空气系数的变化还会改变灰渣的物理特性，因为一些煤种的灰熔点与烟气的“气氛”有关，在氧化性气氛中灰熔点比在还原性气氛中低。当α″_l增加时，燃烧器附近烟气的氧化性气氛增强，灰熔点降低，燃烧器附近受热面结渣现象趋于严重，从而导致炉膛出口烟温的升高。

锅炉运行时，炉膛负压的变化，炉膛漏风量改变也会引起炉膛出口过量空气系数的变化。炉膛负压过大，炉壁漏风严重，α″_l增加。这些漏入炉膛中的冷空气对燃烧毫无帮助，只能降低炉膛的温度水平，削弱辐射传热过程，造成炉膛出口烟温的升高。所以，锅炉运行时应保持适当的炉膛负压，减少锅炉漏风。

⑦烟气再循环。部分烟气送入炉膛后可以改变炉膛烟气的平均热容量，降低炉膛烟气的平均温度，改变炉膛受热面的热负荷，控制炉膛出口烟温。再循环烟气送入炉膛的位置不同，再循环烟气量不同，对炉膛出口烟温的影响也不同。因此，烟气再循环工况的改变常用来作为调节锅炉蒸汽参数的手段。

（4）炉膛传热计算方法存在的问题及改进

计算表明，对于小容量锅炉，在（X_r＋ΔX）＝0～0.25范围内，（X_r＋ΔX）对θ″_l的影响较小，故在1957年标准中将M取为定值，即0.445。随着锅炉容量的增大，为考虑沿炉膛高度方向温度场的不均匀性对炉内换热的影响，1973年标准中将M写成燃料性质及燃烧器中心相对标高的函数形式，即M＝A－B（X_r＋ΔX）。

前苏联的研究表明，1973年标准中炉膛出口烟温计算式对于蒸发量小于（230～300）t/h的锅炉在理论燃烧温度T_ll＞（1900～2000）K的条件下，计算结果是准确的。当应用到较大容量锅炉（600～2650t/h）的炉膛换热计算时发现，实际的炉膛出口烟温T″_l比用1973年标准计算值高出（100～130）K；而对于采用风扇磨煤机的炉膛燃烧低质褐煤时，炉内过程因受烟气再循环的影响，炉膛出口烟温比73标准计算值低（50～80）K。炉膛出口烟温计算的准确性直接影响过热器工作的可靠性。

我国使用这一方法的经验表明，对于多数燃烧烟煤、贫煤的中、小容量电站锅炉，应用1973年标准得到的炉膛出口烟温的计算值是比较准确的。但对于某些高参数大容量锅炉或者燃用无烟煤、褐煤的锅炉，却不同程度地出现了一些问题。例如，对于燃烧褐煤的锅炉，特别是用热炉烟干燥燃料时，实际炉膛出口烟温比计算值低。相反，对于燃用无烟煤的锅炉，实测值常常高于计算值。多数高压以上锅炉（特别是燃油锅炉）普遍存在有过热蒸汽超温现象。这与原苏联所发现的问题是完全一致的。

造成偏差的原因除了传热模型本身存在的缺陷外，未能正确考虑炉内温度场、炉膛几何形状等对炉内传热的影响也是重要因素。

为了考虑炉内温度场不均匀性对炉膛传热的影响，原苏联标准把火焰有效平均温度T_yx作为独立参数引入到了计算式中。综合考虑了不同容量锅炉机组燃用不同种类燃料时炉内总换热量和温度场试验数据后，提出了如下的炉膛传热计算公式：

式中：T₀为炉膛假想温度。根据试验，当炉膛火焰有效平均温度T_yx＝T₀＝1470K时，按前述炉膛传热计算方法算出的炉膛吸热量与实际值吻合。如T_yx＞1470K，则计算值大于实际值；如T_yx＜1470K，则计算值小于实际值。在式（9.137）中，建议T₀＝1470K。

由1973年标准炉内换热计算准则方程式可得

将式（9.137）写成与1973年标准相似的形式，并注意Θ″_l＝，则有

该关系式中附加考虑了温度函数

对炉内换热的影响。

若取T₀＝1470K，则式（9.140）可写成

该法提高炉内总换热计算准确度是在计算关系式中更完全地考虑炉膛容积、温度场的性质对换热的影响，沿炉膛高度方向影响因子为M，炉膛横截面内为M′，即

由此可见，在改进的炉膛传热计算方法中是用来代表火焰有效平均温度T_yx，而用T_yx/T₀来反映炉膛温度场不均匀性对炉膛传热的影响。大量试验结果表明，在容量为160～2650t/h的各种锅炉中，采用改进的炉膛传热计算公式（9.141）得到的炉膛出口烟气温度与实测值相比，大多数试验点的偏差均不超过±30℃，也即都处在试验数据本身的精度范围以内。