试验布置及结果分析

6.4　试验布置及结果分析

6.4.1　试验布置

具体布置如下：

①试验在图4.1所示的变坡水槽内进行，试验段长度为2.0 m。调节15块固化卵石粗糙板，使其比降达到试验要求，粗糙板顶部高程误差不超过0.5 mm。

②试验粗颗粒泥沙的铺制，如图6.3～图6.6所示。首先将试验泥沙倒入2.0 m×1.0 m×0.25 m的试验段内，用2 m长的铝合金尺平整，其泥沙颗粒的顶部高度与上下粗糙板在同一坡度，纵向和横向的顶部高差不超过0.5 mm。

图6.3　泥沙起动布置示意图

图6.4　起动泥沙粒径

图6.5　起动试验布置

图6.6　起动试验过程

6.4.2　试验内容

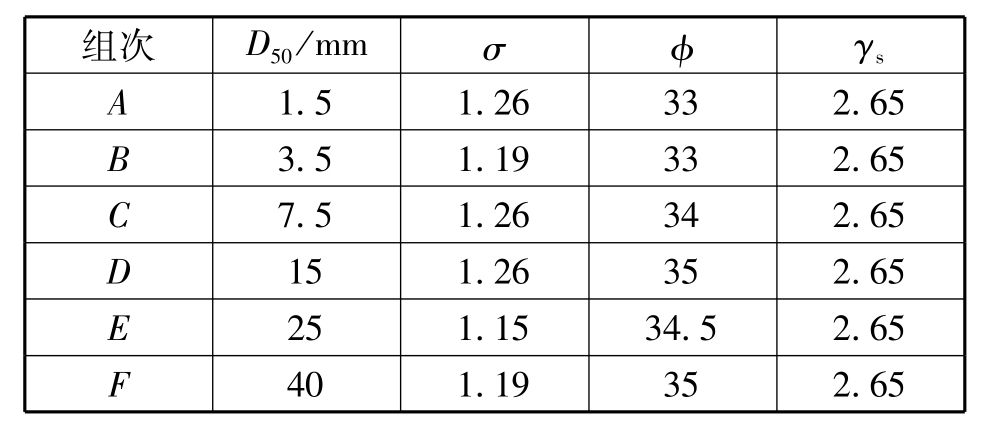
试验泥沙特性见表6.2。非均匀系数σ表示泥沙组成的均匀程度，其确定方法有2种，即：

不同学者对于非均匀沙和均匀沙的临界值的确定有不同看法，现在比较公认的是：以式（6.23）表达的公式，Yang（2002年）认为临界值σ＝2. 0^[109]；以式（6.23）表达的公式，Dey（1995年）认为临界值σ＝1.4^[109]。本文采用式（6.25）的表示方式，当σ≤1.4为均匀沙，当σ＞1.4为非均匀沙。

本试验的泥沙粒径范围为1.5～40 mm，非均匀系数为1.15～1.26，比降范围为0.5%～2.5%，流量范围为3～300 L/s。其泥沙起动按上节提出的标准。

表6.2　泥沙特性

6.4.3　试验步骤

每组起动试验数据的确定，采用如下步骤：

①初步确定试验流量。在试验段铺好砂样，逐渐增加流量，直到泥沙有少量起动。观测单宽输沙率和水力参数（比降、水深、流速和温度）。选择出粗颗粒泥沙起动标准相近的试验流量为初步确定流量Q₁。

②再次确定试验流量。重新铺砂样，逐渐增加流量到Q₁和[1＋（3～10）%] Q₁。选择出与粗颗粒泥沙起动标准相近的试验流量为再次确定流量Q₂。

③精确确定试验流量。重新铺砂样，逐渐增加流量到Q₂，观测单宽输沙率和水力参数（比降、水深、流速和温度），如与粗颗粒泥沙起动标准相近，则采用相应的水力参数为该组比降和粒径的泥沙起动数据，如不符合，重复第②步。

水槽试验数据共进行了21组，每组数据的确定至少经过以上3个步骤，由于泥沙运动的随机性，最长达到6步。具体试验情况见表6.3。

6.4.4　分析方法

分析流速起动试验成果，采取如下步骤：

①确定式（6.23）中的F（β）。只要比降已知，表6.2给出了泥沙的休止角φ，按式（6.19）可计算出F（β）。

②根据试验数据，采取多种方法拟合无量纲拖曳力与弗劳德数的关系。

6.4.5　成果处理

将21组数据按照上述方法进行整理，整理的结果见表6.3和图6.7。

表6.3　均匀粗颗粒泥沙起动水力参数及结果

流速起动的资料拟合出起动拖曳力公式为：

0.005＜J＜0.025；2＜H/D＜9；0.7＜Fr＜1.6。

相关系数R²＝0.90，表6.3列出计算与实测无量纲拖曳力，其相差值较小。

当比降为J＝0.005～0.025时，F（β）变化为F（β）＝0.924～0.948，对F（β）取平均值，则起动拖曳力公式为：

0.005＜J＜0.025；2＜H/D＜9；0.7＜Fr＜1.6。

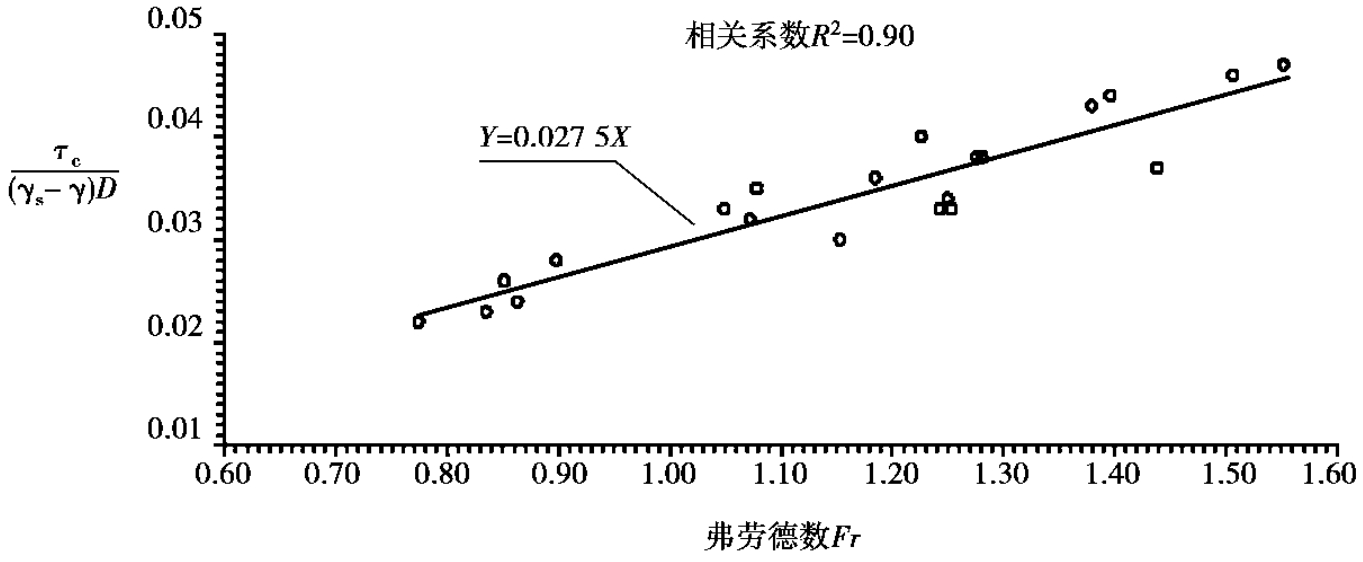
图6.7　大比降粗颗粒泥沙起动条件（无量纲拖曳力表示）

6.4.6　与Maxwell的成果比较

第1章已经提到Maxwell（2000年）在研究大比降山区河流泥沙起动时，泥沙起动的拖曳力无量纲数决定于弗劳德数Fr，其公式为

该公式的试验范围，河床比降：0.03＜J＜0.07；相对光滑度：0.5＜H/D₈₄＜2.5；弗劳德数：0.8＜Fr＜1.3；粒径范围：30 mm＜D₈₄＜110 mm。

大比降粗颗粒的泥沙起动公式与Maxwell的公式相比，有其相同点和不同点。

①相同点：起动拖曳力无量纲数都直接与弗劳德数相关，说明弗劳德数是大比降粗颗粒泥沙起动的重要参数。

②不同点：Maxwell在考虑粗颗粒泥沙起动的主要对象是台阶状的山区河流，如图6.8所示，中小卵石的起动受到处于台阶处的大卵石的影响，同时中小卵石的河床局部比降比较平缓，并没有“感受”到河床坡度自重分力的影响，因而难于起动。内流河宽浅变迁河段的河床上的卵砾石坡度基本上均匀的（具体见第3章），不管是卵石还是砾石都受到自重分力的影响。所以尽管本次试验的坡度比Maxwell的试验河床坡度小，但大比降粗颗粒起动的无量纲数反而小。

图6.8　与Maxwell研究对象的区别

（a）台阶状山区河流；（b）内流河宽浅变迁河流