网络计划优化概述

4　网络计划技术

本章提要：本章介绍了双代号网络图和单代号网络图的绘制方法和时间参数的计算，并结合例题对双代号网络计划进行优化和调整。

4．1　概述

用网络分析的方法编制的计划称为网络计划，它是20世纪50年代末发展起来的一种编制大型工程进度计划的有效方法。

1956年，美国杜邦公司在制定企业不同业务部门的系统规划时，制定了第一套网络计划。这种计划借助于网络表示各项工作与所需要的时间，以及各项工作之间的相互关系。通过网络分析研究工程费用与工期的相互关系，并找出在编制计划时及计划执行过程中的关键路线。这种方法称为关键路线法（Critical Path Method，简称CPM）。

1958年，美国海军武器部在制定“北极星”导弹计划时应用了网络分析方法与网络计划。但它注重于对各项工作安排的评价和审查。这种计划称为计划评审方法（Program E－valuation and Review Technique，简称PERT）。

两种方法的差别在于，CPM主要应用于以往在类似工程中已取得一定经验的承包工程；PERT更多地应用于研究与开发项目。在这两种方法得到应用推广之后，又陆续出现了类似的最低成本和估算计划法、产品分析控制法、人员分配法、物资分配和多种项目计划制定法等。虽然方法很多，各自侧重的目标有所不同，但它们都应用的是CPM和PERT的基本原理和基本方法。

20世纪60年代我国开始应用CPM与PERT，并根据其基本原理与计划的表达形式，称它们为网络技术或网络方法，又按照其主要特点——统筹安排，把这些方法称为统筹法。

国内外应用网络计划的实践表明，它具有一系列优点，特别适用于生产技术复杂、工作项目繁多且联系紧密的一些跨部门的工作计划。例如新产品研制开发、大型工程项目、生产技术准备、设备大修等计划。还可以应用于人力、物力、财力等资源的安排，合理组织报表、文件流程等方面。

以下主要介绍CPM，关于PERT可参阅相关教材。编制网络计划包括绘制网络图、计算时间参数、确定关键路线及网络优化等环节。下面分别讨论这些内容。

4．1．1　网络计划的基本原理

（1）利用网络图的形式表达一项工程中各项工作的先后顺序及逻辑关系。

（2）通过对网络图时间参数的计算，找出关键工作、关键线路。

（3）利用优化原理，改善网络计划的初始方案，以选择最优方案。

（4）在网络计划的执行过程中进行有效的控制和监督，保证合理地利用资源，力求以最少的消耗获取最佳的经济效益和社会效益。

4．1．2　横道图与网路图的比较

建筑工程施工进度计划是通过施工进度图表来表达建筑产品的施工过程、工艺顺序和相互间搭接逻辑关系的。我国长期以来一直应用流水施工基本原理，采用横道图的形式来编制工程项目施工进度计划。这种表达方式简单明了、直观易懂、容易掌握，便于检查和计算资源需求状况。但它在表现内容上有许多不足，例如不能全面而准确地反映出各工作之间相互制约、相互依赖、相互影响的关系；不能反映出整个计划中的主次部分，即其中的关键工作；难以在有限的资源下合理组织施工、挖掘计划的潜力；不能准确评价计划经济指标；更重要的是不能应用现代计算机技术。这些不足从根本上限制了横道图进度计划的适应范围。

与横道图相比，网络图克服了许多缺点，但也有其缺点。下面我们来总结网络图的优缺点。

优点：

（1）能全面而明确地反映出各项工作之间开展的先后顺序以及它们之间相互制约、相互依赖的关系。

（2）可以进行各种时间参数的计算。

（3）能在工作繁多、错综复杂的计划中找出影响工程进度的关键工作和关键线路，便于管理者抓住主要矛盾，集中精力确保工期，避免盲目施工。

（4）能够从许多可行方案中选出最优方案。

（5）保证自始至终对计划进行有效的控制与监督。

（6）利用网络计划中反映出的各项工作的时间储备，可以更好地调配人力、物力，以达到降低成本的目的。

（7）可以利用计算机进行计算、优化、调整和管理。

缺点：在计算劳动力、资源消耗量时，与横道图相比较为困难。

基于网络图有以上实用的优点，所以网络图能够得到广泛的应用。

4．1．3　网络计划技术的分类

1）按逻辑关系及工作持续时间是否确定划分

按各项工作持续时间和各项工作之间的相互关系是否确定，网络计划可分为肯定型和非肯定型两类。肯定型网络计划的类型主要有：关键线路法（CPM）、搭接网络计划、有时限的网络计划、多级网络计划和流水网络计划。非肯定型网络计划的类型主要有：计划评审技术（PERT）、图形评审技术（GERT）、风险评审技术（VERT）、决策网络计划法（DN）、随机网络计划技术（QERT）和仿真网络计划技术等。

2）按工作的表示方式不同划分

按工作的表示方式不同，网络计划可分为双代号网络计划（如图4－1）、单代号网络计划（如图4－2）、时标网络计划（如图4－3）。

图4－1　双代号网络计划

图4－2　单代号网络计划

图4－3　时标网络计划

3）按目标的多少划分

按目标的多少，网络计划可分为单目标网络计划和多目标网络计划。

4）按其发展过程划分

按其发展过程，网络计划可分为关键线路（CPM）、计划评审技术（PERT）、图示评审技术（GERT）、风险评审技术（VERT）、决策网络计划（DN）和随机网络计划技术（QERT）。

5）按其应用对象不同划分

按其应用对象的不同，分为分部工程网络计划、单位工程网络计划和群体工程网络计划。

4．2　双代号网络图

目前在我国的工程施工中，经常用以表示工程进度计划的网络图是双代号网络图。这种网络图是由若干表示工作的箭线和节点所组成的，其中每一项工作都用一根箭线和两个节点来表示，每个节点都编以号码，箭线前后两个节点的号码即代表该箭线所表示的工作，“双代号”的名称即由此而来。图4－4表示的就是双代号网络图。下面就图中3个基本符号的有关含义和特性作一介绍。

图4－4　带虚拟节点的双代号网络图

4．2．1　基本要素

1）箭线（工作）

（1）在双代号网络图中，每一条箭线表示一项工作。箭线的箭尾节点表示该工作的开始，箭头节点表示该工作的结束。工作的名称标注在箭线的上方，完成该项工作所需要的持续时间标注在箭线的下方，如图4－5所示。由于一项工作需用一条箭线及其箭尾和箭头处两个圆圈中的号码来表示，因此称为双代号表示法。

图4－5　双代号网络图工作的表示方法

图4－6　双代号网络图中虚箭线表示的虚拟工作

（2）在双代号网络图中，任意一条实箭线都要占用时间、消耗资源（有时只占时间，不消耗资源，如混凝土的养护）。在建筑工程中，一条箭线表示项目中的一个施工过程，它可以是一道工序、一个分项工程、一个分部工程或一个单位工程，其粗细程度、大小范围的划分根据计划任务的需要来确定。

（3）在双代号网络图中，为了正确地表达图中工作之间的逻辑关系，往往需要应用虚箭线，其表示方法如图4－6所示。

虚箭线是实际工作中并不存在的一项虚拟工作，故它们既不占用时间，也不消耗资源，一般起着工作之间的联系、区分和断路3个作用。联系作用是指应用虚箭线正确表达工作之间相互依存的关系，如图4－7所示，把工作A和D、B和D联系起来了；区分作用是指双代号网络图中每一项工作都必须用一条箭线和两个代号表示，若两项工作的代号相同，应使用虚工作加以区分，如图4－7所示；断路作用是用虚箭线断掉多余联系（即在网络图中把无联系的工作连接上时，应加上虚工作将其断开），如图4－9（a）所示是一个逻辑关系错误的网络图，其中A为挖槽、B为垫层、C为墙基、D为回填土，利用虚箭线的断路作用把错误的网络图更正为图4－9（b）。

图4－7　虚箭线的联系作用

图4－8　虚箭线的区分作用

图4－9　虚箭线的断路作用

（4）在无时间坐标限制的网络图中，箭线的长度原则上可以任意画，其占用的时间以下方标注的时间参数为准。箭线可以为直线、折线或斜线，但其行进方向均应从左向右，如图4－10所示。在有时间坐标限制的网络图中，箭线的长度必须根据完成该工作所需持续时间的大小按比例绘制。

图4－10　箭线的表达形式

（5）在双代号网络图中，各项工作之间的关系如图4－9所示。通常将被研究的对象称为本工作，用i－j工作表示，紧排在本工作之前的工作称为紧前工作，紧排在本工作之后的工作称为紧后工作，与之平行进行的工作称为平行工作。例如，D1是C2的平行工作，C1是C2的紧前工作，D2是C2的紧后工作。

2）节点（又称结点、事件）

节点是网络图中箭线之间的连接点。在双代号网络图中，节点既不占用时间也不消耗资源，是个瞬时值，即它只表示工作的开始或结束的瞬间，起着承上启下的衔接作用。网络图中有3种类型的节点：

（1）起点节点

网络图的第一个节点叫“起点节点”，它只有外向箭线，一般表示一项任务或一个项目的开始，如图4－11所示。

（2）终点节点

网络图的最后一个节点叫“终点节点”，它只有内向箭线，一般表示一项任务或一个项目的完成，如图4－12所示。

（3）中间节点

网络图中既有内向箭线又有外向箭线的节点称为中间节点，如图4－13所示。

图4－11　起点节点

图4－12　终点节点

图4－13　中间节点

（4）在双代号网络图中，节点应用圆圈表示，并在圆圈内编号。一项工作应当只有唯一的一条箭线和相应的一对节点。如图4－14所示。

图4－14　节点和工作

3）线路

网络图中从起点节点开始，沿箭头方向顺序通过一系列箭线与节点，最后达到终点节点的通路称为线路。线路上各项工作持续时间的总和称为该线路的计算工期。一般网络图有多条线路，可依次用该线路上的节点代号来记述。例如网络图4－15中的线路有：①—②—④—⑥、①—②—③—④—⑥、①—②—③—④—⑤—⑥、①—③—④—⑤—⑥、①—③—⑤—⑥、①—③—④—⑥等，其中最长的一条线路称为关键线路，位于①—③—④—⑥，关键线路上的工作称为关键工作。

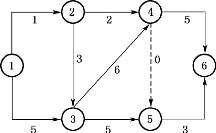
图4－15　线路和关键线路

4．2．2　逻辑关系

网络图中工作之间相互制约或相互依赖的关系称为逻辑关系，它包括工艺关系和组织关系，在网络中均应表现为工作之间的先后顺序。

1）工艺关系

生产性工作之间由工艺过程决定的、非生产性工作之间由工作程序决定的先后顺序叫工艺关系。例如，建筑工程施工时，先做基础，后做主体；先做结构，后做装修。工艺关系是不能随意改变的。如图4－16所示，挖基槽1－垫层1－混凝土基础1－墙基1－回填1为工艺关系。

2）组织关系

组织关系是指在不违反工艺关系的前提下，人为安排工作的先后顺序。例如，建筑群中各个建筑物的开工顺序的先后；施工对象的流水作业等。组织顺序可以根据具体情况，按安全、经济、高效的原则统筹安排。如图4－16所示，挖基槽1－挖基槽2；垫层1－垫层2等为组织关系。

图4－16　逻辑关系

网络图必须正确地表达整个工程或任务的工艺流程和各工作开展的先后顺序以及它们之间相互依赖、相互制约的逻辑关系。因此，绘制网络图时必须遵循一定的基本规则和要求。

4．2．3　绘图规则

绘制双代号网络图时，要正确地表示工作之间的逻辑关系和遵循有关绘图的基本规则。否则，就不能正确反映工程的工作流程和进行时间计算。绘制双代号网络图一般必须遵循以下一些基本规则。

（1）双代号网络图必须正确表达已定的逻辑关系。在表示工程施工计划的网络图中，根据施工工艺和施工组织的要求，应正确反映各项工作之间的相互依赖和相互制约的关系，这也是网络图与横道图的最大不同点。各工作间的逻辑关系是否表示得正确，是网络图能否反映工程实际情况的关键。如果逻辑关系错了，网络图中各种时间参数的计算就会发生错误，关键线路和工程的计算工期跟着也将发生错误。

要画出一个正确反映工程逻辑关系的网络图，首先就要搞清楚各项工作之间的逻辑关系，也就是要具体解决每项工作的下面3个问题：

①该工作必须在哪些工作之前进行？

②该工作必须在哪些工作之后进行？

③该工作可以与哪些工作平行进行？

图4－17中，就工作B而言，它必须在工作E之前进行，是工作E的紧前工作；工作B须在工作A之后进行，是工作A的紧后工作；工作B可以与工作C和D平行进行，是工作C和D的平行工作。这种严格的逻辑关系，必须根据施工工艺和施工组织的要求加以确定，只有这样才能逐步地按工作的先后次序把代表各工作的箭线连接起来，绘制成一张正确的网络图。

图4－17　工作的逻辑关系

在网络图中，各工作之间在逻辑上的关系是变化的。表4－1所列的是网络图中常见的一些逻辑关系及其表示方法，表中的工作名称均以字母来表示。

绘制网络图之前，要正确确定工作顺序，明确各工作之间的衔接关系，根据工作的先后顺序逐步把代表各项工作的箭线连接起来，绘制成网络图。

表4－1　双代号网络图中各工作逻辑关系表示方法

续表　4－1

（2）双代号网络图中，严禁出现循环网络（图4－18）。

在网络图中如果从一个节点出发顺着某一线路又能回到原出发点，这种线路就称为循环回路。例如图4－18中的2—4—5—3—2就是循环回路，它表示的逻辑关系是错误的，在工艺顺序上是相互矛盾的。

（3）双代号网络图中，在节点之间严禁出现带双向箭头或无箭头的连线。

用于表示工程计划的网络图是一种有序有向图，沿着箭头指引的方向进行，因此一条箭线只有一个箭头，不允许出现方向矛盾的双箭头箭线和无方向的无箭头箭线，如图4－19中的2—4和3—4。

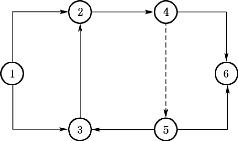
图4－18　不允许出现循环线路

图4－19　出现双向箭头箭线和无箭头箭线错误的网络图

（4）在双代号网络图中，严禁出现没有箭头节点或没有箭尾节点的箭线。图4－20中，图（a）出现了没有箭头节点的箭线，图（b）中出现了没有箭尾节点的箭线，都是不允许的。没有箭头节点的箭线，不能表示它所代表的工作在何处完成；没有箭尾节点的箭线，不能表示它所代表的工作在何时开始。

图4－20　没有箭头节点的箭线和没有箭尾节点的箭线的错误网络图

（5）当双代号网络图的某些节点有多条内向箭线或多条外向箭线时，在不违反“一项工作应只有唯一的一条箭线和相应的一对节点编号”的规定的前提下，可使用母线法绘图。当箭线线型不同时，可在母线上引出的支线上标出。图4－21是母线的表示方法。

图4－21　母线的表示方法

（6）绘制网络图时，箭线不宜交叉。当交叉不可避免时，可用过桥法或指向法。图4－22中，图（a）为过桥法，图（b）为指向法。

图4－22　过桥法交叉与指向法交叉

（7）双代号网络图中应只有一个起点节点；在不分期完成任务的网络图中，应只有一个终点节点；而其他所有节点均应是中间节点。图4－23（a）所示的网络图中①、④节点均没有内向箭线，故可认为两个节点都是起点节点，这是不允许的。如果遇到这种情况，最简单的办法就是像图4－23（b）那样，用虚箭线把①、④节点连接起来，使之变成一个起点节点。在本例中，如果把④节点删除，也可以直接把①、⑤两节点用箭线连接起来。

图4－23　只允许有一个起点节点

在图4－24（a）中，出现了两个没有外向箭线的节点④、⑦，可认为是有两个终点节点。如果没有分批完成任务的要求，这也是不允许的。解决办法是像图4－24（b）那样，使它变成一个终点节点。在本例中，最好是去掉多余的④节点，而直接把②、⑦节点连接起来，形成一个终点节点⑦。

图4－24　只允许有一个终点节点

4．2．4　网络图的编号

按照各项工作的逻辑顺序将网络图绘好之后，即可进行节点编号。节点编号的目的是赋予每项工作一个代号，并便于对网络图进行时间参数的计算。当采用计算机进行计算时，工作代号就是绝对必要的。

1）网络图的节点编号应遵循两条规则

（1）一条箭线（工作）的箭头节点的编号“j”，一般应大于箭尾节点“i”，即i＜j，编号时号码应当从小到大，箭头节点编号必须在其前面的所有箭尾节点都已编号之后进行。如图4－25中，为给节点③编号，就必须先给节点①、②编号。如果在节点①编号后就给节点③编号为②，那么原来节点②就只能编为③（如图4－25（b）所示）。这样就会出现③→②，即i＞j，以后在进行计算时就很容易出现错误。

图4－25　节点编号时应箭头节点大于箭尾节点

（2）在一个网络计划中，所有的节点不能出现重复编号。有时考虑到可能在网络图中会增添或改动某些工作，故在节点编号时，可预先留出备用的节点号，即采用不连续编号的方法，如1，3，5……或1，5，10……以便于调整，避免以后由于中间增加一项或几项工作而改动整个网络图的节点编号。

2）网络图节点编号的方法

网络图的节点编号除应遵循上述原则外，在编排方法上也有技巧，一般编号方法有两种，即水平编号法和垂直编号法。

（1）水平编号法

水平编号法就是从起点节点开始由上到下逐行编号，每行则自左到右按顺序编排，如图4－26所示。

图4－26　水平编号法

图4－27　垂直编号法

（2）垂直编号法

垂直编号法就是从起点节点开始自左到右逐列编号，每列则根据编号规则的要求或自上而下，或自下而上，或先上下后中间，或先中间后上下，如图4－27所示。

4．2．5　双代号网络图的绘制方法

网络计划是用来指导实际工作的，所以网络图除了要符合逻辑外，图面还必须清晰，要进行周密合理的布置。

在正式绘制网络图之前，最好先绘成草图，然后再加以整理，就显得条理清楚，布局也比较合理了。

在此，我们采用逻辑草稿法进行双代号网络图的绘制，当已知每一项工作的紧前工作时，可按下述步骤绘制双代号网络图。

（1）绘制没有紧前工作的工作，使它们具有相同的箭尾节点，即起点节点。

（2）依次绘制其他各项工作。这些工作的绘制条件是将其所有紧前工作都已经绘制出来。绘制原则为：

①当所绘制的工作只有一个紧前工作时，则将该工作的箭线直接画在其紧前工作的完成节点之后即可。

②当所绘制的工作有多个紧前工作时，应按以下4种情况分别考虑：

A．如果在其紧前工作中只存在一项作为本工作紧前工作的工作（即在紧前工作栏目中，该紧前工作只出现一次），则应将本工作箭线直接画在该紧前工作完成节点之后，然后用虚箭线分别将其他紧前工作的完成节点与本工作的开始节点相连，以表达它们之间的逻辑关系。

B．如果在其紧前工作中存在多项作为本工作紧前工作的工作，应将这些紧前工作的完成节点合并（利用虚工作或直接合并），再从合并后的节点开始，画出本工作箭线，最后用虚箭线将其他紧前工作的箭头节点分别与工作开始节点相连，以表达它们之间的逻辑关系。

C．如果不存在情况A、B，应判断本工作的所有紧前工作是否都同时作为其他工作的紧前工作（即紧前工作栏目中，这几项紧前工作是否均同时出现若干次）。如果是这样，应先将它们完成节点合并后，再从合并的节点开始画出本工作箭线。

D．如果不存在情况A、B、C，则应将本工作箭线单独画在其紧前工作箭线之后的中部，然后用虚工作将紧前工作与本工作相连，表达它们之间的逻辑关系。

③合并没有紧后工作的箭线，即为终点节点。

④确认无误，进行节点编号。

【例4－1】　根据下表中各工作的逻辑关系，绘制双代号网络图。

【解】　（1）绘没有紧前工作的工作A、B，且它们的起点节点为①，它们的箭尾节点分别为②、③。

（2）由于工作C、D、E的紧前工作都已确定且绘制完成，所以接下来绘制工作C、D、E，且画出工作C、D、E的箭尾节点⑤、④、⑥。

（3）此时，只剩下工作G、F没有布置，且其紧前工作已经确定，而且E、F、G是没有紧后工作的工作，即它们有共同终点节点。

（4）最后把不相关的工作B、C和C、G用虚箭线断开，且合理地布置网络图，做到符合逻辑，画面清晰。绘制结果如图4－28。

图4－28　双代号网络图绘图结果

【例4－2】　已知各项工作之间的逻辑关系如下表所示，试绘制双代号网络图。

【解】　绘制过程如图4－29。

图4－29　双代号网络图绘图过程

上面两例是比较简单的例子，但实际工程是个复杂的过程。当然，其用双代号网络图表示的逻辑关系也是比较复杂的，下面是我们总结出来的对于复杂网络图绘制的注意事项。

（1）网络图布局要条理清楚、突出重点。虽然网络图主要用以表达各工作之间的逻辑关系，但为了使用方便，布局应层次分明、行列有序，同时还应突出重点，尽量把关键工作和关键线路布置在中心位置。

（2）正确应用虚箭线进行网络图的断路。应用虚箭线进行网络图断路，是正确表达工作之间逻辑关系的关键。

（3）力求减少不必要的箭线和节点。双代号网络图中，应在满足绘图规则和两个节点一根箭线代表一项工作的原则基础上，力求减少不必要的箭线和节点，使网络图图面简洁，减少时间参数的计算值。

（4）网络图的分解。当网络图中的工作任务较多时，可以把它分成几个小块来绘制。分界点一般选择在箭线和节点较少的地方，或按施工部位分块。分解点要用重复编号，即前一块最后一节点的编号与后一块的第一个节点的编号相同。

4．2．6　双代号网络计划时间参数的计算

双代号网络计划时间参数计算的目的在于通过计算各项工作的时间参数，确定网络计划的关键工作、关键线路和计算工期，为网络计划的优化、调整和执行提供明确的时间参数。双代号网络计划时间参数的计算方法很多，一般常用的有按工作计算法和按节点计算法进行计算；在计算方式上又有分析计算法、表上计算法、图上计算法、矩阵计算法和电算法等。本节只介绍按工作计算法在图上进行计算的方法（图上计算法）。

1）时间参数的概念及其符号

（1）工作持续时间（Di－j）

工作持续时间是对一项工作规定的从开始到完成的时间。在双代号网络计划中，工作i－j的持续时间用Di－j表示。

（2）工期（T）

工期泛指完成任务所需要的时间，一般有以下3种：

①计算工期。根据网络计划时间参数计算出来的工期，用TC表示。

②要求工期。任务委托人所要求的工期，用TR表示。

③计划工期。在要求工期和计算工期的基础上综合考虑需要和可能而确定的工期，用TP表示。网络计划的计划工期TP应按下列情况分别确定：

A．当已规定了要求工期TR时：

B．当未规定要求工期时，可令计划工期等于计算工期：

（3）网络计划中工作的6个时间参数

①最早开始时间和最早完成时间是指在各紧前工作全部完成后，本工作有可能开始的最早时刻。工作i－j的最早开始时间用表示。是指在各紧前工作全部完成后，本工作有可能完成的最早时刻。工作i－j的最早完成时间用表示。

这类时间参数的实质是提出了紧后工作与紧前工作的关系，紧后工作若提前开始，也不能提前到其紧前工作未完成之前。就整个网络图而言，受到起点节点的控制。因此，其计算程序为：自起点节点开始，顺着箭线方向，用累加的方法计算到终点节点。

②最迟完成时间和最迟开始时间是指在不影响整个任务按期完成的前提下，工作必须完成的最迟时刻。工作i－j的最迟完成时间用表示。是指在不影响整个任务按期完成的前提下，工作必须开始的最迟时刻。工作i－j的最迟开始时间用表示。

这类时间参数的实质是提出了紧前工作与紧后工作的关系，即紧前工作要推迟开始，不能影响其紧后工作的按期完成。就整个网络图而言，受到终点节点（即计算工期）的控制。因此，其计算程序为：自终点节点开始，逆着箭线方向，用累减的方法计算到起点节点。

③总时差和自由时差是指在不影响总工期的前提下，本工作可以利用的机动时间。工作i－j的总时差用表示。是指在不影响其紧后工作最早开始的前提下，本工作可以利用的机动时间。工作i－j的自由时差用表示。

（4）网络计划中节点的时间参数及其计算程序

①节点最早时间

双代号网络计划中，以该节点为开始节点的各项工作的最早开始时间，称为节点最早时间。节点i的最早时间用ETi表示。计算程序为：自起点节点开始，顺着箭线方向，用累加的方法计算到终点节点。

②节点最迟时间

双代号网络计划中，以该节点为完成节点的各项工作的最迟完成时间，称为节点最迟时间。节点i的最迟时间用LTi表示。计算程序为：自终点节点开始，逆着箭线方向，用累减的方法计算到起点节点。

2）双代号网络计划时间参数的计算

双代号网络计划时间参数的计算方法通常有工作计算法、节点计算法、图上计算法和表上计算法。这里我们仅学习前3种方法。

（1）工作计算法

按工作计算法计算时间参数应在确立了各项工作的持续时间之后进行。虚工作也必须视同工作进行计算，其持续时间为零。时间参数的计算结果应标注在箭线之上，如图4－30所示。

下面以双代号网络计划（图4－31）为例，说明其计算步骤。

图4－30　双代号网络计划计算实例

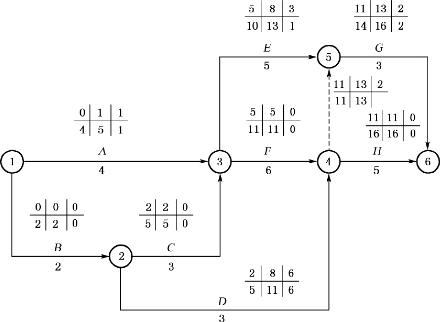
图4－31　双代号网络计划计算实例

①计算各项工作的最早开始时间和最早完成时间

各项工作的最早完成时间等于其最早开始时间加上工作持续时间，即

计算工作最早时间参数时，一般有以下3种情况：

A．以工作起点节点为开始节点时，其最早开始时间为零（或规定时间），即：

B．当工作只有一项紧前工作时，该工作的最早开始时间应为其紧前工作的最早完成时间，即

C．当工作有多个紧前工作时，该工作的最早开始时间应为其所有紧前工作最早完成时间的最大值，即

如图4－31所示的网络计划中，各工作的最早开始时间和最早完成时间计算如下：

将以上计算结果标注在图中的相应位置。

上述计算可以看出，工作的最早时间计算时应特别注意以下3点：一是计算程序，即从起点节点开始顺着箭线方向，按节点次序逐项工作计算；二是弄清楚该工作的紧前工作是哪几项，以便准确计算；三是同一节点的所有外向工作最早开始时间相同。

②确定计算工期TC及计划工期TP

计算工期：

已知计划工期等于计算工期，即计划工期：

③计算各项工作的最迟开始时间和最迟完成时间

从终点节点（⑥节点）开始逆着箭线方向依次逐项计算到起点节点（①节点）。

各工作的最迟开始时间等于其最迟完成时间减去工作持续时间，即

计算工作最迟完成时间参数时，一般有以下3种情况：

A．当工作的终点节点为完成节点时，其最迟完成时间为网络计划的计划工期，即

B．当工作只有一项紧后工作时，该工作的最迟完成时间应为其紧后工作的最迟开始时间，即

C．当工作有多项紧后工作时，该工作的最迟完成时间应为其多项紧后工作最迟开始时间的最小值，即

如图4－31所示的网络计划中，各工作的最迟完成时间和最迟开始时间计算如下：

从上述计算中可以看出，工作的最迟时间计算时应特别注意以下3点：一是计算程序，即从终点节点开始逆着箭线方向，按节点次序逐项工作计算；二是要弄清楚该工作紧后工作有哪几项，以便正确计算；三是同一节点的所有内向工作最迟完成时间相同。

④计算各项工作的总时差 :

如图4－32所示，在不影响总工期的前提下，一项工作可以利用的时间范围是从该工作最早开始时间到最迟完成时间，即工作从最早开始时间开始或从最迟开始时间开始，均不会影响总工期。而工作实际需要的持续时间是扣去后，余下的一段时间就是工作可以利用的机动时间，即为总时差，所以总时差等于最迟开始时间减去最早开始时间，或最迟完成时间减去最早完成时间，即

图4－32　总时差计算简图

如图4－31所示的网络图中，各工作的总时差计算如下：

将以上计算结果标注在图中的相应位置。

通过计算表不难看出总时差有如下特性：

A．凡是总时差为最小的工作就是关键工作；由关键工作连接构成的线路为关键线路；关键线路上各工作时间总和就是总工期。如图4－31所示，工作1—2、2—3、3—4、4—6为关键工作，线路1—2—3—4—6为关键线路。

B．当网络计划的计划工期等于计算工期时，凡总时差大于零的工作为非关键工作，凡是具有非关键工作的线路就是非关键线路。非关键线路与关键线路相交时的相关节点把非关键线路划分成若干个非关键线路段，各段有各段的总时差，相互没有关系。

C．总时差的使用具有双重性，它既可以被该工作使用，但又属于某非关键线路。当某项工作使用了全部或部分总时差时，则将引起通过该工作的线路上所有工作总时差重新分配。例如图4－31中，非关键线路段3—5—6中，TF3—5＝3天，TF5—6＝2天，如果工作3—5使用了3天机动时间，则工作5—6就没有总时差可以利用了；反之，若工作5—6使用了2天机动时间，则工作3—5就只剩1天总时差可以利用了。

⑤计算各项工作的自由时差

如图4－33所示，在不影响其紧后工作的最早开始时间的前提下，一项工作可以利用的时间范围是从该工作最早开始时间至紧后工作最早开始时间。而工作实际需要的持续时间是扣去后，尚有的一段时间就是自由时差。所以自由时差等于紧后工作的最早开始时间减去本工作最早完成时间，即

图4－33　自由时差计算简图

如图4－31所示的网络图中，各工作的自由时差计算如下：

将以上计算结果标注在图中的相应位置。

通过计算不难看出，自由时差有以下特性：

A．自由时差为某非关键工作独立使用的机动时间，利用自由时差，不会影响其紧后工作的最早开始时间。例如图4－31中，工作3—5有1天自由时差，如果使用了1天机动时间，也不会影响其紧后工作5—6的最早开始时间。

B．非关键工作的自由时差必小于或等于其总时差。

（2）节点计算法

按节点计算法计算时间参数，其计算结果应标注在节点之上，如图4－34所示。

图4－34　节点时间参数标注形式

下面以图4－35为例，说明其计算步骤。

图4－35　双代号网络计划计算实例

①节点最早时间的计算

节点最早时间是指双代号网络计划中，以该节点为开始节点的各项工作的最早开始时间。

节点i的最早时间ETi应从网络计划的起点节点开始，顺着箭线方向，依次逐项计算，并应符合下列规定：

A．起点节点i如未规定最早时间ETi时，其值应等于零，即

B．当节点j只有一条内向箭线时，其最早时间

C．当节点j有多条内向箭线时，其最早时间ETj应为

如图4－35所示的网络计划中，各节点的最早时间计算如下：

算出全部节点的最早时间，见图4－35相应的标注。

②节点最迟时间的计算

节点最迟时间指双代号网络计划中，以该节点为完成节点的各项工作的最迟完成时间。节点i的最迟时间LTi应从网络计划的终点节点开始，逆着箭线方向依次逐项计算，并应符合下列规定：

A．节点i的最迟时间LTi应从网络计划的终点节点开始，逆着箭线方向依次逐项计算，当部分工作分期完成时，有关节点的最迟时间必须从分期完成节点开始逆向逐项计算。

B．终点节点n的最迟时间LTn，应按网络计划的计划工期TP确定，即

分期完成节点的最迟时间应等于该节点规定的分期完成时间。

C．其他节点i的最迟时间LTi，应为

式中：LTj——工作i－j的箭头节点j的最迟时间。

如图4－35所示的网络计划中，各节点的最迟时间计算如下：

③工作时间参数的计算

A．工作最早开始时间的计算

工作i－j的最早开始时间按下式计算：

按上式计算，图4－35的各项工作的最早开始时间计算如下：

B．工作i－j的最早完成时间的计算

工作i－j的最早完成时间按下式计算：

按上式计算，图4－35中各项工作的最早完成时间计算如下：

C．工作i－j的最迟完成时间LFi－j的计算

工作i－j的最早完成时间按下式计算：

按上式计算，图4－35中各项工作的最早完成时间计算如下：

D．工作i－j的最迟开始时间LSi－j的计算

工作i－j的最迟开始时间按下式计算：

按上式计算，图4－35中各项工作的最早完成时间计算如下：

E．工作i－j总时差TFi－j的计算

工作i－j的自由时差按下式计算：

按上式计算，图4－35中各项工作的总时差计算如下：

F．工作i－j自由时差FFi－j的计算

工作i－j的自由时差按下式计算：

按上式计算，图4－35中各项工作的自由时差计算如下：

（3）图上计算法

图上计算法是根据工作计算法或节点计算法的时间参数计算公式，在图上直接计算的一种比较直观、简便的方法。

①计算工作的最早开始时间和最早完成时间

以起点节点为开始节点的工作，其最早开始时间一般记为0，如图4－35所示的工作1—2和工作1—3。

其余工作的最早开始时间可采用“沿线累加，逢圈取大”的计算方法求得。即从网络图的起点节点开始，沿着每一条线路将各工作的作业时间累加起来，在每一个圆圈（节点）处，取到达该圆圈的各条线路累计时间的最大值，就是该节点为开始节点的各工作的最早开始时间。

工作的最早完成时间等于该工作的最早开始时间与本工作持续时间之和。

将计算结果标注在箭线上方各工作图例对应的位置上（图4－36）。

②计算工作的最迟开始时间和最迟完成时间

以终点节点为完成节点的工作，其最迟完成时间就是计划工期，如图4－35所示的工作4—6和工作5—6。

其余工作的最迟完成时间可采用“逆线累减，逢圈取小”的计算方法求得。即从网络图的终点节点逆着每条线路将计划工期依次减去各工作的持续时间，在每一个圆圈处取后续线路累减时间的最小值，就是以该节点为完成节点的各工作的最迟完成时间。

工作的最迟开始时间等于该工作最迟完成时间与本工作持续时间之差。

将计算结果标注在箭线上方各工作图例对应的位置上（图4－37）。

③计算工作的总时差

工作的总时差可采用“迟早相减，所得之差”的计算方法求得。即工作的总时差等于该工作的最迟开始时间减去工作的最早开始时间，或者等于该工作的最迟完成时间减去工作的最早完成时间。

将计算结果标注在箭线上方各工作图例对应的位置上（图4－38）。

④计算工作的自由时差

工作的自由时差等于紧后工作的最早开始时间减去本工作的最早完成时间。可在图上相应位置直接相减得到，并将计算结果标注在箭线上方各工作图例对应的位置上（图4－39）。

⑤计算节点最早时间

起点节点的最早时间一般记为0，如图4－40所示的①节点。其余节点的最早时间也可采用“沿线累加，逢圈取大”的计算方法求得。将计算结果标注在箭线上方各工作图例对应的位置上（图4－40）。

⑥计算节点最迟时间

终点节点的最迟时间等于计划工期。当网络计划有规定工期时，其最迟时间就等于规定工期；当没有规定工期时，其最迟时间就等于终点节点的最早时间。其余节点的最迟时间也可采用“逆线累减，逢圈取小”的计算方法求得。将计算结果标注在相应节点图例对应的位置上（图4－40）。

各参数计算结果见以下过程图。

图4－36　计算工作的最早开始和最早结束时间

图4－37　计算工作的最迟开始和最迟结束时间

图4－38　计算工作的总时差

图4－39　计算工作的自由时差

图4－40　计算节点的最早和最迟时间

3）网络计划工期的计算

（1）网络计划的计算工期

网络计划的计算工期按下式计算：

式中：ETn——终点节点n的最早时间。

因此，上例中的计算工期为

（2）网络计划的计划工期的确定

网络计划的计划工期TP的确定与工作计算法相同。因此，上例中的计划工期为

4）双代号网络计划关键工作和关键线路的确定

（1）关键工作的确定

①关键工作的概念

关键工作是网络计划中总时差最小的工作。

当计划工期与计算工期相等时，这个“最小值”为0；

当计划工期大于计算工期时，这个“最小值”为正；

当计划工期小于计算工期时，这个“最小值”为负。

②关键工作的确定

根据上述关键工作的定义，上例的最小总时差为零，故关键工作为1—2，2—3，3—4，4—6。

（2）关键线路的确定

①关键线路的概念

关键线路是自始至终全部由关键工作组成的线路，或线路上总的工作持续时间最长的线路。

②关键线路的确定

将关键工作自左而右依次首尾相连而形成的线路就是关键线路。因此，上例中的关键线路是1→2→3→4→6。

③关键工作和关键线路的标注

关键工作和关键线路在网络图上应当用粗线或双线或彩色线标注其箭线，见图4－41。

图4－41　双代号网络图的关键线路和关键工作

4．3　单代号网络图

由一个节点表示一项工作，以箭线表示工作顺序的网络图称为单代号网络图。单代号网络图的逻辑关系容易表达，且不用虚箭线，便于检查和修改。但不易绘制成时标网络计划，使用不直观。

4．3．1　单代号网络图的绘制

1）构成与基本符号

（1）节点

节点是单代号网络图的主要符号，用圆圈或方框表示。一个节点代表一项工作或工序，因而它消耗时间和资源。节点所表示工作的名称、持续时间和编号一般都标注在圆圈或方框内，有时甚至将时间参数也注在节点内，如图4－42所示。

图4－42　单代号网络的节点表示

（2）箭线

箭线在单代号网络图中，仅表示工作之间的逻辑关系。它既不占用时间，也不消耗资源。单代号网络图中不用虚箭线。箭线的箭头表示工作的前进方向，箭尾节点表示的工作是箭头节点的紧前工作。

2）编号

每个节点都必须编号，作为该节点工作的代号。一项工作只能有唯一的一个节点和唯一的一个代号，严禁出现重号。编号要由小到大，即箭头节点的号码要大于箭尾节点的号码。

4．3．2　单代号网络图绘制规则

（1）正确表达逻辑关系，如表4－2。

（2）严禁出现循环回路。

（3）严禁出现无箭尾节点或无箭头节点的箭线。

（4）严禁出现双向箭头或无箭头的连线。

（5）绘制网络图时，箭线不宜交叉。当交叉不可避免时，可采用过桥法和指向法绘制。

（6）只能有一个起点节点和一个终点节点。当开始的工作或结束的工作不止一项时，应在两端设虚拟开始节点（S）或结束节点（F），以避免出现多个起点节点或多个终点节点，如图4－43。

表4－2　单代号网络图中各工作逻辑关系表示方法

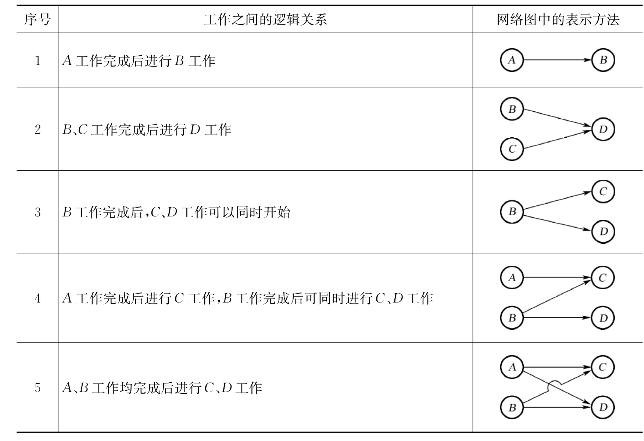
图4－43　带虚拟节点的单代号网络图

4．3．3　单代号网络图绘制方法

单代号网络图的绘制与双代号网络图的绘制方法基本相同，而且由于单代号网络图逻辑关系容易表达，因此绘制方法更为简便，其绘制步骤如下：

先根据网络图的逻辑关系绘制出网络图草图，再结合绘图规则进行局部调整，最后形成正式网络图。

（1）提供逻辑关系表，一般只需要提供每项工作的紧前工作。

（2）确定紧后工作。

（3）绘制没有紧后工作的工作，当网络图中有多项起点节点时，应在网络图的始端设置一项虚拟的起点节点。

（4）依次绘制出其他各项工作一直到终点节点。当网络图中有多项终点节点时，应在网络图的末端设置一项虚拟的终点节点。

【例4－3】　某工程分为3个施工段，施工过程及其延续时间为：砌围护墙及隔墙12天，内外抹灰15天，安铝合金门窗9天，喷刷涂料12天。拟组织瓦工、抹灰工、木工和油工4个专业队组进行施工。试绘制单代号网络图。

【解】　按照上述步骤，我们可以绘制出如图4－44所示的单代号网络图。

图4－44　单代号网络图

4．3．4　单代号网络计划时间参数的计算

1）单代号网络计划时间参数计算的公式与规定

（1）工作i的最早开始的计算应符合下列规定：

①工作i的最早开始时间ESi应从网络图的起点节点开始，顺着箭线方向依次逐个计算。

②起点节点的最早开始时间ES1如无规定时，其值等于零，即

③其他工作的最早开始时间ESi应为

式中：ESh——工作i的紧前工作h的最早开始时间；

　　　Dh——工作i的紧前工作h的持续时间。

（2）工作i的最早完成时间EFi的计算应符合下式规定：

（3）网络计划计算工期TC的计算应符合下列规定：

式中：EFn——终点节点n的最早完成时间。

（4）网络计划的计算工期TP应按下列情况分别确定：

①当已规定了要求工期TR时，

②当未规定要求工期时，

（5）相邻两项工作i和j之间的时间间隔LAGi－j的计算应符合下式规定：

式中：ESj——工作j的最早开始时间；

　　　EFi——工作i的最早完成时间。

（6）工作总时差的计算应符合下列规定：

①工作i的总时差TFi应从网络图的终点节点开始，逆着箭线方向依次逐项计算。

②终点节点所代表的工作n的总时差TFn的值为零，即

分期完成的工作的总时差值为零。

③其他工作的总时差TFi的计算应符合下列规定：

式中：TFj——工作i的紧后工作j的总时差。

　　　当已知各项工作的最迟完成时间LFi或最迟开始时间LSi时，工作的总时差TFi计算也应符合下列规定：

（7）工作i的自由时差FFi的计算应符合下列规定：

（8）工作最迟完成时间的计算应符合下列规定：

①工作i的最迟完成时间LFi应从网络图的终点节点开始，逆着箭线方向依次逐项计算。

②终点节点所代表的工作n的最迟完成时间LFn应按网络计划的计划工期TP确定，即

③其他工作i的最迟完成时间LFi应为

式中：LFj——工作i的紧后工作j的最迟完成时间；

　　　Dj——工作i的紧后工作j的持续时间。

（9）工作i的最迟开始时间LSi的计算应符合下列规定：

2）标注形式

单代号网络计划时间参数的概念与双代号网络计划相同。其标注形式如图4－45。

图4－45　单代号网络计划时间参数的标注形式

3）计算步骤与方法

以图4－44所示网络图为例，其时间参数标注及计算结果如图4－46。

图4－46　单代号网络计划的时间参数计算结果

（1）工作最早时间的计算

从起点节点开始，顺箭头方向依次进行。

①最早开始时间

工作的最早开始时间按以下公式计算，各工作的最早开始时间如下：

②最早完成时间

工作的最早完成时间按以下公式计算，各工作的最早完成时间如下：

（2）相邻两项工作时间间隔的计算

相邻工作的时间间隔按以下公式计算，其值计算如下：

（3）工作最迟时间的计算

①最迟完成时间

工作的最迟完成时间按以下公式计算，各工作的最迟完成时间如下：

②最迟开始时间

工作的最迟开始时间按以下公式计算，各工作的最迟开始时间如下：

（4）工作总时差的计算

工作总时差的计算按以下公式进行，计算结果如下：

（5）工作自由时差的计算

工作自由时差的计算按以下公式进行，计算结果如下：

（6）确定关键工作和关键线路

同双代号网络图一样，总时差为最小值的工作是关键工作。当计划工期等于计算工期时，总时差最小值为零，则总时差为零的工作就是关键工作。

单代号网络图的关键线路可以通过工作之间的时间间隔LAGi，j来判断，即自终点节点至起点节点的全部LAGi，j＝0的线路为关键线路。

如图4－46所示，加粗的线路为关键线路。

4．4　双代号时标网络计划

4．4．1　双代号时标网络计划的特点

双代号时标网络计划是以水平时间坐标为尺度编制的双代号网络计划，其主要特点是：

（1）时标网络计划兼有网络计划与横道计划的优点，它能够清楚地表明计划的时间进程，使用方便。

（2）时标网络计划能在图上直接显示出各项工作的开始与完成时间，工作的自由时差及关键线路。

（3）在时标网络计划中可以统计每一个单位时间对资源的需要量，以便进行资源优化和调整。

（4）由于箭线受到时间坐标的限制，当情况发生变化时，对网络计划的修改比较麻烦，往往要重新绘图。但在使用计算机以后，这一问题已较容易解决。

4．4．2　双代号时标网络计划的一般规定

（1）时间坐标的时间单位应根据需要在编制网络计划之前确定，可为季、月、周、天等。

（2）时标网络计划应以实箭线表示工作，以虚箭线表示虚工作，以波形线表示工作的自由时差。

（3）时标网络计划中所有符号在时间坐标上的水平投影位置，都必须与其时间参数相对应。节点中心必须对准相应的时标位置。

（4）虚工作必须以垂直方向的虚箭线表示，有自由时差时加波形线表示。

4．4．3　双代号时标网络计划的绘制方法

时标网络计划一般按工作的最早开始时间绘制，其绘制方法有间接绘制法和直接绘制法。

1）间接绘制法

间接绘制法是先计算网络计划的时间参数，再根据时间参数在时间坐标上进行绘制的方法。其绘制步骤和方法如下：

（1）先绘制双代号网络图，计算时间参数，确定关键工作和关键线路。

（2）根据需要确定时间单位并绘制时标横轴。

（3）根据工作最早开始时间或节点的最早时间确定各节点的位置。

（4）依次在各节点间绘出箭线及时差。绘制时宜先画出关键工作、关键线路，再画非关键工作。如箭线长度不足以达到工作的完成节点时，用波形线补足，箭头画在波形线与节点连接处。

（5）用虚箭线连接各有关节点，将有关的工作连接起来。

2）直接绘制法

直接绘制法是不计算网络计划时间参数，直接在时间坐标上进行绘制的方法。其绘制步骤和方法可归纳为如下口诀：“时间长短坐标限，曲直斜平利相连；箭线到齐画节点，画完节点补波线；零线尽量拉垂直，否则安排有缺陷”。

（1）时间长短坐标限：箭线的长度代表着具体的施工时间，受到时间坐标的制约。

（2）曲直斜平利相连：箭线的表达方式可以是直线、折线、斜线等，但布图应合理，直观清晰。

（3）箭线到齐画节点：工作的开始节点必须在该工作的全部紧前工作都画出后，定位在这些紧前工作最晚完成的时间刻度上。

（4）画完节点补波线：某些工作的箭线长度不足以达到其完成节点时，用波线补足。

（5）零线尽量拉垂直：虚工作持续时间为零，应尽可能让其为垂直线。

（6）否则安排有缺陷：若出现虚工作占据时间的情况，其原因是工作面停歇或施工作业队组工作不连续。

4．4．4　双代号时标网络计划的绘制方法

1）关键线路的确定

自终点节点逆箭线方向朝起点节点观察，自始至终不出现波形线的线路为关键线路。

2）工期的确定

时标网络计划的计算工期，应是其终点节点与起点节点所在位置的时标值之差。

3）时间参数的判定

（1）最早时间参数：按最早时间绘制的时标网络计划，每条箭线的箭尾和箭头所对应的时标值应为该工作的最早开始时间和最早完成时间。

（2）自由时差：波形线的水平投影长度即为该工作的自由时差。

（3）总时差：自右向左进行，其值等于诸紧后工作的总时差的最小值与本工作的自由时差之和，即

（4）最迟时间参数：最迟开始时间和最迟完成时间应按下式计算：

【例4－4】　已知网络计划的资料如表4－3所示，试用直接法绘制双代号时标网络计划。

表4－3　网络计划资料表

【解】　（1）将网络计划的起点节点定位在时标表的起始刻度线的位置上，起点节点的编号为1，如图4－47所示。

（2）画节点①的外向箭线，即按各工作的持续时间，画出无紧前工作的A、B、C工作，并确定节点②、③、④的位置，如图4－47所示。

（3）依次画出节点②、③、④的外向箭线工作D、E、H，并确定节点⑤、⑥的位置。节点⑥的位置定位在其两条内向箭线的最早完成时间的最大值处，即定位在时标值7的位置，工作E的箭线长度达不到⑥节点，则用波形线补足，如图4－47所示。

图4－47　双代号时标网络计划

（4）按上述步骤，直到画出全部工作，确定出终点节点⑧的位置，时标网络计划绘制完毕，如图4－47所示。

（5）关键线路和计算工期的确定

时标网络计划关键线路的确定，应自终点节点逆箭线方向朝起点节点逐次进行判定：从终点到起点不出现波形线的线路即为关键线路。如图4－47中，关键线路是：①—④—⑥—⑦—⑧，用双箭线表示。

时标网络计划的计算工期，应是终点节点与起点节点所在位置之差。如图4－47中，计算工期TC＝14－0＝14（天）。

（6）时标网络计划时间参数的确定

在时标网络计划中，6个工作时间参数的确定步骤如下：

A．最早时间参数的确定

按最早开始时间绘制时标网络计划，最早时间参数可以从图上直接确定。

a．最早开始时间ESi－j

每条实箭线左端箭尾节点（i节点）中心所对应的时标值，即为该工作的最早开始时间。

b．最早完成时间EFi－j

如箭线右端无波形线，则该箭线右端节点（j节点）中心所对应的时标值为该工作的最早完成时间；如箭线右端有波形线，则实箭线右端末所对应的时标值即为该工作的最早完成时间。

如图4－47可知：，以此类推确定。

B．自由时差的确定

时标网络计划中各工作的自由时差值应为表示该工作的箭线中波形线部分在坐标轴上的水平投影长度。

如图4－47中可知，工作E、H、F的自由时差分别为

C．总时差的确定

时标网络计划中工作的总时差的计算应自右向左进行，且符合下列规定：

a．以终点节点（j＝n）为箭头节点的工作的总时差TFi－n应按网络计划的计划工期TP计算确定，即

如图4－47中可知，工作F、J、H的总时差分别为

b．其他工作的总时差等于其紧后工作j－k总时差的最小值与本工作的自由时差之和，即

如图4－47中，各项工作的总时差计算如下：

D．最迟时间参数的确定

时标网络计划中工作的最迟开始时间和最迟完成时间可按下式计算：

如图4－47中，工作的最迟开始时间和最迟完成时间为

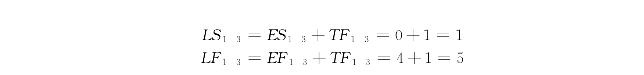
以此类推，可计算出各项工作的最迟开始时间和最迟完成时间。由于所有工作的最早开始时间、最早完成时间和总时差均为已知，故计算容易，此处不再一一列举。

4．5　网络计划优化概述

经过调查研究，确定施工方案、划分施工过程、分析施工过程间的逻辑关系、编制施工过程一览表、绘制网络图、计算时间参数等步骤，可以确定网络计划的初始方案。然而，要使工程计划顺利实施，获得缩短工期、质量优良、资源消耗小、工程成本低的效果，就要按一定标准对网络计划初始方案进行衡量，必要时还需进行优化调整。

网络计划的优化，就是在满足既定约束条件下，按选定目标，通过不断改进网络计划寻求满意方案。

网络计划的优化目标，应按计划任务的需要和条件选定，包括工期目标、费用目标、资源目标。

网络计划的优化，按工期需达到的目标不同，一般分为工期优化、费用优化、资源优化。

4．5．1　工期优化

工期优化是指在满足既定约束条件下，按要求工期目标，通过延长或缩短网络计划初始方案的计算工期，以达到要求工期目标，保证按期完成任务。

网络计划的初始方案编制好后，将计算工期与要求工期相比较，会出现以下情况：

1）计算工期小于或等于要求工期

如果计算工期小于要求工期不多或两者相等，则一般不需要工期优化。

如果计算工期小于要求工期较多，则考虑与施工合同中的工期提前奖等条款相结合，确定是否进行工期优化。若需优化，优化的方法是：延长关键线路上资源占用量大或直接费用高的工作的持续时间（相应减少其单位时间资源需要量）；或重新选择施工方案，改变施工机械，调整施工顺序，再重新分析逻辑关系；编制网络图，计算时间参数；反复多次进行，直至满足要求工期。

2）计算工期大于要求工期

计算工期大于要求工期时，可以在不改变各项工作的逻辑关系的前提下，通过压缩关键工作的持续时间来满足要求工期。压缩关键工作的持续时间的方法，有顺序法、加数平均法、选择法等。顺序法是指按关键工作开工时间来确定需压缩的工作，先做的先压缩。加数平均法是按关键工作持续时间的百分比压缩。这两种方法虽然简单，但没有考虑压缩的关键工作所需要的资源是否有保证及相应的费用增加幅度。选择法更接近实际需要，下面重点介绍。

（1）选择应缩短持续时间的关键工作时，应考虑下列因素：

①缩短持续时间对安全和质量影响不大的工作。

②有充足备用资源的工作。

③缩短持续时间对所增加费用最小的工作。

将所有工作按其是否满足上述三方面要求确定优选系数，优选系数小的工作较适宜压缩。选择关键工作并压缩持续时间时，应选择优选系数最小的工作。若需要同时压缩多个关键工作的持续时间时，则它们的优选系数之和（组合优选系数）最小应优先作为压缩对象。

（2）工期优化的计算，应按下述步骤进行：

①计算并找出初始网络计划的计算工期TC及关键线路和关键工作。

②按要求工期TR计算应缩短的时间

③确定各关键工作能缩短的持续时间。

④按前述要求的因素选择关键工作，压缩其持续时间，并重新计算网络计划的计算工期。此时，要注意不能将关键工作压缩成非关键工作。当出现多条关键线路时，必须将平行的各关键线路的持续时间压缩相同的数值；否则，不能有效地缩短工期。

⑤当计算工期仍超过要求工期时，则重复以上步骤，直到满足要求工期或不能再压缩为止。

⑥当所有关键工作的持续时间都已达到其能缩短的极限而工期仍不能满足要求工期时，应对计划的原技术方案、组织方案进行调整，或对要求工期重新审定。

下面结合实例说明工期优化的计算步骤。

【例4－5】　已知某工程双代号网络计划如图4－48所示，其中箭线上下方标注内容，箭线上方括号外为工作名称，括号内为优选系数；箭线下方括号外为工作正常持续时间，括号内为最短持续时间。现假定要求工期为10天，试对其工期进行优化。

图4－48　某工程双代号网络计划

【解】　按下列步骤进行：

（1）用简便方法计算工作正常持续时间时，网络计划的时间参数如图4－49所示，标注工期、关键线路，其中关键线路用粗箭线表示。计算工期TC＝16天。

（2）按要求工期TR计算应缩短的时间ΔT。

（3）选择关键线路上优选系数较小的工作，依次进行压缩，直到满足要求工期。

①第一次压缩，根据图4－49中数据，选择关键线路上优选系数最小的工作4—6工作，可压缩2天，则5—6工作也成为关键工作，压缩后网络计划如图4－50所示。

图4－49　初始网络计划时间参数

图4－50　第一次压缩后的网络计划

②第二次压缩，根据第一次压缩后的数据，选择关键线路上优选系数最小的1—2工作，可压缩1天，则1—3工作也成为关键工作，压缩后网络计划如图4－51所示。

图4－51　第二次压缩后的网络计划

③第三次压缩，根据第二次压缩后的数据，选择关键线路上优选系数最小的3—4工作，只能压缩1天，此时3—5工作也成为关键工作，压缩后网络计划如图4－52所示。

图4－52　第三次压缩后的网络计划

④第四次压缩，根据第三次压缩后的数据，选择关键线路上组合优选系数最小的工作1—3和2—3，且只能压缩1天，压缩后网络计划如图4－53所示。

图4－53　第四次压缩后的网络计划

⑤第五次压缩，根据第四次压缩后的数据，只能选择关键线路上的组合工作3—4、3—5，且压缩1天后才能达到计划工期，优化后的网络计划如图4－54所示。

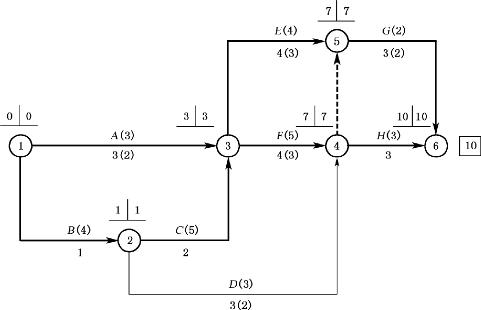
图4－54　优化后的网络计划

4．5．2　费用优化

费用优化又称工期成本优化或时间成本优化，是寻求工程总成本最低时的工期安排或按要求工期寻求最低成本的计划安排过程。

1）费用和时间的关系

工程项目的总费用由直接费用和间接费用组成。直接费用由人工费、材料费、机械使用费及现场经费等组成。施工方案不同，则直接费用不同，即使施工方案相同，工期不同，直接费也不同。间接费用包括企业经营管理的全部费用。

一般情况下，缩短工期会引起直接费用的增加和间接费用的减少，延长工期会引起直接费用的减少和间接费用的增加。在考虑工程总费用时，还应考虑工期变化带来的其他损益，包括因拖延工期而罚款或提前竣工而得到的奖励，甚至也考虑因提前投产而获得的收益和资金的时间价值等。

工期和费用的关系如图4－55所示，图中工程总费用曲线是由直接费用曲线和间接费用叠加而成。曲线上的最低点就是工程计划的最优方案之一，此方案工程成本最低，相对应的工程持续时间成为最优工期。

图4－55　工期－费用关系示意图

图4－56　时间与直接费的关系示意图

（1）直接费用曲线

直接费用曲线通常是一条由左上向右下的下凸曲线，如图4－56所示，因为直接费用总是随着工期的缩短而更快增加的，在一定范围内与时间成反比关系。如果缩短工期，即加快施工速度，要采取加班加点和多班作业，采用高价的施工方法和机械设备等，直接费用也跟着增加。然而工作时间缩短至某一极限，则无论增加多少直接费用也不能再缩短工期，此极限为临界点，此时的时间称为最短持续时间，此时费用为最短时间直接费用。反之，如果延长时间，则可减少直接费用。然而时间延长至某一极限，则无论将工期延长多少，也不能再减少直接费用，此极限为正常点，此时的时间称为正常持续时间，此时的费用称为正常时间直接费用。连接正常点与临界点的曲线，称为直接费用曲线。直接费用曲线并不像图中那样圆滑，而是由一系列线段组成的折线并且越接近最高费用（极限费用）其曲线越陡。为了计算方便，可以近似的将它假定为一条直线，如图4－56所示。我们把因缩短工作持续时间（赶工）每一单位时间所需增加的直接费用，简称为直接费用率，按以下公式计算：

式中:ΔC_i-j——工作i－j的直接费用率；

　　CC_i-j——将工作i－j持续时间缩短为最短持续时间后，完成该工作所需的直接费用；

　　CN_i-j——在正常条件下完成工作i－j所需的直接费用；

　　DN_i-j——工作i－j的正常持续时间；

从公式中可以看出，工作的直接费用率越大，将工作的持续时间缩短一个时间单位，相应增加的直接费用就越多；反之，工作的直接费用率越小，则将该工作的持续时间缩短一个时间单位，相应增加的直接费用就越少。

根据各工作的性质不同，其工作持续时间和费用之间的关系通常有以下两种情况：

①连续变化型关系。有些工作的直接费用随着工作持续时间的改变而改变，如图4－56所示。介于正常持续时间和最短（极限）时间之间的任意持续时间的费用可根据其费用斜率，用数学方法推算出来。这种时间和费用之间的关系是连续变化的，成为连续型变化关系。

例如，某工作经过计算确定其正常持续时间为10天，所需费用为1　200元，在考虑增加人力、材料、机具设备和加班的情况下，最短时间为6天，而费用为1　500元，则其单位变化率为

即每缩短1天，其费用增加75元。

②非连续型变化关系。某些工作的直接费用与持续时间之间的关系是根据不同施工方案分别估算出来的，因此，介于正常持续时间与最短持续时间之间的关系不能用线性来表示，不能通过数学方法计算，工作不能逐天缩短，在图上表现为几个点，只能在几种情况中选择一种，如图4－57所示。

图4－57　非连续型的时间直接费用关系示意图

例如，某土方开挖工程采用3种不同的开挖机械，其费用和持续时间见表4－5所示。

因此，在确定施工方案时，根据工期要求，只能在表4－4中的3种不同机械中选择，在图中也就是只能取其中3点中的一点。

表4－4　时间及费用表

（2）间接费用曲线

表示间接费用与时间成正比关系的曲线，其斜率表示间接费用在单位时间内的增加或减少值。间接费用与施工单位的管理水平、施工条件、施工组织等有关。

2）费用优化的方法步骤

费用优化的基本方法：不断在网络计划中找出直接费用率（或组合直接费用率）最小的关键工作，缩短其持续时间，同时考虑间接费用随工期缩短而减少的数值，最后求得工程总成本最低时的最优工期安排或按要求工期求得最低成本的计划安排。费用优化的基本方法可简化为以下口诀：不断压缩关键线路上有压缩可能且费用最少的工作。

按照上述基本方法，费用优化可按以下步骤进行：

（1）按工作的正常持续时间确定计算关键线路、工期、总费用。

（2）按公式（4－1）计算各项工作的直接费用率。

（3）当只有一条关键线路时，应找出直接费用率最小的一项关键工作，作为缩短持续时间的对象；当有多条关键线路时，应找出组合直接费用率最小的一组关键工作，作为缩短持续时间的对象。

（4）对于选定的压缩对象（一项关键工作或一组关键工作），首先比较其直接费用率或组合直接费用率与工程间接费用率的大小：

①如果被压缩对象的直接费用率或组合直接费用率小于工程间接费用率，说明压缩关键工作的持续时间会使工程总费用减少，故应压缩关键工作的持续时间。

②如果被压缩对象的直接费用率或组合直接费用率等于工程间接费用率，说明压缩关键工作的持续时间不会使工程总费用增加，故应压缩关键工作的持续时间。

③如果被压缩对象的直接费用率或组合直接费用率大于工程间接费用率，说明压缩关键工作的持续时间会使工程总费用增加，此时应停止缩短关键工作的持续时间，在此之前的方案即为优化方案。

（5）当需要缩短关键工作的持续时间时，其缩短值的确定必须符合下列两条规则：

①缩短后工作的持续时间不能小于其最短持续时间。

②缩短持续时间的工作不能变成非关键工作。

（6）计算关键工作持续时间缩短后相应的总费用变化。

（7）重复（3）～（6）步，直至计算工期满足要求工期，或被压缩对象的直接费用率大于工程间接费用率为止。费用优化过程见表4－5。

表4－5　费用优化过程表

注：费率差＝（直接费用率或组合直接费用率－间接费用率）；
压缩需要总费用＝费率差×缩短时间；
总费用＝上次压缩后总费用＋本次压缩需用总费用；
工期＝上次压缩后工期－本次压缩时间。

下面结合实例说明费用优化的计算步骤。

【例4－6】　已知某工程网络计划图如图4－58所示，图中箭线上方为工作的正常持续时间的直接费用和最短时间的直接费用（以万元为单位），箭线下方为工作的正常持续时间和最短持续时间（天）。其中3—5工作的时间与直接费用为非连续型变化关系，其正常时间及直接费用为（5天，8万元），最短时间及直接费用为（3天，9万元）。整个工程计划的间接费用率为1．5万元／天，最短工期时的间接费用为8万元。试对此计划进行费用优化，确定工期－费用关系曲线，求出费用最少的相应工期。

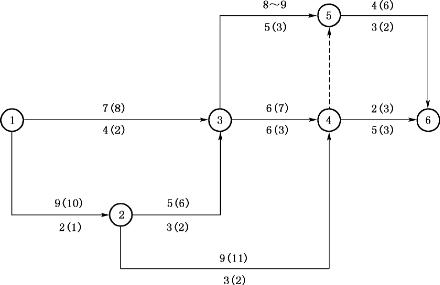
图4－58　某工程双代号网络计划

【解】　（1）按各项工作的正常持续时间，用简便方法确定计算工期、关键线路、总费用，如图4－59所示。计算工期为16天，关键线路为1—2—3—4—6。

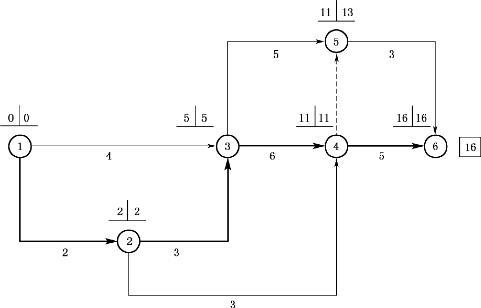
图4－59　初始网络计划关键线路

按各项工作的最短持续时间，用简捷方法确定计算工期，如图4－60所示。计算工期为9天。

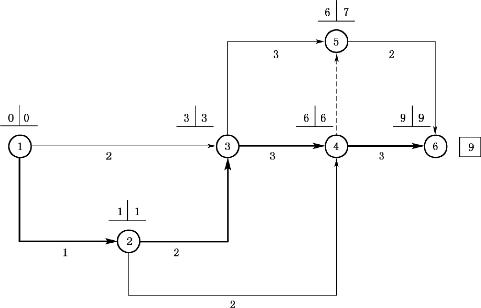
图4－60　工作最短时间关键线路

正常持续时间时的总直接费用＝各项工作正常持续时间时的直接费用之和＝8＋4＋7＋6＋2＋9＋5＋9＝50（万元）

正常持续时间时的总间接费用＝最短工期时的总间接费用＋（正常工期－最短工期）×间接费率＝8＋（16－9）×1．5＝18．5（万元）

正常持续时间的总费用＝正常持续时间时总直接费用＋正常持续时间总间接费用＝50＋18．5＝68．5（万元）

（2）按公式（4－1）计算各项工作的直接费用率，见表4－6。

表4－6　各项工作直接费用率

（3）不断压缩关键线路上有压缩可能且费用最少的工作，进行费用优化，压缩过程的网络图如图4－61～图4－63所示。

①第一次压缩

从图4－59可知，该网络计划的关键线路上有4项工作，有4个压缩方案：

压缩工作1—2，直接费用率为1万元／天；

压缩工作2—3，直接费用率为1万元／天；

压缩工作3—4，直接费用率为0．3万元／天；

压缩工作4—6，直接费用率为0．5万元／天。

在上述压缩方案中，由于工作3—4的直接费用率最低，故应选择3—4为压缩对象。工作3—4的直接费用率为0．3万元／天，小于间接费用率1．5万元／天，说明压缩工作3—4可以使工程总费用降低。将工作3—4的工作时间缩短3天，则工作3—5、5—6也成为关键工作，第一次压缩后的网络计划如图4－61所示。图中箭线上方的数字为工作的直接费率（工作3—5除外）。

图4－61　第一次压缩的网络计划

②第二次压缩

从图4－61可知，该网络计划有3条关键线路，为了缩短工期，有以下4个压缩方案（工作3—4不能再压缩，工作5—6的直接费用率大于间接费用率）：

压缩工作1—2，直接费用率为1万元／天；

压缩工作2—3，直接费用率为1万元／天；

压缩工作3—5，可压缩2天，共增加直接费1万元，平均每天增加直接费0．5万元；

压缩工作4—6，直接费用率为0．5万元／天。

在上述压缩方案中，虽然工作3—5、4—6的直接费用率最低，但它们被压缩后变成非关键工作，所以不能压缩。故应选择1—2或2—3为压缩对象，它们的直接费用率均小于间接费用率1．5万元／天，说明压缩工作1—2或2—3可以使工程总费用降低。我们先把工作1—2压缩1天，则工作1—3也成为关键工作，第二次压缩后的网络计划如图4－62所示。

图4－62　第二次压缩的网络计划

③第三次压缩

从图4－62可知，该网络计划有6条关键线路，为了缩短工期，有以下5个压缩方案：

压缩工作1—3，直接费用率为0．5万元／天；

压缩工作2—3，直接费用率为1万元／天；

压缩组合工作1—3和2—3，组合直接费用率为1．5万元／天；

压缩工作3—5，可压缩2天，共增加直接费用1万元，平均每天增加直接费用0．5万元；

压缩工作4—6，直接费用率为0．5万元／天。

在上述压缩方案中，压缩工作1—3、2—3、3—5、4—6后都变成非关键工作，所以不能压缩。所以只能压缩组合工作1—3和2—3，组合工作1—3和2—3的组合直接费用率为1．5万元／天，等于间接费用率1．5万元／天，说明压缩组合工作1—3和2—3虽然不能使工程总费用降低，但总工期可降低。我们把组合工作1—3和2—3压缩1天，第三次压缩后的网络计划如图4－63所示。到此为止，或因工作被压缩后变成非关键工作，或因压缩后费用增加，那么该网络图再压缩下去没有任何意义，所以该次压缩后的方案即为最优方案。具体费用优化过程见表4－7。

表4－7　费用优化过程表

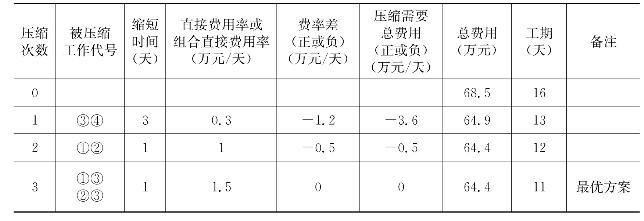
图4－63　第三次压缩的网络计划

4．5．3　资源优化

资源是为了完成一项计划任务所需投入的人力、材料、机械设备和资金等的统称。资源限量是单位时间内可供使用的某种资源的最大数量。完成一项工程任务所需要的资源量基本上是不变的，不可能通过资源优化将其减少。资源优化的目的是通过改变工作的开始和完成时间，使资源按照时间的分布符合优化目标。

在通常情况下，网络计划的资源优化分为两种，即“资源有限—工期最短”的优化和“工期固定—资源均衡”的优化。前者是在满足资源限制条件下，通过调整计划安排，使工期延长最少的过程；而后者是在工期保持不变的条件下，通过调整计划安排，使资源需要量尽可能均衡的过程。具体优化内容在此不再举例。

思考题

1．简述网络计划与横道计划的优缺点。

2．什么是双代号网络计划和单代号网络计划？

3．组成双代号网络图的三要素是什么？各自的含义和特征。

4．什么是关键线路？

5．网络计划有哪几种逻辑关系？

6．简述双代号网络图的绘制规则。

习题

1．试指出如图4－64所示网络图的错误。

图　4－64

2．按下列工作的逻辑关系，分别绘制出双代号网络图。

（1）A、B均完成后进行C、D，D完成后进行E，C、E完成后进行F，F完成后进行G。

（2）A、B、C均完成后进行D，A、B完成后进行E，D、E完成后进行F。

3．根据表4－8所示各工作逻辑关系，试绘制双代号网络图。

表　4－8

4．按表4－9给出的工作和工作持续时间，绘出双代号网络图，并计算各工作的时间参数。

表　4－9

5．已知某工程网络计划，图中箭线下方括号外数据为工作正常作业时间，括号内数据为工作最短持续时间，合同工期为120天，假定工作3—4有充足的资源，且缩短时间对质量无太大影响，工作4—6缩短所需费用最省，且资源充足，工作1—3缩短时间的有利因素不如工作3—4与工作4—6。试对比计划进行工期优化。

图　4－65