2 投影的基本知识
投影是工程制图的基本概念,工程上所用的各种图样都是用投影的方法绘制的,根据对象及目的的不同,采用不同的投影方法:中心投影法和平行投影法。要学好工程制图,就必须了解和掌握投影法的基本原理及按这些原理所形成的各种图样的绘制和阅读方法。
2.1 投影的形成和分类
2.1.1 投影的形成
生活中,我们随处可见影子这个自然现象。在光线(阳光或者灯光)的照射下,物体会在地面、墙面或者其他表面投射影子,而且随着光线方向的不同,影子也会发生变化,如图2-1(a)所示。
人们对自然界的这一物理现象加以科学的抽象和概括,假设光线能够穿透物体,将物体的轮廓线投射在某个面上的影子绘制成“线框图”,把这样形成的线框图称为投影图,简称投影。如图2-1(b)所示。 研究物体与投影之间的关系就是投影法。下面介绍有关投影法的几个基本概念,如图2-2所示。投影中心:光源S抽象为一点,称为投影中心。
投影线:从光源S射出的任意一条直线,称为投影线或投射线 。
投影面:投影所在的平面,称为投影面。
投影:通过物体上任意一点的光线与投影面的交点,称为该点在投影面上的投影。


图2-1 影子与投影
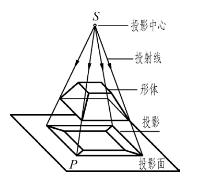
图2-2 中心投影

图2-3 平行投影
2.1.2 投影的分类
根据投影线之间的相互关系,可分为中心投影和平行投影 。
1)中心投影
假设投影中心S在有限的范围之内,所有的投影线都交于一点,这种方法所产生的投影,称为中心投影 。如图2-2所示。
用中心投影法绘制的投影图具有立体感和真实感,符合人的视觉感官,因此在建筑(或装修)设计的初始阶段,往往用这种图样告诉人们设计师的意图,便于尽早调整设计方案。
2)平行投影
假设将投影中心S移动到离投影面无穷远的地方,则投影线在无穷远处相交,可视为平行,由此产生的投影,称为平行投影 。如图2-3所示。
根据投影线和投影面的相对位置的不同,平行投影又可分为斜投影和正投影。
投影线与投影面倾斜时的投影,称为斜投影,如图2-3(a)所示。
投影线与投影面垂直时的投影,称为正投影,如图2-3(b)所示。
2.2 工程中常用的几种投影图
根据对象、作用和表达目的的不同,工程上常用的图样有:多面正投影图、轴测投影图、透视投影图和标高投影图。

图2-4 多面正投影图
(1)多面正投影图,就是用平行正投影法将物体向多个方向投影,以反映物体不同方向的形状和大小。这是工程中应用最为广泛的一种图样,本书在以后没有特别申明的情况下,所说投影就是这种正投影。
优点:能准确地反映物体的形状和大小,度量性好,作图简便。
缺点:立体感差,不易看懂,如图2-4所示。
(2)轴测投影图,是物体在一个投影面上的平行投影图,简称轴测图。该种投影图具有较强的立体感,工程设计中常作为一种辅助图样,帮助正投影图形象地表达物体的形状,如图2-5所示。本书将在第5章中介绍。
优点:图的立体感强,容易看懂。
缺点:投影变形,度量性差,且作图比较麻烦。
(3)透视投影图,是物体在一个投影面上的中心投影图,简称透视图。如图2-1(b)所示。这种图直观感最好,符合人们的视觉效果,常配以材质、色彩和配景,以表达建筑(或装修)设计的效果,所以也称为效果图,如图2-6所示。本书在第8章将介绍透视图的原理和画法,第14、15章将分别介绍用计算机实现这样的效果图及效果图的艺术处理。

图2-5 轴测投影图
(4)标高投影图,这是一种加注了高程的水平投影图,一般与地形图结合以表达建筑物与地面的关系,如图2-7所示。本书将在第7章中介绍。

图2-6 建筑效果图(添加材质和色彩的透视图)

图2-7 标高投影图
2.3 正投影的特性与基本原理
2.3.1 正投影的特性
1)真实性
当直线或平面平行于投影面时,其正投影反映实长或者实形。如图2-8所示,直线AB和三角形CDE平行于投影面H,它们在H面上的投影分别反映实长(ab=AB)和实形(△cde≌△CDE)。这种性质称为真实性 。
2)积聚性
当直线或平面垂直于投影面时,其正投影积聚为一点或者一条直线,如图2-9所示。这种性质称为积聚性 。

图2-8 真实性投影

图2-9 积聚性投影
3)类似性
当直线或平面倾斜于投影面时,直线的正投影仍然是直线,但小于实长;平面的投影小于实形,但是形状相像(不存在相似比),如图2-10所示。这种性质称为类似性。
4)平行性
当空间两直线相互平行时,它们在同一平面上的投影仍然平行。而且它们投影的长度之比等于空间两直线的长度之比。如图2-11所示,AB∥CD,ab∥cd,且AB∶CD=ab∶cd。这种性质称为平行性 。

图2-10 类似性投影

图2-11 平行性投影
2.3.2 正投影图的原理
任何物体都具有三维方向的尺度,如何在平面图纸上真实地表达出物体的长、宽、高的尺寸和形状,以及如何根据平面图纸想象、还原出物体的空间形状,是工程制图要解决的主要问题。
一般情况下,要用3个不同方向的投影图才能将物体的空间形状表达清楚,为此常设3个投影面构成一个三面投影体系。
1)三面投影体系的建立
如图2-12(a)所示,设立3个互相垂直的平面作为投影面,组成一个三面投影体系:
水平投影面用H标记,简称水平面或H·面。
正立投影面用V标记,简称正立面或V·面。
侧立投影面用W标记,简称侧立面或W·面 。
3个投影面的交线,称为投影轴 。它们分别用OX、OY、OZ表示。
OX轴:V面和H面的交线,代表物体的长度方向。
OY轴:H面和W面的交线,代表物体的宽度方向。
OZ轴:V面和W面的交线,代表物体的高度方向。
3个投影轴的交点,称为原点 。
将物体放入三面投影体系,并置于观察者与投影面之间,然后将物体分别向3个投影面作投影,得到3个投影图。它们分别把物体的长、宽、高3个方向和左右、前后、上下6个方位的形状和位置关系表达了出来。其形成方式如下所述:
从上向下投影,在H面上得到水平投影图,简称水平投影或H·投影 ,也称俯视图 。
从前向后投影,在V面上得到正面投影图,简称正面投影或V·投影 ,也称正视图 。
从左向右投影,在W面上得到侧面投影图,简称侧面投影或W·投影 ,也称侧视图 。
2)三面投影图的展开
在实际应用中,是在一个平面上表达3个方向的投影图,因此,需要将三面投影体系展开:假设V面不动,H面绕着OX轴向下旋转90°,W面绕着OZ轴向后旋转90°,如图2-12(b)所示。
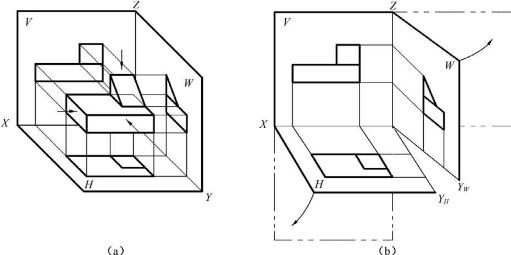
图2-12 三面投影的形成与展开
展开后,H面投影在V面投影的正下方,W面投影在V面投影的正右方,如图2-13(a)所示。
注意:OY轴旋转后出现了两个位置:随H面旋转到OYH位置;随W面旋转到OYW位置。
实际绘图时,为使作图简便和图面清晰,一般不画表示投影面的边框线,也不注写V、H、W字样,对于立体的投影,一般也不画投影轴。这种不画投影面的边框线和投影轴的图样,称为“无轴投影”。如图2-13(b)所示。

图2-13 三面投影的方位关系和投影规律
3)三面投影图的投影规律
从图2-13可以看出:V面投影和H面投影都反映了物体的长度;V面投影和W面投影都反映了物体的高度;W面投影和H面投影都反映了物体的宽度。因此,三面投影图之间存在下述投影关系:
V面投影与H面投影——长对正 。
V面投影与W面投影——高平齐 。
W面投影和H面投影——宽相等。
“长对正”、“高平齐”、“宽相等”的投影关系是三面投影图之间的重要特性,也是以后绘图和读图时必须遵守的最基本的投影规律——简称“三等规律”。
绘制三面投影图时应注意:为符合“三等规律”,投影图之间的作图联系线用细实线绘制,物体的可见轮廓线最后要画为粗实线,不可见的轮廓线用虚线表示(虚线和实线重合时只画实线)。
2.4 点、直线、平面的投影
任何空间形体都是由点、线、面等几何元素所构成的,研究点、线、面的投影规律是掌握空间形体投影规律的基础。
2.4.1 点的投影
1)点的三面投影及其特性
(1)点的三面投影
首先建立一个H、V、W三面投影体系,将空间点A置于三面投影体系中,过A点向H、V、W面作投射线,分别得到交点a、a′、a″。a称为点A的水平投影(H面投影),a′称为点A的正面投影(V面投影),a″称为点A的侧面投影(W面投影)。如图2-14(a)所示。
然后将3个投影面展开到一个平面内:V面不动,将H面绕着OX轴向下旋转90°,W面绕着OZ轴向后旋转90°,就得到了点A的三面投影图,如图2-14(b)所示。为了简化作图,投影面边框线往往不画,并作45°斜线为作图辅助线,用来保证H面和W面投影的对应关系,如图2-14(c)所示。

图2-14 点的三面投影
(2)点的三面投影的投影特性
在图2-14(a)中,投射线Aa、Aa′形成一个矩形平面Aaaxa′,该平面与H面、V面互相垂直且交OX轴于ax。可以证明,a′ax⊥OX,aax⊥OX,则展开后a′a⊥OX,如图2-14(b)所示。同时,因为平面Aaaxa′是一个矩形,则有Aa=a′ax,Aa′=aax。
同理可得:a′a″⊥OZ;aaYH⊥OYH,a″aYW⊥OYW……
综上所述,可得出点的三面投影的投影规律:
①点的投影连线垂直于相关的投影轴 。即:
点A的H面投影与V面投影连线垂直于投影轴X轴——aa′⊥OX。
点A的V面投影与W面投影连线垂直于投影轴Z轴——a′a″⊥OZ。点A的H面投影与W面投影有:aaYH⊥OYH,a″aYW⊥OYW。
②点的投影到投影轴的距离,等于空间点到相关的投影面的距离 。即:
Aa=a′ax=a″ayW,等于空间点A到H投影面的距离。
Aa′=aax=a″az,等于空间点A到V投影面的距离。
Aa″=a′az=aayH,等于空间点A到W投影面的距离。
显然,点的两面投影即可唯一确定点的空间位置。由点的任意两面投影,运用上述投影特性,便可求出点的第三个投影。
【例2-1】 已知A、B点的两面投影,求作其第三面投影,如图2-15(a)所示。
【解】 根据点的投影规律,由点的两面投影可以求出点的第三个投影。具体作法如图2-15(b)所示:
过a作水平线与45°辅助线相交,再由交点向上作铅垂线,与过a′向右所作的水平线相交的交点即为a″。
同理,过b″作铅垂线与45°辅助线相交,再由交点向左作水平线,与过b′向下所作的铅垂线相交于b。

图2-15 求作点的第三个投影
2)两点的相对位置
(1)点的坐标
点的空间位置可以用直角坐标来确定。空间点A的坐标可表示为A(x,y,z),x坐标表示A点到W面的距离x=Aa″,y坐标表示A点到V面的距离y=Aa′,z坐标表示A点到H面的距离z=Aa。如图2-16所示。

图2-16 空间点的坐标
当点的3个坐标中有一个坐标为零,则该点位于某一投影面上。如图2-17所示,点A 的z坐标为零,则A点位于H面上;点B的y坐标为零,则点B位于V面上;点C的x坐标为零,则C点位于W面上。投影面上的点,其一个投影与自身重合,另两个投影在相应的投影轴上。

图2-17 投影面上点的三面投影
当点的3个坐标中2个坐标为零,则该点位于某一投影轴上。如图2-18所示,点D的y、z坐标均为0,则D点位于X轴上;点E的x、y坐标均为0,则E点位于Z轴上;点F的x、z坐标均为0,则F点位于Y轴上。投影轴上的点,其1个投影在原点,另2个投影在相应的投影轴上。
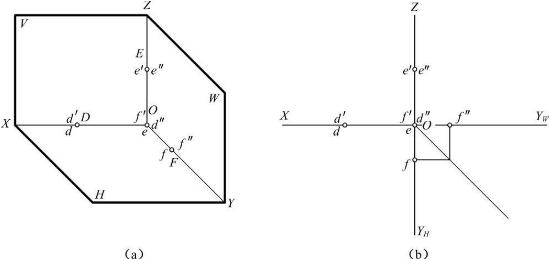
图2-18 投影轴上点的三面投影
【例2-2】 已知点A(20,8,14),作其三面投影图。
【解】 作图步骤如下:
①以原点O为起点,在坐标轴OX、OYH、OZ上分别截取长度20mm、8mm、14mm,得到点ax、ayH、az,如图2-19(a)所示。
②过点ax、az分别作坐标轴OX、OZ的垂线,两垂线的交点为a′;过点ayH作水平线,左边与a′ax的交点为a,右边与45°辅助线相交,过交点向上引垂线,该垂线与a′az的交点为a″,如图2-19(b)所示。

图2-19 已知点的坐标求作点的三面投影
(2)两点的相对位置
两点的相对位置可以用点的坐标值的大小来判定。x坐标反映两点的左右关系,大者在左边,小者在右边;y坐标反映两点的前后关系,大者在前边,小者在后边;z坐标反映两点的上下关系,大者在上边,小者在下边。一般以x、y、z坐标的顺序来判定两点的相对位置关系。
【例2-3】 如图2-20(a)所示,已知A、B两点的三面投影图,判断两点的相对位置关系,并画出两点的直观图。
【解】 由图2-20(a)可知,B点的x坐标大于A点,y坐标小于A点,z坐标大于A点,因此A、B两点的相对位置为B点在A点的左边、后边和上边,称为B点在A点的左后上方。按各坐标作出其直观图,如图2-20(b)所示。

图2-20 两点的相对位置关系
(3)重影点及其可见性
如果空间两点的某两个坐标相同,两点位于某一投影面的同一投射线上,则两个点在这个投影面上的投影重合,这两点称为该投影面的重影点 。对于重影点需判别其可见性,投射线先遇到的点可见,后遇到的不可见,将不可见点的投影加上括号表示。各投影面的重影点如表2-1所示。
表2-1 投影面的重影点

综上所述,各投影面的重影点的可见性判断规律为:上遮下,左遮右 ,前遮后 。
2.4.2 直线的投影
一条直线的空间位置可由直线上的两点的空间位置来确定。因此,一条直线的投影,也可由直线上的两点的投影来确定。一般情况下,用线段的两个端点的投影连线来确定直线的投影。
根据直线对投影面的相对位置的不同,可将直线分成3种:投影面垂直线、投影面平行线和一般位置直线。下面依次介绍每一种直线的投影特性。
1)投影面垂直线
投影面垂直线是指与某一个投影面垂直的直线(必然平行于其他两个投影面),它又可以分为3种:铅垂线 ——垂直于H面而平行于V、W面;正垂线——垂直于V面而平行于H、W面;侧垂线 ——垂直于W面而平行于V、H面。
投影特性:投影面垂直线在所垂直的投影面上的投影积聚成一个点(积聚性 ),另两个投影平行于相关的投影轴 ,且反映实长 (真实性 )。如表2-2所示。
表2-2 投影面平行线

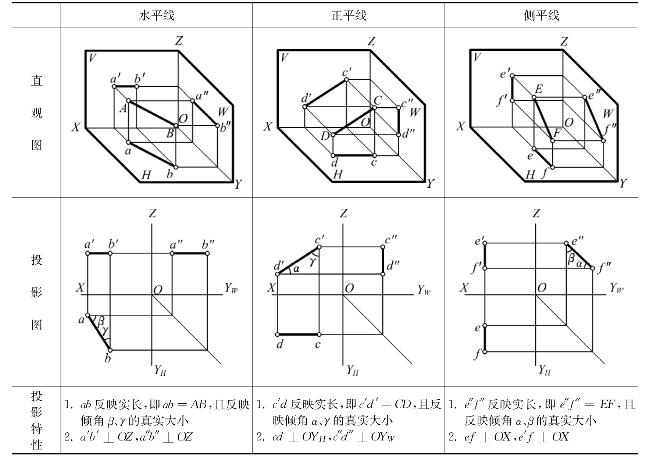
2)投影面平行线
投影面平行线是指与某一个投影面平行而倾斜于另外两个投影面的直线,它又可以分为3种:水平线 ——平行于H面而倾斜于V、W面;正平线 ——平行于V面而倾斜于H、W面;侧平线 ——平行于W面而倾斜于V、H面。
投影特性:投影面平行线 ,在所平行的投影面上的投影反映实长 ,且该投影与相应投影轴的夹角反映直线与另两个投影面的倾角(直线对 H·、V·、W·面的倾角分别用字母 α·、β·、γ·表示 );另外两个投影垂直于相关的投影轴 。如表2-3所示。
表2-3 投影面平行线

续表2-3
3)一般位置直线
一般位置直线是指与3个投影面都倾斜的直线。
如图2-21(a)所示,一般位置直线与H面、V面、W面的倾角分别为α、β、γ,它们既不等于0°也不等于90°。由2-21(b)可知,一般位置直线的三面投影ab、a′b′、a″b″均为斜线,投影长度均小于直线实长;投影与投影轴的夹角不能反映直线对投影面倾角的真实大小。但是可以通过作图求出其实长和倾角实形,此方法通常称为直角三角形法 。

图2-21 一般位置直线的三面投影
如图2-22(a)所示,由A1B∥ab,可得△AA1B为直角三角形。其中,AB为斜边,其长度即直线的实长;A1B为一条直角边,A1B=ab,∠ABA1=α;AA1为另一条直角边,其长度为A、B两点z坐标的差值Δz。为了求出直线AB的实长和倾角α,只要能作出Rt△AA1B即可。
如图2-22(b)所示,ab、a′b′分别为AB的H面、V面投影。在H面投影上,以ab为一直角边,过a作其垂线,并截取aa1=Δz,aa1为另一直角边,连接ba1,得到Rt△aa1b。显见,Rt△aa1b全等于Rt△AA1B,因此ba1为直线AB的实长,∠aba1为直线与H面的倾角α。
同理可求β角,由AB1∥a′b′可得△AB1B为直角三角形。其中,AB为斜边,其长度即直线的实长;AB1为一条直角边,AB1=a′b′,∠BAB1=β;BB1为另一条直角边,其长度为A、B两点y坐标的差值Δy。如图2-22(c)所示,以a′b′为一直角边,过b′作其垂线,并截取b′b1=Δy,b′b1为另一直角边,连接a′b1,得到Rt△a′b1b′。显见,Rt△a′b1b′全等于Rt△AB1B,因此a′b1为直线AB的实长,∠b1a′b′为直线与V面的倾角β。

图2-22 求直线的实长及倾角
至于倾角γ,只要作出W投影,就可以用同样的方法作出其直角三角形,请读者自己完成。需要注意的是各直角边的含义和倾角γ的位置。
根据上述作图的分析,可以总结出构成直角三角形法的4·个要素 :
(1)三角形的一个直角边为一投影长 。
(2)三角形的另一个直角边为线段的 “第三坐标差 ”:H·面上为 Δ·z·、V·面上为 Δ·y·、W·面上为 Δ·x·。
(3)三角形的斜边是线段的实长 。
(4)斜边与投影长的夹角为对应的倾角实形 。
4)直线上的点
直线是点的结合,所以直线上点的投影有如下特性:
(1)从属性 :点K在直线AB上,则点K的三面投影在直线AB的各同面投影上,并符合点的投影规律。反之,若点K的三面投影在直线AB的各同面投影上,并符合点的投影规律,则点C在直线AB上,如图2-23所示。

图2-23 直线上点的投影规律
(2)定比性 :点K在直线AB上,则有:
AK∶KB=ak∶kb=a′k′∶k′b′=a″k″∶k″b″。反之,若点ak∶kb=a′k′∶k′b′=a″k″∶k″b″,则点K在直线AB上。
利用上述两个投影特性,可求出直线上点的投影或判断点是否在直线上。
【例2-4】 如图2-24所示,已知AB上一点C的V面投影c′,求H面投影C。
【解】 过a作一条射线,在射线上截取ac1=a′c′,c1b1=c′b′,连接bb1,过c1作bb1的平行线,交ab于c。由cc1//bb1,可得ac∶ac1=cb∶c1b1,又因为ac1=a′c′,c1b1=c′b′,则ac∶a′c′=cb∶c′b′,因此c即为所求。作图见图2-24。
【例2-5】 如图2-25(a)所示,判断点K是否在侧平线AB上。
【解】 方法一:利用从属性
如图2-25(b)所示,由直线AB和K点的两面投影,补出侧面投影a″b″、k″。因为k″不在a″b″上,所以K点不在直线AB上。
方法二:利用定比性
如图2-25(c)所示,过a′作一条射线,在射线上截取ak1=ak,k1b1=kb,分别连接b′b1 与k′k1。由图可知k′k1不平行于b′b1,所以K点不在直线AB上。

图2-24 利用定比性求直线上点的投影
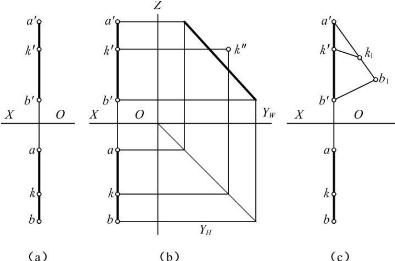
图2-25 判断K点是否在直线AB上
5)两直线的相对位置
空间两直线的相对位置有3种情况:平行、相交和交叉。在相交和交叉中又有垂直相交和垂直交叉的特殊情况。
(1)两直线平行
若两直线在空间相互平行 ,则它们的同面投影除了积聚和重影外仍然相互平行 。如图2-26所示,直线AB和直线CD为一般位置直线,且AB//CD,则ab//cd、a′b′//c′d′、a″b″//c″d″。

图2-26 两直线平行
注意:若两直线是某一投影面的平行线,则必须是两直线在该投影面上的投影相互平行,两直线在空间才相互平行,不能仅根据其他两个投影而直接判别。
【例2-6】 如图2-27(a)、(c)所示,已知两侧平线AB和CD、EF和GH的V、H投影都是平行的,判断空间AB和CD、EF和GH是否平行。
【解】 方法一 作第三投影,如图2-27(b)、2-27(d)所示。可以看出,AB和CD是平行的,而EF和GH是不平行的。
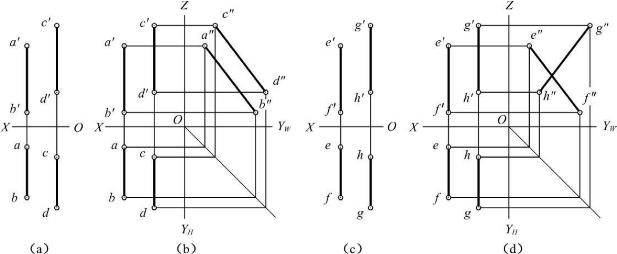
图2-27 判断两直线是否平行
方法二 指向判别
仔细分析可以发现,AB和CD的V、H投影字母顺序是一致的,而且长度也是相等的,说明AB和CD的指向是完全一致的,当然是平行的;而EF和GH的V、H投影字母顺序是相反的,说明它们的指向是不一致的,所以空间也是不平行的。
若两直线是某一投影面的垂直线,则两直线必在空间相互平行。
(2)两直线相交
两直线在空间相交,则它们的同面投影仍然相交,且交点满足投影规律 。如图2-28所示,直线AB和直线CD相交于点K,则有ab与cd相交于k,a′b′与c′d′相交于k′,且kk′⊥OX,满足点的投影规律。

图2-28 两直线相交
注意:若两直线中有某一投影面的平行线时,那么在不反映实长的两个投影面上的投影可能是相交的,但是不能据此评定两直线在空间也是相交的。如图2-29所示,AB与EF都是侧平线,它们在H面和V面的投影中分别与CD和GH相交,但是从W面投影可知EF和GH是不相交的。当然,也可不作W面投影,而根据定比性判断它们是否相交,请读者自己分析。
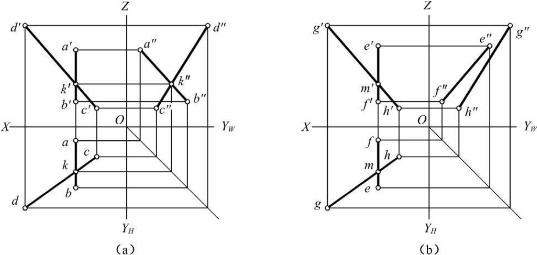
图2-29 判断两直线是否相交
(3)两直线交叉
两直线在空间既不平行也不相交,则称两直线交叉,又称作异面直线。两直线交叉,其同面投影可能有平行的,但三面投影不可能都平行;其同面投影也可能都是相交的,但交点不满足点的投影规律,如图2-30所示。
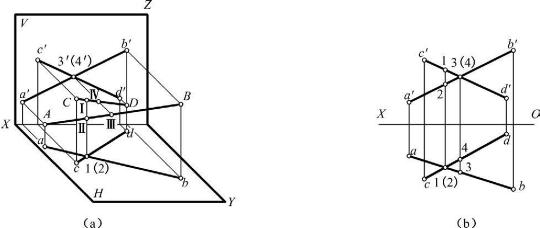
图2-30 两直线交叉
两直线交叉,其同面投影的交点为该投影面重影点的投影,可根据其他投影判别其可见性。如Ⅰ、Ⅱ点为H面的重影点,通过V面投影可知Ⅰ点在上,Ⅱ点在下,因此1点可见,2点不可见;Ⅲ、Ⅳ点为V面的重影点,通过H面投影可知Ⅲ点在前,Ⅳ点在后,因此3点可见,4点不可见。
(4)两直线垂直
若两直线所成夹角为直角,则称两直线垂直,可分为相交垂直和交叉垂直两种情况。垂直两直线的投影特性 :若空间两直线垂直 ,且有一条线平行于某一投影面,那么在该投影面上的投影仍然反映直角 。该特性称为“直角投影定理 ”。
如图2-31所示,已知AB⊥BC,AB∥H。直角投影定理证明如下:
①由AB∥H,Bb⊥H,则AB⊥Bb。
②由AB⊥BC,AB⊥Bb,可得AB⊥平面BCcb。
③由AB∥H,则AB∥ab。

图2-31 直角投影定理
④由AB∥ab,AB⊥平面BCcb,可得ab⊥平面BCcb,则ab⊥bc。根据证明可知,直角定理的逆定理也是成立的:若相交两直线的同面投影反映直角 ,且有一条
直线平行于该投影面,则两直线必垂直 。【例2-7】 如图2-32(a)所示,已知直线AB和点C的两面投影,求C点到AB的距离。
【解】 过C点作CD⊥AB,D点为垂足,则CD的实长即为所求距离。由于AB为正平线,根据直角投影定理可知AB和CD的V面投影反映垂直关系。作图如下:
①过c′作a′b′的垂线,交a′b′于d′。
②过d′作投影连线交ab于d,则求得CD⊥AB。
③采用直角三角形法求CD的实长。如图2-32(b)所示。

图2-32 求点到直线的距离
【例2-8】 求交叉直线AB和CD的距离MN实长及其投影,如图2-33(a)所示。
【解】 两直线的距离即垂直距离,AB和CD的距离MN即为AB和CD的公垂线。由于AB为铅垂线,则MN为水平线。根据直角投影定理,MN和CD的H面投影反映直角,MN的实长为所求距离。
①过ab(m)作cd的垂线,交cd于n,mn即为MN的实长,如图2-33(b)所示。
②过n作投影连线交c′d′于n′,过n′作水平线,交a′b′于m′,如图2-33(b)所示。
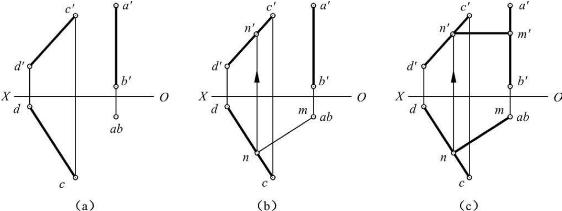
图2-33 求交叉直线的公垂线
2.4.3 平面的投影
1)平面的表示方法
平面的表示方法有两种,一种是用几何元素表示平面,另一种是用迹线表示平面。
(1)几何元素表示法
①不在同一直线上的三点,如图2-34(a)所示。
②一直线和直线外一点,如图2-34(b)所示。
③相交两直线,如图2-34(c)所示。
④平行两直线,如图2-34(d)所示。
⑤任意平面图形,如三角形、四边形、圆形等,如图2-34(e)所示。

图2-34 用几何元素表示平面
(2)迹线表示法
如图2-35(a)所示,平面P与H、V、W三个投影面相交,平面P与H面的交线称为水平迹线 ,用PH表示;平面P与V面的交线称为正面迹线 ,用PV表示;平面P与W面的交线称为侧面迹线,用PW表示。显然,3条迹线中任意两条可以唯一确定平面P的空间位置。
迹线表示法常用于特殊位置平面,如图2-35(b)、(c)所示,而且往往只用有积聚性投影的迹线表示,其他迹线可以省略。

图2-35 用迹线表示平面
2)各种位置平面的投影特性
根据平面对投影面的相对位置的不同,可将平面分成3种:投影面平行面、投影面垂直面和一般位置平面。下面依次介绍每一种平面的投影特性。
(1)投影面平行面
投影面平行面是指与某一个投影面平行的平面,它又可以分为3种:水平面——平行于H面而垂直于V、W面;正平面 ——平行于V面而垂直于H、W面;侧平面 ——平行于W面而垂直于H、V面。
投影特性:投影面平行面 ,在所平行的投影面上的投影反映实形 ;它的另外两个投影积聚成直线 ,且垂直于相关的投影轴 。如表2-4所示。
表2-4 投影面平行面的投影特性

(2)投影面垂直面
投影面垂直面是指与某一个投影面垂直,且与另外两个投影面倾斜的平面,它又可以分为3种:铅垂面 ——垂直于H面而倾斜于V、W面;正垂面 ——垂直于V面而倾斜于H、W面;侧垂面 ——垂直于W面而倾斜于H、V面。
投影特性:在所垂直的投影面上的投影积聚成一条直线 ,该直线与相应投影轴的夹角反映了平面与投影面的倾角 ;另两个投影与空间平面具有类似性 。如表2-5所示。
表2-5 投影面垂直面的投影特性

(3)一般位置平面
一般位置平面是指与3个投影面都倾斜的平面,如图2-36所示。3个投影都不反映空间平面的实形,且投影均不具有积聚性,投影也不反映平面对投影面的倾角的大小,三面投影都具有类似性 。
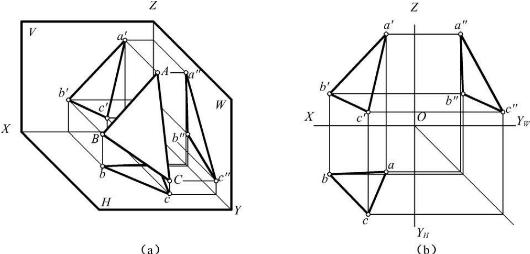
图2-36 一般位置平面的投影
3)平面上的点和直线
(1)若点在平面内的一条直线上 ,则点在该平面上 。如图2-37(a)所示,点M、N分别在直线AC和AB上,则点M、N在平面ABC上。根据这一投影特性可知,若要在平面上作点,必须确定平面上的点所在的直线。
(2)若直线在平面上,则:
①必通过平面上的两个点 。如图2-37(a)所示,直线MN通过平面上的两个点M和N,所以直线MN在平面上。
②过一个点并平行于面上的一条直线 。如图2-37(b)所示,直线ME过平面上的一点M,且平行于平面上的直线AB,所以直线MN在平面ABC上。

图2-37 平面上的点和直线
【例2-9】 已知平面ABC的两面投影及直线EF的水平投影ef,如图2-38(a)所示。直线EF在平面ABC上,求作EF的V面投影。
【解】 因为直线EF在平面ABC上,且EF∥BC(ef∥bc),因此:
①连接a、e得直线ae,与bc相交于点1。过点1向上引投影连线与b′c′相交于点1′,连接a′1′;过点e向上引投影连线,与直线a′1′的交点即为E点的V面投影e′。
②过e′作e′f′∥b′c′。如图2-38(b)所示。

图2-38 求作平面上点的投影
【例2-10】 已知平面图形ABCDEFG的V面投影及直线AB和CD的水平投影,如图2-39(a)所示。试完成其H面投影。

图2-39 完成平面图形的投影
【解】 该平面图形对V、H面都倾斜,所以其H投影与V面投影应该是“类似图形”,因此,按如下方法作图:
①连接d′f′,知道平面图形的外轮廓是平行四边形,则其H投影也应该是平行四边形,分别过a、c作bc和ab的平行线,得四边形abcg。
②按“长对正”在cg边上直接确定d和f。
③延长e′f′交a′b′于1′,同理作出1。
④连接1f,从而确定e。
⑤连接c、d、e、f、g、a,并加粗图形,完成全图。如图2-39(b)所示。
2.4.4 直线与平面、平面与平面的相对位置
直线与平面、平面与平面的相对位置可分为平行、相交和垂直3种情况。
1)平行问题
(1)直线和平面平行
若平面外一直线平行于平面内任一直线,则该直线和平面互相平行 。如图2-40所示,直线AB和平面P内的直线CD平行,则直线AB∥平面P。
【例2-11】 如图2-41(a)所示,已知△ABC和M点,作过M点的水平线MN∥△ABC。
【解】 因所作MN为水平线且要求与△ABC平行,故MN必平行于△ABC内的水平线。作图如下:
①在△ABC内任作水平线AD,其在H和V上的投影为ad和a′d′。
②作MN∥AD,即mn∥ad,m′n′∥a′d′,如图2-41(b)所示。
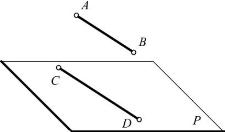
图2-40 直线和平面平行

图2-41 过点作水平线平行于已知平面
【例2-12】 如图2-42所示,判断直线MN与平面ABCD是否平行。
【解】 在平面ABCD内任作一直线EF,使e′f′∥m′n′;作出ef,因ef不平行于mn,所以直线MN不平行于平面ABCD。
当平面的某一投影具有积聚性时,则该投影可反映平面和直线的平行关系。如图2-43所示,平面P是正垂面,a′b′∥P′。故AB∥P。
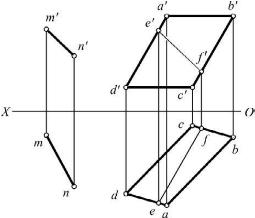
图2-42 判断线面是否平行

图2-43 直线与正垂面平行
(2)平面和平面平行
若两平面内分别有一对相交直线对应平行,则两平面互相平行。如图2-44所示,平面P内的两条相交直线AB和BC分别平行于平面Q内的两条相交直线DE和EF,则平面P∥平面Q。
【例2-13】 如图2-45(a)所示,已知△ABC和M点,过M点作平面平行于△ABC。
【解】 若过M点作两条相交直线分别与△ABC平面内的两条相交直线平行,则由这两条相交直线所确定的平面必平行于△ABC。作图如下:
①作ME∥AB,即me∥ab,m′e′∥a′b′。
②作MF∥AC,即mf∥ac,m′f′∥a′c′。故平面(ME×MF)∥△ABC。如图2-45(b)所示。
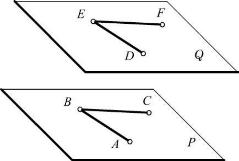
图2-44 两平面平行的几何条件

图2-45 作平面平行于已知平面
【例2-14】 如图2-46所示,判断△ABC和平面DEFG是否平行。
【解】 欲判断两平面是否平行,只要看在一平面内能否作出一对相交直线平行于另一个平面内的两条相交直线。作图如下:
①在平面DEFG内作EM和EN,使e′m′∥a′c′,e′n′∥a′b′。
②作em和en,因为em∥ac,en∥ab,故平面DEFG∥△ABC。
当两平面均垂直于某投影面时,它们有积聚性的投影可直接反映平行关系。如图2-47所示,两铅垂面P和Q的H面投影p∥q,则P∥Q。

图2-46 判断两平面是否平行

图2-47 两铅垂面平行
2)相交问题
相交的问题就是共有的问题,直线和平面的交点是直线和平面的共有点;平面和平面的交线是两平面的共有线。求相交的问题要充分利用积聚性。
在投影图中,通常假设平面是不透明的,当直线和平面以及平面和平面相交而发生互相遮挡,应根据“上遮下、前遮后 、左遮右 ”的原理判断两者的可见性,并用实线表示可见部分,虚线表示不可见部分。
(1)一般位置直线和特殊位置平面相交
若平面处于特殊位置,其某一投影具有积聚性,则直线与平面的交点可利用直线与平面的积聚性投影相交而直接求得。
【例2-15】 如图2-48(a)所示,一般位置直线AB与铅垂面P相交,求作交点K。
【解】 由于交点K既在AB上,又在平面P内,且平面P在H上投影为一直线,故该直线与AB的交点K即为所求。作图如下:
①确定直线AB与平面P在H上的交点k。
②过k点作ox轴的垂线,与a′b′交于k′。
③根据H面投影判断,KA段在平面P之前,其V面可见,a′k′投影为实线;KB段在P面之后,k′b′有部分被遮挡不可见,投影为虚线,如图2-48(b)所示。

图2-48 作一般位置直线与铅垂面的交点
(2)投影面垂直线和一般位置平面相交
【例2-16】 如图2-49(a)所示,正垂线MN与一般位置平面△ABC相交,求作交点K。
【解】 由于交点K既在MN上,又在平面△ABC内,且MN在V上投影为一点,故该点即为MN与平面△ABC的交点K在V上的投影k′。作图如图2-49(b)所示。
根据交叉两直线的重影点判断可见性:mn和ac的交点1(2),是MN上Ⅰ点和AC上Ⅱ点的重影点,由V面投影可知,Ⅰ点在Ⅱ点之上,故NK段可见,nk投影为实线;KM段有部分不可见,其H投影km在△abc内的部分为虚线。
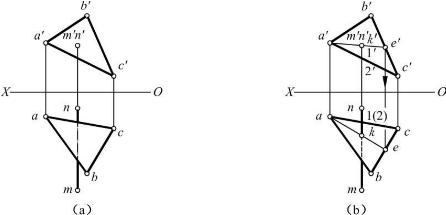
图2-49 作正垂线与一般位置平面的交点
(3)两特殊位置平面相交
两平面相交,且均垂直于某一投影面,其交线必垂直于该投影面。则两平面的交线可利用平面的积聚性投影求得。
【例2-17】 如图2-50(a)所示,水平面Q与正垂面P相交,求作交线KL。
【解】 由于水平面Q⊥V,正垂面P⊥V,则交线KL⊥V,故在V上投影积聚成一点,即为水平面Q和正垂面P在V上的投影之交点k′l′。其H投影kl⊥OX。
根据平面的积聚性投影判断,交线左侧水平面Q在上为可见,右侧正垂面P在上为可见。即在H上,kl左侧水平面Q投影画实线,kl右侧正垂面P投影画实线。

图2-50 作水平面与正垂面的交线
(4)一般位置平面与特殊位置平面相交
【例2-18】 如图2-51(a)所示,求作一般位置平面△ABC与铅垂面Q的交线KM。
【解】 由于铅垂面Q⊥H,故交线KL在H上的投影kl与Q重合。k′和l′分别在a′b′和a′c′上。根据H面投影判断,△ABC的akl部分在平面Q之前,所以,a′k′l′是可见的,画实线,另一部分不可见,画虚线,如图2-51(b)所示。

图2-51 作铅垂面与一般位置平面的交线
(5)一般位置直线和一般位置平面相交
若直线和平面均处于一般位置,则两者的投影均无积聚性,所以,交点的投影无法直接从投影图中得到,可采用辅助平面法求作,把问题转换为上述情况。其作图步骤如下:
①包含一般位置直线作一辅助平面,通常作投影面的垂直面。
②作辅助平面和一般位置平面的交线。
③求作此交线和一般位置直线的交点。
【例2-19】 如图2-52(a)所示,一般位置直线MN和一般位置平面△ABC相交,求作交点K,并判别可见性。
【解】 根据上述分析,作图如下:
①包含MN作辅助铅垂面Q,其H投影QH与mn重合,如图2-52(b)所示。

图2-52 作一般位置直线与一般位置平面的交点
②确定QH和△ABC的交线ef,即为Q平面与△ABC的交线EF的H投影。
③作出e′f′,与直线m′n′相交于k′。即为所求交点K的V面投影。
④根据各投影面上的重影点判断可见性。在H投影中,ab和mn的交点e(1),由V面投影可知,E点在Ⅰ点之上,故k1段不可见,应画虚线,另一段k′n′则画实线。在V投影中,b′c′和m′n′的交点2′(3′),由H面投影可知,Ⅱ点在Ⅲ点之前,故k′2′段可见,应画实线,另一段画虚线。
可见性判别有一个技巧:如果平面的两面投影的顺序一致(如a′b′c′和abc都是顺时针),那么直线的两面投影的可见性也一致,即同一段的两面投影要么都可见,要么都不可见(如k′n′和kn都可见,k′m′和km都不可见);同理,如果平面的V、H投影的顺序不一致,那么直线的两面投影的可见性刚好相反。请读者自己验证。
(6)两个一般位置平面相交
两个一般位置平面的交线可采用直线与平面求交点的方法求得。取一平面内的任意两条直线,作出它们与另一平面的交点,则交点一定是两平面交线上的点,连接两交点得两平面的交线。这里不作要求。
3)垂直问题
(1)直线与平面垂直
若直线垂直于平面内的两相交直线 ,则该直线与平面垂直 。反之 ,若直线与平面垂直 ,则该直线垂直于平面内的所有直线 。如图2-53所示,直线MN垂直于平面P内的相交直线AB和CD,则直线MN⊥平面P。反之,若直线MN垂直于平面P,则直线MN垂直于平面P内的任意直线,即MN⊥EF,MN⊥KL。
由上可知,直线与平面垂直的问题可转化为两直线垂直的问题。
如图2-54所示,直线MN⊥平面P,必垂直于平面P内的水平线AB和正平线AC。由直角定理可知,在投影图中,mn⊥ab,m′n′⊥a′c′。

图2-53 直线与平面垂直的几何条件

2-54 直线与平面垂直的投影特性
因此,直线与平面垂直的投影特性为 :
直线的H·面投影与平面内水平线的H ·面投影垂直;直线的V·面投影与平面内正平线的V·面投影垂直 ;直线的W·面投影与平面内侧平线的W·面投影垂直 。
【例2-20】 如图2-55(a)所示,已知ABCD为矩形,试完成其投影。
【解】 矩形的邻边相互垂直,所以空间AB和BC是垂直的。由于AB是一般位置直线,所以不能直接利用直角投影定理作出BC的H投影。但是BC肯定位于过B点且与AB垂直的平面内,因此,可以这样作图:
①过B点作一对相交直线BⅠ×BⅡ分别垂直于AB。其中:BⅠ为正平线,b′1′⊥a′b′;BⅡ为水平线,b2⊥ab。则BC一定位于BⅠ×BⅡ所确定的平面上。在此平面上作辅助线ⅠC(1′c′)交BⅡ于点E(e、e′),如图2-55(b)所示。
②C在ⅠE的延长线上,所以延伸1e交cc′的投影连线于c,再根据平行四边形的投影特性作出d,并加粗轮廓线。如图2-55(c)所示。

图2-55 完成矩形的投影
【例2-21】 如图2-56(a)所示,求点A到直线BC的距离L。
【解】 所说距离当然是垂直距离,即过A点向BC所作垂线的长度。由于BC是一般位置直线,所以这样的垂线不能直接作出。在空间过A点作直线与BC垂直可以有无数条,它们组成一个平面,但是垂直相交的只有一条,即A点和BC与垂面交点的连线,因此按如下思路作图:
①过A点作一对相交直线AⅠ×AⅡ分别垂直于BC。其中:AⅠ为水平线,a1⊥bc;AⅡ为正平线,a′2′⊥b′c′,如图2-56(b)所示。
②包含直线BC(b′c′)作辅助面PV,求PV与所作垂面的交线ⅠⅡ(1′2′、12),继而求出直线BC与所作垂面的交点D(d、d′),如图2-56(c)所示。
③连接ad、a′d′即为距离的两面投影,再用直角三角形法求其实长L,如图2-56(d)所示。
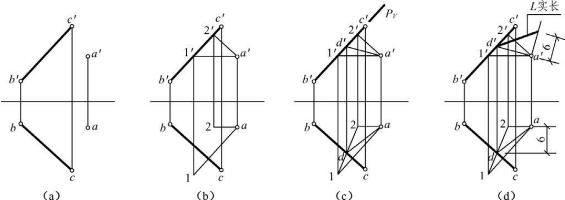
图2-56 求点到直线的距离
4)平面与平面垂直
若直线垂直于平面 ,则包含此直线的所有平面均和该平面垂直 。反之 ,若两平面互相垂直 ,过其中一平面内任一点作另一平面的垂线 ,则垂线必在该平面内 。如图2-57所示,直线MN垂直于平面P,则过直线MN的平面Q和R均垂直于平面P。反之,若平面Q⊥平面P,过平面Q内的M点作MN⊥平面P,则直线MN在平面Q内,如图2-58所示。

图2-57 平面与平面垂直的几何条件

图2-58 判断两平面是否垂直
【例2-22】 如图2-59(a)所示,过直线MN求作一平面垂直于△ABC。
【解】 因为AB和AC分别是△ABC内的水平线和正平线,所以,作直线ml⊥ab,m′l′⊥a′c′,则ML⊥△ABC。所以,由直线MN、ML确定的平面垂直于△ABC,如图2-59(b)所示。

图2-59 作已知平面的垂直面
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















