3 基本体的投影
所谓基本体,就是简单的几何形体,包括棱柱、棱锥、棱台等平面立体和常见的圆柱、圆锥、圆球和圆环等回转体以及常见的工程曲面。这里主要研究这些基本体的投影特点及其表面上取点、线的问题,还有平面和立体相交的问题。
3.1 平面立体的投影
平面立体也称多面体,它的表面都是由平面围成的,常见的简单的平面体有棱柱、棱锥和棱台,它们的投影各有特点,分述如下。
3.1.1 棱柱体
棱柱体的特点是有一组相互平行的棱线和两个平行的底面。当底面与棱线垂直时称为直棱柱,底面各边相等的直棱柱称为正棱柱。工程上常见的棱柱为直棱柱或正棱柱,且往往处于特殊位置,即棱线垂直于投影面。
图3-1(a)所示为一棱线垂直于H面的正五棱柱,按点、线、面的投影规律,作出其三面投影如图3-1(b)所示。五棱柱的上、下底为水平面,所以其H投影重合为反映实形的正五边形,五边形的各边分别是五棱柱各个侧面的积聚投影,5个顶点则是各棱线的积聚投影;V面投影的外框为矩形,矩形的上、下两条边分别是五棱柱上、下底面的积聚投影,3条可见的铅直线分别是左、前、右棱线的实长投影,构成的两个可见矩形则是左前、右前两个侧面的类似形投影,两条虚线是后方不可见棱线的投影;W面投影的外框也是矩形,上、下两条边同样是五棱柱上、下底面的积聚投影,3条可见的铅直线分别是左后、左前和后棱线的实长投影,构成的两个矩形则分别是左后、左前侧面的类似形投影。
从图3-1(b)可以看出:两个投影的外框是矩形,另一个投影反映形状特征。对于其他处于特殊位置的直棱柱同样有这样的投影特点,所以可概括为“矩、矩为柱”。
【例3-1】 如图3-2(a)所示,已知五棱柱表面上的一个点A和一条线BC的一个投影,求作它们的其他两面投影。
【解】 在平面立体表面上取点、线,实际上就是在各侧表面——平面上取点、线,与单纯地在平面上取点、线稍有区别的是有可见性判别的问题。
分析和作图如图3-2(b)所示。
①作A点的投影
从a′的位置和可见性可以判别,A点位于五棱柱的右前方侧表面上,先利用积聚性作出其H投影a,然后再作出其W投影(a″),不可见。
②作直线BC的投影
由b″c″的位置及可见性可以判别,直线BC位于五棱柱的左后方侧表面上,先利用积聚性作出其H投影bc,然后再作出其V投影(b′)(c′),不可见,画为虚线。

图3-1 正五棱柱的投影

图3-2 棱柱体表面上的点和线
3.1.2 棱锥体
棱锥体的特点是有一个底面,其他各侧面的交线相交于一个顶点。
图3-3(a)所示是一个三棱锥,三棱锥的底面平行于H面,其他3个侧面均为一般位置平面,其投影如图3-3(b)所示。底面的H投影反映实形,V、W投影积聚为水平线,3个侧面的三面投影均为类似图形。注意棱线SC的侧面投影不可见,所以表示为虚线。

图3-3 三棱锥的投影
对于底面投影有积聚性的锥体,其三面投影中至少有两个投影的外框是三角形,所以其投影特点可概括为“三、三为锥 ”。
【例3-2】 如图3-4(a)所示,已知三棱锥表面上的一个点E和一线段MN的一个投影,求作它们的其他两面投影。
【解】 分析和作图如图3-4(b)所示。
①作E点的投影
由(e′)的位置及其不可见性可以知道,E点位于三棱锥的SAC棱面。过E点在SAC棱面作辅助线SⅠ(s′1′),交底边AC于Ⅰ点(1′),再作出SⅠ的H投影s1,因为E点在SⅠ上,从而得到e在s1上,最后根据e和(e′)作出(e″),不可见。

图3-4 棱锥体表面的点和线
②作线段MN的投影
根据m′n′的位置和可见性可以判别,M点位于三棱锥的SAB棱面上,N点位于三棱锥的SBC棱面上,MN横跨了两个棱面,所以MN在空间不是一个直线段,而是多了一个转折点的折线段,转折点K位于棱线SB上。先由k′作出k″,从而确定k。
过M点(m′)在SAB(s′a′b′)上作辅助线SⅡ(s′2′),交底边AB(a′b′)于Ⅱ(2′),再作出辅助线SⅡ的H投影s2,继而确定m和m″。
过N点(n′)在SBC(s′b′c′)上作辅助线NⅢ(n′3′)∥底边BC(b′c′),交棱线BC(b′c′)于Ⅲ(3′),再作出辅助线NⅢ的H投影n3,继而确定n和(n″)。
连接mk、kn和m″k″、k″(n″),因为棱面SBC的W投影(s″b″c″)不可见,所以k″(n″)不可见,画为虚线。
3.1.3 棱台体
棱台的特点是有两个平行且相似的底面,对应顶点的连线延长后交于一点。实际上就是将棱锥平切去一个头,所以其投影特点可概括为“梯、梯为台”(图略)。
3.2 平面立体截交线
平面与立体相交,就是假想用平面去截切立体,此平面称为截平面 ,所得表面交线称为“截交线 ”。一般来说,截交线是闭合的图形。
平面体的表面都是由平面组成的,所以平面体的截交线一般是闭合的平面多边形,多边形的各边就是截平面与平面体各个表面的交线,各个顶点就是截平面与平面体各个棱线的交点。求平面体截交线的方法有如下几种:
(1)线—面交点法 。就是通过求截平面与平面体的各棱线的交点,即平面多边形的各个顶点,然后把相邻两点(即位于同一棱面上的两点)连成线。
(2)面—面交线法 。就是直接求作截平面与平面体各棱面的交线。
(3)积聚性法。由于截平面一般都处于特殊位置,至少有一个投影具有积聚性,这样就可以把求平面体截交线的问题转化为在平面体各个表面——也就是平面上取点、线来解决。这里主要介绍这种方法。
【例3-3】 如图3-5(a)所示,求带切口三棱锥的H、W投影。
【解】 从V面投影可以看出,该切口由一个水平面和一个正垂面构成,它涉及了三棱锥的3个侧表面。完整的三棱锥的3个侧表面分别为:△SAB和△SBC都是一般位置平面,其三面投影应均为类似图形;△SAC为侧垂面,其V、H投影应该为类似图形。它们被开了切口以后,形状发生了变化,但是位置没有变化,因此投影的特性不会发生变化。这样就可以通过对投影特性的分析,再利用平面上取点、线的方法迅速解决其余两面投影。
具体来说,△SAB被开了切口以后变成一个△SⅣⅤ(s′4′5′)和四边形ⅠⅡ或AB(1′2′b′a′),其H、W投影应该是与其相类似的图形s45和s″4″5″及12ab和1″2″a″b″;△SBC被开了切口以后变成一个六边形SⅣⅢⅡBC(s′4′3′2′b′c′),其H、W投影应该是与其相类似的图形s432bc和s″4″3″2″b″c″;△SAC被开了切口以后变成一个六边形SⅤⅥⅠAC,其H投影应该是与其相类似的图形s561ac,W投影积聚为一直线。最后再分析由两个截平面相交而产生的交线ⅢⅥ及其投影的可见性并处理轮廓线。
具体的作图过程如图3-5(b)的箭头所示。

图3-5 切口三棱锥的投影
这里一定要注意:在作图之前,必须对立体各个表面的空间位置和被截平面截切前后的形状变化及其投影应该有什么样的特点进行分析,初学时还要学会对各个顶点进行编号,这样就可以明晰作图的思路,并对作图结果有一个准确的形状(类似图形)意识,最后即使不检验作图的过程也能一目了然的判断作图结果的正确与否。
【例3-4】 补全如图3-6(a)所示形体的V、H投影。
【解】 首先进行形体分析:根据投影特点,可以知道这是一个四棱柱,在其中前方被从左到右开通了一个切口,切口由两个侧垂面和一个正平面构成。开了切口以后,形体的左右依然是对称的。作图结果如图3-6(b)所示。
投影分析:四棱柱的4个侧表面都是铅垂面,所以其V、W投影应为类似图形。从W投影可以看出,左前方侧表面由矩形ABB1A1变成了四边形ABⅠⅡ(a″b″1″2″)和ⅤⅥB1A1 (5″6″b″1a″1),其V面投影应该是与其相类似的图形(a′b′1′2′)和(5′6′b′1a′1);左后方侧表面由矩形ADD1A1变成了八边形AⅡⅢⅣⅤA1D1D(a″2″3″4″5″a″1d″1d″),其V面投影应该是与其相类似的图形(a′2′3′4′5′a′1d′1d′);由于形体是左右对称的,相应的作出其右前方和右后方的投影;最后再分析由3个截平面产生的两条交线——侧垂线,并判别可见性和处理轮廓线。

图3-6 补全四棱柱的投影
3.3 平面立体相贯线
两个立体相交又称为两个立体相贯 ,其表面交线称为“相贯线 ”。相贯线一般是闭合的空间图形,而且为两个立体表面所共有。当一个立体全部穿过另一个立体时,称为全贯 ,相贯线有两组,如图3-7(a)所示;当两个立体都只有部分参与相交时,称为互贯,相贯线只有一组,如图3-7(b)所示。
两个平面立体的相贯线一般情况下为空间多边形(折线),特殊情况下是平面多边形。实际上也就是一个立体的各个表面与另一个立体表面的截交线的组合。因此,求相贯线的问题完全可以转化为求截交线的问题,方法同求截交线一样。这里仍然重点介绍积聚性法。

图3-7 两个立体相交
【例3-5】 求作图3-8(a)所示两立体的相贯线。
【解】 形体分析:这是两个棱线分别垂直于H、W的三棱柱产生相贯,横向的三棱柱完全穿过直立的三棱柱,所以是全贯。相贯线分左、右两组:左边的一组实际上就是由直立的三棱柱的两个侧面DE和DF分别与横向三棱柱的截交线组成;右边的一组就是直立的三棱柱的右侧面EF与横向三棱柱的截交线。
投影分析:由于两个三棱柱的H、W面投影分别具有积聚性,所以只需要求相贯线的V面投影。因为直立三棱柱的3个侧面都是铅垂面,所以其V面投影和W面投影应为类似图形。它们被横向的三棱柱相贯以后,从W面投影看表面发生了如下变化:左后侧面DF多了Ⅰ-Ⅱ-Ⅲ(1″-2″-3″)3个转折点,对应的图形由矩形变成了七边形;左前侧面DE多了Ⅲ-Ⅳ-Ⅴ-Ⅰ(3″-4″-5″-1″)4个转折点,对应的图形由矩形变成了八边形;右前侧面EF的外框没有变,里面多了一个三角形Ⅵ-Ⅶ-Ⅷ(6″-7″-8″)。
作图过程如图3-8(b)所示。
①作出各个转折点对应的V面投影。
②依次连接各点成相贯线。这里注意连点的顺序必须和W面投影一致,遵循:同一平面上的两个点可以连,如Ⅰ-Ⅱ、Ⅱ-Ⅲ等;同一棱线上的两个点不能连,如Ⅰ-Ⅲ、Ⅱ-Ⅶ、Ⅳ-Ⅷ等。同时,注意各个侧面类似图形的分析,用形象思维确保作图的正确性。
③判别可见性。Ⅰ-Ⅱ、Ⅱ-Ⅲ是直立三棱柱后侧面上的线段,所以其V面投影1″-2″-3″不可见;Ⅴ-Ⅰ和Ⅵ-Ⅶ是横向三棱柱后侧面上的线段,所以其V面投影5″-1″和6″-7″不可见。这里就发现一个可见性的判别原则是:只有两个面的投影都可见时,其交线的投影才可见,只要有一个面的投影是不可见的,那么其交线的投影亦不可见。
④处理轮廓线。参与相交的各棱线需连接到相应的转折点,并且按可见性画为实线和虚线,同一棱线上的两个转折点之间已和另一立体融为一体,没有线。没有参与相交的棱线也应按其可见性处理为实线或虚线,如F棱线没有参加相贯,其被横向三棱柱遮挡住的部分应画为虚线,未被遮挡住的部分应画为实线。

图3-8 求作两个立体的相贯线(全贯)
【例3-6】 求作图3-9(a)所示两立体的相贯线。
【解】 形体分析:这是一个棱线垂直于V面的三棱柱和一个三棱锥相贯,三棱柱只有两个侧面参与相交,所以是互贯,相贯线只有一组,实际上就是三棱柱的两个侧面LM和MN与三棱锥相交的截交线,所以此题和图3-5类似,所不同的是图3-5是空体(切口)相交,这里是实体相交。
投影分析与作图:由于三棱柱的V面投影具有积聚性,所以相贯线为已知:Ⅰ-Ⅱ-Ⅲ-Ⅳ-Ⅴ-Ⅵ(1″-2″-3″-4″-5″-6″)。又根据相贯线是共有的原则,它也在三棱锥表面上,这样就把求相贯线的问题转化为在三棱锥表面——平面上取点、线来解决,分析同例3-3,这里不重复讲述(读者可对三棱锥进行编号后自己分析)。所不同的是这里的三棱柱是实体,因此:在其下底面MN上的线段Ⅰ-Ⅱ、Ⅱ-Ⅲ和Ⅰ-Ⅵ的H投影1-2、2-3和1-6是不可见的;在其右侧面LM上的线段Ⅲ-Ⅳ、Ⅳ-Ⅴ和Ⅴ-Ⅵ的W投影3″-4″、4″-5″和5″-6″是不可见的;另外,两个实体相贯的部分被认为是融为一体的,所以Ⅲ和Ⅵ之间是不能连线的。最后处理轮廓线,原则同上例。结果如图3-9(b)所示。

图3-9 求作两个立体的相贯线(互贯)
3.4 回转体的投影
常见的回转体有圆柱、圆锥、圆球和圆环等。
3.4.1 圆柱
1)圆柱的形成
如图3-10(a)所示,一矩形平面绕着其中的一条边为轴线旋转一周,便形成了一个圆柱体。按此方式形成的圆柱体是一个包含上、下底的实心圆柱,侧面称为圆柱面,是由与轴线平行的一边旋转而形成的,该边旋转到某一具体位置时称为圆柱面的素线,圆柱面上的素线相互平行。
2)圆柱的投影
图3-10(a)所示为一轴线垂直于H面的铅直圆柱,其三面投影如图3-10(b)所示:H投影为圆柱的上、下底圆的实形投影,圆周则是整个圆柱面的积聚投影;V、W投影均为矩形,矩形的上、下两条边分别是圆柱上、下底圆的积聚投影,另外两条边则分别是最左、最右素线(AA1、BB1)和最前、最后素线(CC1、DD1)的投影(a′a1′、b′b1′和c″c1″、d″d1″)。注意,这样的轮廓线在圆柱表面实际上是不存在的,仅仅是由于投影而产生的,所以也称为投影轮廓线,它们客观上也形成了前、后半柱和左、右半柱的分界线。对应的其他投影只表示了其位置(a″a1″、b″b1″和c′c1′、d′d1′),而没有线的存在。
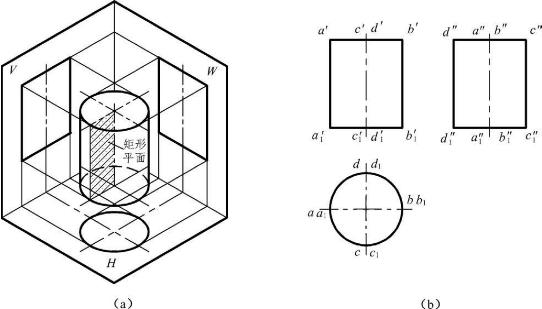
图3-10 圆柱的形成及投影
3)圆柱面上的点
由于圆柱的一个投影具有积聚性,所以在圆柱表面取点可以用积聚性法解决。
【例3-7】 求作图3-11(a)所示圆柱上的点E和F的其他两面投影。
【解】 分析与作图步骤如图3-11(b)所示。
①由(e′)的位置及其不可见性,可知E位于左后方的圆柱面上,其H投影e在左后半圆周上,再根据投影规律由(e′)和e作出e″,可见。
②由f′的位置及其可见性,可知F位于右前方的圆柱面上,其H投影f在右前方的圆周上,再根据投影规律由f′和f作出(f″),不可见。

图3-11 圆柱面上取点
3.4.2 圆锥
1)圆锥的形成
如图3-12(a)所示,一直角三角形绕其一直角边为轴线旋转一周便形成了一个圆锥体。按此方式形成的圆锥是一个包含底圆的实心圆锥,侧面称为圆锥面,它是由三角形的斜边旋转而形成的,该边旋转到某一具体位置时称为圆锥面的素线,锥面上所有的素线相交于锥顶。
2)圆锥的投影
图3-12(b)为一轴线垂直于H面的直立圆锥的三面投影:其H投影为圆锥的下底圆的实形投影,同时也是所有锥面的投影;V、W投影均为三角形,三角形的底边是圆锥下底圆的积聚投影,另外两条边则分别是最左、最右素线(SA、SB)和最前、最后素线(SC、SD)的投影(s′a′、s′b′和s″c″、s″d″)。同样,这样的轮廓线在圆锥表面实际上也是不存在的,仅仅是由于投影而产生的投影轮廓线,它们客观上也形成了前、后半锥和左、右半锥的分界线。对应的其他投影只表示了其位置(s″a″、s″b″和s′c′、s′d′),同样没有线的存在。

图3-12 圆锥的形成及投影
3)圆锥面上的点
由于圆锥面的三面投影均无积聚性,所以在圆锥面上取点一般需用辅助线来作图,常用的方法有素线法和纬圆法。如图3-13(a)所示。
【例3-8】 已知圆锥上M的点V面投影,求作其他两面投影。
【解】 素线法作图步骤如图3-13(b)所示。
①由m′可知,点M在左前方锥面上,过m′作s′n′,再作sn和s″n″。
②根据m′在s′n′上,则分别在sn和s″n″作出m和m″,均可见。
纬圆法作图步骤如图3-13(c)所示:
①过m′作水平线与最左、最右投影轮廓线相交,从而确定纬圆的直径。
②在H投影中作出该纬圆的实形,由m′作出m,继而作出m″,均可见。

图3-13 圆锥面上取点
一般来说,用素线法和纬圆法都可以。但当纬圆的半径较小,圆规不便作图时,可选用素线法;而当点的投影靠近轴线,使得所作素线和轴线的夹角较小时,为提高作图的精度,可选用纬圆法。
3.4.3 圆球
1)圆球的形成
如图3-14(a)所示,一半圆(或圆)绕其直径旋转一周便形成了一个圆球。按此方式形成的圆球当然也是实心的圆球,整个外表面便是球面。
2)圆球的投影
从任何方向观察球面,其效果是一样的,即其三面投影均为直径大小相等的圆,如图3-14(b)所示。同样,球面是光滑的曲面,其上不存在任何轮廓线,其三面投影的大圆b′、a和c″则分别是前、后半球(V面)和上、下半球(H面)及左、右半球(W面)理论上的分界线的投影。它们对应的其他面的投影也是不存在的,图中只表明了它们的理论位置。

图3-14 圆球的形成及投影
3)圆球面上的点
由于圆球面是非直纹曲面,其上不存在直线,所以应该用平行于投影面的纬圆作为辅助线,即用纬圆法作图。注意:如果纬圆的方向不同,对于同一点,它的半径也是不一样的。
【例3-9】 求作图3-15(a)所示圆球上的点D和E的其他两面投影。
【解】 作图步骤如图3-15(b)所示。
①由d′可知,D点位于正平大圆,即前后半球的分界线上,可以直接作出d和(d″)。又因D点位于球的右上方,所以d可见,而(d″)不可见。
②由(e)的位置及可见性可知,E点位于球的左前下方。先过点(e)作水平纬圆,再作出该水平纬圆的V面投影——水平线,其长度就是该圆的直径,继而作出e′和e″,均可见。

图3-15 圆球面上取点
说明:虽然从理论上讲可以作任意方向的纬圆,但为避免初学者画任意方向的直线,容易和素线法混淆,所以建议遇到已知点就画一个纬圆,这样就可以明确该纬圆的性质。当然,如果已知点离球心太近,不便于画圆时,可以考虑作投影面的平行线。
3.4.4 圆环
1)圆环的形成
如图3-16(a)所示,一圆平面绕着与其共面的圆外一直线为轴线旋转一周,便形成了一个圆环面。靠近轴线的半圆CBD旋转形成内环面,远离轴线的半圆DAC旋转形成外环面。圆周上离轴线最远的点A的旋转轨迹称为赤道圆,离轴线最近的点B的旋转轨迹称为颈圆。
2)圆环的投影
图3-16(a)所示为一轴线垂直于H面的圆环,其三面投影如图3-16(b)所示:H投影为两个同心圆,分别是赤道圆和颈圆的投影;V、W面投影为两个大小相等的“鼓形”,鼓的上下两个底面分别是圆平面上最高、最低两个点的运动轨迹圆的积聚投影,V面投影的左、右两个圆是前、后半环的分界线的投影,W面投影前、后两个圆则是左、右半环的分界线的投影。
对于H面投影,上半环面可见,下半环面不可见;对于V面投影,只有前半环的外环面可见,其余均不可见;对于W面投影,只有左半环的外环面可见,其余均不可见。

图3-16 圆环的形成及投影
3)圆环面上的点
和球面一样,环面也是非直纹曲,只能用纬圆法来作图。
【例3-10】 求作图3-17(a)所示圆环上的点E和F的其他两面投影。
【解】 作图步骤如图3-17(b)所示。
①由(e)的位置及其不可见性,可知点E位于左后下方的内半环。先过(e)作水平纬圆,再作该纬圆的V面投影——水平线,长度等于水平纬圆的直径,继而作出(e′),不可见。
②由f′的位置及其可及性,可知点F位于右前上方的外半环。先过f′作水平线,交于环的外轮廓线,即得水平纬圆的直径,按其直径作水平纬圆的H投影,继而作出f,可见。
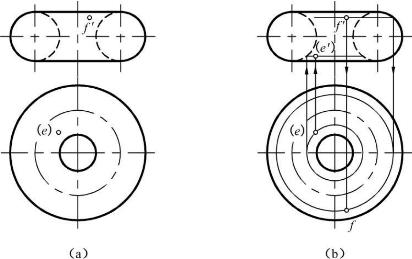
图3-17 环面上取点
3.5 回转体的截交线
回转体的截交线一般情况下是闭合的平面曲线。当截平面与直纹曲面交于直素线,或者与回转体的平面部分相交时,截交线可为直线段。
由于常见的截平面至少有一个投影具有积聚性,因此,根据截交线是共有线的特性,求回转体的截交线问题就可以归结为在回转体表面取点的问题:先求出一系列的共有点,然后再顺次连接成光滑的曲线或直线。为了能准确地作出截交线,首先要求出一些特殊点,如控制截交线范围的最左、最右、最前、最后、最高、最低点,以及控制可见性的各个投影轮廓线上的点(也是截交线和投影轮廓线的切点)等,然后再根据需要作出一些中间点,并最终连成截交线。
回转体截交线投影的可见性与平面体截交线类似,当截交线位于回转体表面的可见部分时,这段截交线的投影是可见的,否则是不可见的。但若回转体被截断后,截交线成了投影轮廓线,那么该段截交线也是可见的(虽然它可能处于回转体的不可见部分,见图3-19的H、W面投影)。
3.5.1 圆柱的截交线
根据截平面与圆柱轴线的相对位置的不同,截交线的形状有3种情况,如表3-1所示。
表3-1 圆柱的截交线

当截平面与圆柱轴线平行时,截交线为矩形(与侧表面的交线为平行两直线);当截平面与圆柱轴线垂直时,截交线为圆;当截平面与圆柱轴线倾斜时,截交线为椭圆,特殊情况下投影为圆(夹角为45°)。
【例3-11】 求作图3-18(a)所示带切口圆柱的其他两面投影。
【解】 该圆柱切口是由一个侧平面、一个水平面和一个正垂面一起切割圆柱而形成的。侧平面与圆柱轴线垂直,切得的截交线为侧平圆弧,其W投影在圆周上,H投影积聚为一直线;水平面与圆柱轴线平行,切得的截交线为矩形,其W投影积聚为一不可见的直线(因为在切口的底部),H投影反映实形;正垂面与圆柱轴线倾斜,切得的截交线为椭圆弧,其W 和H投影为类似图形(分别为圆弧与椭圆弧)。
作图步骤如图3-18(b)所示。
①侧平圆弧的H投影积聚为一直线,可直接作出,其宽即为直径。
②矩形截交线的宽由W投影所积聚的虚线确定,从而确定其H的实形投影。
③椭圆弧的投影则通过确定一系列的点,再由这些点连接成光滑的曲线。首先是特殊点:最左点A和E,也是最低点;最前点B;最后点D;最右点也是最高点C。因为B和C及C和D之间的距离较大,所以分别插入一般点Ⅰ和Ⅱ。作图顺序如图中箭头所示。
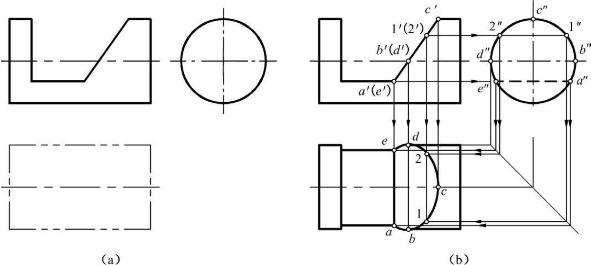
图3-18 求作切口圆柱的投影
3.5.2 圆锥的截交线
根据截平面与圆锥的相对位置的不同,截交线的形状有5种情况,如表3-2所示。
当截平面通过圆锥的锥顶时,截交线为三角形(含锥底的交线,与锥面的交线为两条相交直线);当截平面垂直于圆锥的轴线时,截交线为圆;当截平面倾斜于圆锥的轴线且与所有素线都相交时,截交线为椭圆;当截平面只与圆锥面的一条素线平行时,截交线为“抛物弓形”(含锥底的交线,与锥面的交线为抛物线);当截平面与圆锥的轴线(或两条素线)平行时,截交线为“双曲弓形”(含锥底的交线,与锥面的交线为双曲线)。
表3-2 圆锥的截交线

【例3-12】 求作图3-19(a)所示截头圆锥的其他两面投影。
【解】 这是一个圆锥被一个与圆锥轴线倾斜的正垂面、一个过锥顶的正垂面和一个与圆锥轴线垂直的水平面所截。过锥顶的正垂面所截的截交线是直线,水平面所截的截交线为水平圆弧,它们分别可以用素线法和纬圆法很快确定。与圆锥轴线倾斜的正垂面所截的截交线为椭圆弧,其作图较为繁琐,首先要求出一系列的特殊点,然后再增加一般点,最后再连接成光滑的曲线,其作图步骤如图3-19(b)所示。
①确定最左、最低点Ⅰ;最右、最高点Ⅳ和Ⅴ;最前、最后投影轮廓线上的点Ⅲ和Ⅵ。
②椭圆弧上顶最前、最后点Ⅱ和Ⅶ按如下方法确定:延长正垂面与圆锥的最右轮廓线相交于Ⅷ,则正平线Ⅰ-Ⅷ即为椭圆的长轴,过长轴的中点作水平纬圆,则该纬圆的直径即为短轴的长,短轴为正垂线,水平投影反映实长,短轴的两个端点即是最前、最后点Ⅱ和Ⅶ。
③用纬圆法在点Ⅰ、Ⅱ和Ⅰ、Ⅶ之间分别增加一般点A和B。
④最后依次连接各个点成光滑的曲线,并处理轮廓线。

图3-19 求作截头圆锥的投影
3.5.3 圆球的截交线
无论截平面与球面的相对位置如何,它与球面的截交线总是圆。截平面越靠近球心,截得的圆越大,其最大直径就是球的直径,其时截平面通过圆心。
当截平面与投影面平行时,截交线圆在该面上的投影反映实形,否则其投影为椭圆(特殊情况下积聚成直线)。
【例3-13】 求作图3-20(a)所示带切口圆球的其他两面投影。
【解】 这是由一个侧平面和一个正垂面切去了球的右上方所形成的。侧平面切得的截交线为侧平圆弧,其W投影反映实形,H投影积聚成直线,作图比较简单。正垂面切得的截交线为正垂圆弧,其V投影积聚成直线,H、W投影均为椭圆弧,其作图较为繁琐,如图3-20(b)所示。
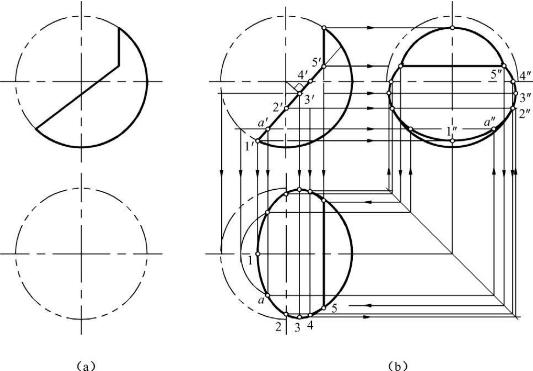
图3-20 求作切口圆球的投影
①先作一系列的控制点:最左点也是最低点Ⅰ在正平大圆上,由1′而确定1和1″;侧平大圆上的点Ⅱ,由2′而确定2″和2;水平大圆上的点Ⅳ,由4′直接确定4和4″;最右点也是最高点Ⅴ就是侧平圆弧的端点;最前点Ⅲ的作法和图3-19类似,也可以过球心作积聚线的垂线,垂足就是3′,再过3′作水平纬圆,从而得到3和3″。
②纬圆法作一般点A(a′-a-a″)。
③对称作出后一半的点,并依次连接各点成光滑的曲线,最后判别可见性和处理轮廓线。
说明:虽然这里的正垂圆弧落在了球的左下方和右方,但是由于球的左上方被切掉而不存在了,所以其H、W投影均是可见的。
3.6 回转体的相贯线
3.6.1 平面立体与回转体的相贯线
平面立体与回转体的相贯线,一般是由一些平面曲线或者平面曲线和直线组成的闭合的空间曲线。实际上就是由平面立体的各表面与回转体表面的截交线的组合。同样有“全贯”和“互贯”之分。
随着平面立体和回转体对投影面的相对位置不同,分两种情况讨论。
1)回转体的投影具有积聚性
根据相贯线是共有线的特点,当回转体的投影具有积聚时,求相贯线的问题就转化为在平面立体表面取点、线来解决。
【例3-14】 求作图3-21(a)所示两立体的相贯线。
【解】 这是一个四棱锥和圆柱相贯,它们的轴线都垂直于H面,圆柱的H投影积聚为圆。根据相贯线是共有线的性质,组成该圆的四段弧也分别在四棱锥的4个表面上,知道其H投影,用平面上取点、线的方法求作其V、W投影。图形是左右、前后对称的,仅介绍前侧面的作图,如图3-21(b)所示。

图3-21 回转体具有积聚性的平-曲相贯
①作控制点:由H投影可知,最左点Ⅰ(1)、最右点Ⅲ(3)分别在左右棱线上,离锥顶最近,所以也是最高点;最前点Ⅱ(2)离锥顶最远,所以也是最低点。它们可以直接作出。
②用辅助线法增加一般点A、B(a、b-a′、b′-a″、b″)。
③依次连接各点成光滑的曲线,并处理轮廓线。
2)平面体的投影具有积聚性
当平面体的投影具有积聚时,求相贯线的问题就转化为在曲面立体表面取点、线来解决。
【例3-15】 求作图3-22(a)所示两立体的相贯线。
【解】 这是一个三棱柱和圆锥互贯的问题。三棱柱的V投影具有积聚性,所以根据相贯线是共有线的性质,问题可转化为在圆锥面上取点、线来解决。这里的相贯线实际上就是三棱柱的右侧面LM和下底面MN分别和圆锥的截交线:下底面MN截得的截交线为水平圆弧,其H投影反映实形,V、W投影积聚为水平直线;右侧面LM截得的截交线为椭圆弧,V投影积聚为直线,H、W投影仍然是椭圆弧。
作图过程如图3-22(b)所示。其中椭圆弧的画法可参照图3-19。读者自己可以对各个点进行编号。

图3-22 平面体具有积聚性的平-曲相贯
3.6.2 两回转体的相贯线
两个回转体的相贯线,一般情况下是闭合且光滑的空间曲线,特殊情况下为平面曲线或直线。下面分别讨论这两种情况下的相贯线的投影特点及求法。
1)一般情况
这里所说的一般情况是指两个回转体的直径大小及轴线之间的相对位置不符合特定的情况。当然,工程上常见的两个回转体相贯中一般至少有一个是圆柱,而且圆柱的投影具有积聚性,因此求两个回转体的相贯线问题就可以转化为在另一个回转体表面取点、线来解决。
【例3-16】 求作图3-23(a)所示两立体的相贯线。
【解】 这是两个轴线分别垂直于H、W的铅垂圆柱和侧垂圆柱相贯的问题。铅垂圆柱的H投影积聚为圆,侧垂圆柱的W投影积聚为圆,所以只需要求作相贯线的V投影。因为侧垂圆柱完全穿过铅垂圆柱,因此属于全贯,相贯线分左、右两支。
作图过程如图3-23(b)所示。
这里的特殊点和一般点,也请读者自己分析标注。

图3-23 两个圆柱的相贯线
注意,对于轴线正交的两个圆柱相贯,其相贯线还可以用圆弧代替,其画法如下:
①在V投影上,先以两个圆柱的轮廓线的交点1′为圆心,大圆柱的半径R为半径作圆弧,交小圆柱的轴线于O′点。
②再以O′点为圆心,大圆柱的半径R为半径作圆弧,即得所求相贯线。
【例3-17】 求作图3-24(a)所示两立体的相贯线。
【解】 这是一个侧垂圆柱和铅垂圆锥全贯的问题。侧垂圆柱全部横穿铅垂圆锥,所以相贯线分左右对称的两支。因为两个立体的轴线是相交的,所以每支相贯线的前后也是对称的。由于侧垂圆柱的W投影具有积聚性,因此,根据相贯线是共有线的性质,此问题就转化为在圆锥表面取点、线来解决V、H投影。作图过程如图3-24(b)所示。


图3-24 圆柱和圆锥的相贯线
①作特殊点:圆柱的最高、最低轮廓线与圆锥的最左轮廓线分别交于最高点Ⅰ和最低点Ⅴ(同时也是最左点),可以直接作出其投影;最前点Ⅲ用纬圆法作出;左、右两支相贯线的最右、最左点位于过锥顶作圆柱切线的切点处,在W投影中过锥顶作圆的切线s′a′、s′b′,切点为m″、n″,用素线法作出其对应的m′、n′和m、n。
②用纬圆法作出一般点Ⅱ和Ⅳ。
③按对称性作出后一半和右侧相贯线上的各点,连接各点成光滑的曲线并判别可见性和处理轮廓线。
2)特殊情况
这里所说的特殊情况,是指两个回转体的大小或者轴线处于特殊情况,其时的相贯线又有直线、圆和椭圆等几种。
(1)相贯线为直线的情况
当两个圆柱轴线平行(如图3-25(a))或者两个圆锥共锥顶(如图3-25(b))时,其相贯线为直线。

图3-25 相贯线为直线的情况
(2)相贯线为圆的情况
如图3-26所示,当两个回转体共轴线时,其相贯线为圆。

图3-26 相贯线为圆的情况
(3)相贯线为平面曲线——椭圆的情况
如图3-27所示,当两个回转体共切于一个球时,其相贯线为椭圆。
当两个回转体的轴线正交时,其相贯线为两个大小相等的椭圆,如图3-27(a)、(c);当两个回转体的轴线斜交时,其相贯线为两个大小不等的椭圆,如图3-27(b)、(d)。由于是同一个圆柱相贯的,所以两个椭圆的短轴还是相等的。
在如图3-27所示的4个图中,由于两个回转体的轴线都是平行于V面的,所以相贯线的V投影都积聚为直线。对于H投影,图3-27(a)、(b)具有积聚性,而图3-27(c)、(d)没有积聚性,其投影一般仍是椭圆。

图3-27 相贯线为椭圆的情况
3.7 工程中常见的直纹曲面
除了上述回转曲面体以外,一些规则或不规则的曲面由于其流畅、平滑和造型美观,如今在建筑工程中得到了越来越广泛的应用,如国家体育馆——鸟巢,是2008年第29届奥林匹克运动会的主体育场,其主体结构和屋面大量采用了不规则曲线和曲面元素。但是应用得比较成熟,同时施工也比较方便的还是一些有规则的直纹曲面。
3.7.1 单叶双曲回转面
一直母线绕着与之交叉的轴线旋转而形成的曲面称为单叶双曲回转面。如图3-28所示,直母线AB绕着与之交叉的轴线O1O2旋转,得到的曲面就是单叶双曲回转面。单叶双曲回转面经常用于水塔、电视塔和冷凝塔等工程中,图3-29所示的冷凝塔就是单叶双曲回转面的具体应用。

3-28 单叶双曲回转面的形成

图3-29 单叶双曲回转面的应用
【例3-18】 如图3-30(a)所示,已知直母线MN绕轴线O1O2旋转,求作该单叶双曲回转面的投影。
【解】 作图步骤如下:
①直母线旋转时,两个端点的运动轨迹是垂直于轴线而平行于H面的纬圆。以轴线的H面投影为圆心,分别以O1m和O2n为半径作同心圆,如图3-30(b)所示。
②在H面投影上,把两个纬圆分别从m、n开始,均分成相同的等份(图中为12等份),mn顺时针旋转30°(即圆周的十二分之一)后,就得到素线PQ的H面投影pq,由pq向上引投影连线,得到V面投影p′q′,如图3-30(c)所示。
③顺次作出每旋转30°后各素线的H面投影和V面投影。在V面上,引平滑曲线作为包络线与各素线的V面投影相切,即为双曲线。在H面上,作各素线的包络线,即为该曲线的颈圆。如图3-30(d)所示。

图3-30 单叶双曲回转面的画法
3.7.2 柱状面
一直母线沿着两条曲导线且始终平行于一导平面运动所形成的曲面 ,称为柱状面 。如图3-31(a)所示,直母线AC,沿着曲线AB和曲线CD移动,并始终平行于导平面P。当导平面平行于W面时,该柱状面的投影如图3-31(b)所示。

图3-31 柱状面的投影
柱状面常用于壳体屋顶、隧道拱及钢管接头等。
3.7.3 锥状面
一直母线沿着一直导线和一曲导线且始终平行于一导平面运动所形成的曲面 ,称为锥状面 。如图3-32(a)所示,直母线AC沿着直导线CD和曲导线AB移动,且始终平行于导平面P。当导平面平行于W面时,该锥状面的投影如图3-32(b)所示。
锥状面常用于壳体屋顶及雨篷等。

图3-32 锥状面的投影
3.7.4 双曲抛物面
一直母线沿着两交叉直导线且始终平行于一导平面运动所形成的曲面 ,称为双曲抛物面 。如图3-33所示,直母线AC沿着交叉直线AB和CD移动,且始终平行于导平面P,此曲面也称马鞍面 。双曲抛物面被应用于许多大型建筑的屋面。
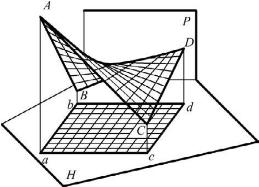
图3-33 双曲抛物面的形成
【例3-19】 如图3-34(a)所示,已知直母线沿着导线AB和CD运动且始终平行于导平面P,试作出该双曲抛物面的投影图。
【解】 作图步骤如下:
①将直导线分成若干等份(图中为6等份),分别连接各等分点的对应投影,如图3-34(b)所示。
②在V面上,用平滑曲线作为包络线与各素线的V面投影相切,即为一条抛物线,如图3-34(c)所示。
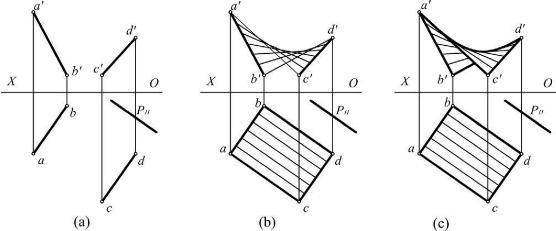
图3-34 双曲抛物面的画法
3.7.5 平螺旋面
一直母线沿着圆柱螺旋线和圆柱轴线 ,且始终平行于与圆柱轴线垂直的导平面移动而形成的曲面 ,称为平螺旋面 ,如图3-35所示。
平螺旋面投影图的作图步骤如图3-35(a)所示:
(1)画出圆柱螺旋线和圆柱轴线的H面投影和V面投影。
(2)将圆柱螺旋线H面投影沿着圆周分成若干等份(图中为12等份),并将等分点与圆心相连,连线即为平圆柱螺旋面上素线的H面投影。
(3)将圆柱螺旋线V面投影也分成相同等份,过各等分点作水平线与轴线相交,这些水平线即为平圆柱螺旋面上素线的V面投影。
图3-35(b)所示的是平螺旋面被一个同轴小圆柱所截的情况,它在建筑工程中随处可见,比如用作图3-36所示的旋转楼梯等。

图3-35 平螺旋面

图3-36 平螺旋面的应用
【例3-20】 已知螺旋楼梯所在的内外螺旋面的投影图,如图3-37(a)所示。试作出螺旋楼梯的投影。
【解】 在螺旋楼梯的每一个踏步中,踏面为扇形,踢面为矩形,两端面为圆柱面,底面为螺旋面。设第一个踏步踏面4个角点分别为Ⅱ1、Ⅱ2、Ⅲ2、Ⅲ1,踢面4个角点分别为Ⅰ1、Ⅰ2、Ⅱ2、Ⅱ1。第二个踏步踏面4个角点分别为Ⅳ1、Ⅳ2、Ⅴ2、Ⅴ1,踢面4个角点分别为Ⅲ1、Ⅲ2、Ⅳ2、Ⅳ1。具体画法如下:
①将内外导圆柱在H面的投影分为12等份,得到12个扇形踏面的水平投影。在水平投影上作出第一个、第二个踏步踏面和踢面各角点的水平投影,如图3-37(a)所示。
②画第一个踏步的V面投影。第一个踢面Ⅰ1Ⅰ2Ⅱ2Ⅱ1的H面投影积聚成一个水平线段(11)(12)2221。分别过点1′1、点1′2向上引垂线,截取一个踏步的高度,得到点2′1、点2′2,矩形1′11′22′12′2为第一个踏步踢面的V面投影,2′12′23′13′2为第一个踏步踏面的V面投影,如图3-37(b)所示。
③画第二个踏步的V面投影。第二个踢面Ⅲ1、Ⅲ2、Ⅳ2、Ⅳ1的H面投影积聚成一斜线段(31)(32)4241。分别过点3′1、点3′2向上引垂线,截取一个踏步的高度,得到点4′1、点4′2,矩形3′13′24′14′2为第二个踏步踢面的V面投影,4′14′25′15′2为第二个踏步踏面的V面投影,如图3-37(c)所示。
以此类推,依次画出其余各踏步踢面和踏面的V面投影。当画到第四至第九级踏步时,由于本身遮挡,踏步的V面投影大部分不可见,而可见的是底面的螺旋面。
④最后画楼梯底面的投影。可对应于梯级螺旋面上的各点,向下截取相同的高度,求出底板螺旋面相应各点的V面投影。比如,第七个踏步踢面底线的两个端点是M1、M2。从它们的V面投影m′1、m′2向下截取梯板沿竖直方向的厚度,得到点n′1、n′2,即所求梯板底面上与M1、M2相对应的两点N1、N2的V面投影。同法求出其他各点后,用光滑曲线连接,即为梯板底面的V面投影。完成后的螺旋楼梯两面投影,如图3-37(d)所示。

图3-37 螺旋楼梯的画法
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















