垂直投影示意图

5　轴测投影

多面正投影图具有度量性好、作图简便等特点，能够准确而完整地表达物体各个方向的形状与大小，因此在工程制图中被广泛采用。然而，多面正投影图缺乏立体感，直观性较差，读者必须具备一定的读图能力才能看懂。如图5－1（a）所示的三面投影图缺乏立体感，不容易直接看出所示形体的空间形状，而图5－1（b）所示的该形体的轴测投影图能够在一个平面上同时反映出形体的长、宽、高3个方向的尺度，立体感较强，具有非常好的直观性。因此，工程上也常用这种图样帮助正投影图形象、直观地表达工程建筑物的立体形状。

图5－1　多面正投影图与轴测投影图

5.1　轴测投影的基本知识

5.1.1　轴测投影图的形成和作用

将空间形体及确定其位置的直角坐标系按照不平行于任一坐标面的方向S一起平行地投射到一个平面P上，所得到的图形叫做轴测投影图 ，简称轴测图 ，如图5－2所示。其中，方向S·称为投射方向 ，平面P·称为轴测投影面 。由于轴测图是在一个面上反映物体3个方向的形状，不可能都反映实形，其度量性较差，且作图较为繁琐，因而在工程中一般仅作为多面正投影图的辅助图样。

5.1.2　轴间角和轴向变形系数

如图5－2所示，空间直角坐标系投影为轴测坐标系，OX、OY、OZ轴的轴测投影分别为O1X1、O1Y1、O1Z1，称为轴测投影轴 ，简称轴测轴 ；轴测轴之间的夹角，即∠X1O1Z1、∠X1O1Y1、∠Y1O1Z1称为轴间角 ；轴测轴上的线段长度与相应直角坐标轴上的线段长度的比值称为轴向变形系数 ，分别用p、q、r表示，则：

p＝，p称为X轴向变形系数；

q＝，q称为Y轴向变形系数；

r＝，r称为Z轴向变形系数。

图5－2　轴测投影图的形成

5.1.3　轴测投影图的分类

根据投射方向是否垂直于轴测投影面，轴测投影可分为两大类：当投射方向与轴测投影面垂直时，称为正轴测投影 ；当投射方向与轴测投影面倾斜时，称为斜轴测投影 。如图5－3（a）所示，空间形体在投影面P上的投影为正轴测投影，其投射方向S1与投影面P垂直；空间形体在投影面Q上的投影为斜轴测投影，其投射方向S2与投影面Q倾斜。而且随着空间形体及其坐标轴对轴测投影面的相对位置的不同，轴间角与轴向变形系数也随之变化，从而得到各种不同的轴测图。正轴测投影和斜轴测投影各有3种类型：

正等测：p＝q＝r；

正二测：p＝r≠q或p＝q≠r、q＝r≠p；

正三测：p≠q≠r；

斜等测：p＝q＝r；

斜二测：p＝r≠q或p＝q≠r、q＝r≠p；

斜三测：p≠q≠r。

工程上常用正等测和正面斜二测（p＝r≠q）。

图5－3　轴测投影图的分类

5.1.4　轴测投影的特性

由于轴测投影属于平行投影，因此具备平行投影的一些主要性质：

（1）空间互相平行的线段 ，它们的轴测投影仍互相平行 。因此 ，凡是与坐标轴平行的线段 ，其轴测投影与相应的轴测轴平行 。

（2）空间互相平行线段的长度之比 ，等于它们轴测投影的长度之比 。因此 ，凡是与坐标轴平行的线段 ，它们的轴向变形系数相等 。

所谓 “轴测 ”，就是轴向测量之意。所以作轴测图只能沿着与坐标轴平行的方向量取尺寸，与坐标轴不平行的直线，其变形系数不同，不能在轴测投影中直接作出，只能按坐标作出其两端点后才能确定该直线。

5.2　正等测投影图

5.2.1　轴间角和轴向变形系数

当投射方向与轴测投影面相垂直，且空间形体的3个坐标轴与轴测投影面的夹角相等时所得到的投影图，称为正等测投影图 ，简称为正等测 。如图5－4所示，空间直角坐标系OXYZ沿着OO1的方向垂直投影到P平面上，由于3个坐标轴与P平面所成的角度相等，所以3个交点A、B、C构成一个等边三角形，3条中线O1A、O1B、O1C（也是3个坐标轴的方向）之间的夹角相等。即：3个轴间角∠X1O1Z1＝∠X1O1Y1＝∠Y1O1Z1＝120°。正等测的轴向变形系数理论值为p＝q＝r＝0.82，但为作图简便，常取简化值1，而且一般将O1Z1轴作为铅直方向，如图5－5所示。

图5－4　正等测图的形成

图5－5　正等测图的轴间角

5.2.2　正等测图的画法

在绘制空间形体的轴测投影图之前，首先要认真观察形体的结构特点，然后根据其结构特点选择合适的绘制方法。主要有坐标法、叠加法和切割法等。

1）坐标法

根据物体上各顶点的坐标，确定其轴测投影，并依次连接，这种方法称为坐标法 。

【例5－1】　已知三棱台的两面投影图如图5－6（a）所示，绘制其正等轴测投影图。

【解】　作图步骤如下：

①建立坐标系，作轴测轴并确定轴间角和轴向变形系数（正等测轴间角均为120°，轴向变形系数取1），如图5－6（a）所示。这里需注意，为使作图简便，应使坐标轴尽可能地通过形体上的点或线，如OX轴通过A点，OY轴通过C点。

②在对应轴测轴上截取O1A1＝oa，O1C1＝oc，量取B点的X、Y坐标，从而确定B1点，如图5－6（b）所示。

③为方便确定三棱台的上底，可以先作出三棱台的虚拟锥顶S1，从而确定各个棱线的方向，以方便在各棱线上确定上底面的各个端点，如图5－6（c）所示。

④将可见的各棱边和棱线加深，即完成该三棱台的正等轴测图，如图5－6（d）所示。

在轴测图中一般不画不可见的轮廓线，最后的轴测轴也不需要画。因此，在确定坐标系时要注意坐标原点的选择：对于对称形体，坐标原点宜确定在图形的中心处，如图5－7所示；对于柱体，坐标原点可确定在形体的左前下角（或右前下角），从而避免画右后方（或左后方）不可见的轮廓线，如图5－8所示。

图5－6　坐标法绘制正等测图

图5－7　以图形的中点作为坐标原点

2）叠加法

对于由多个基本体叠加而成的空间形体，宜在形体分析的基础上，在明确各基本体相对位置的前提下，将各个基本体逐个画出，并进行综合，从而完成空间形体的轴测投影图，这种画法称为叠加法。画图顺序一般是由下而上、先大后小。

【例5－2】　如图5－8（a）所示，已知某空间形体的两面投影，绘制其正等轴测投影图。

【解】　该空间形体由一个水平放置的四棱柱、一个直立的四棱柱与一个三棱柱三部分叠加而成，其作图步骤如下：

①根据坐标法和轴测投影特性绘制水平四棱柱（注意坐标原点的选择），如图5－8（b）所示。

②根据两个四棱柱的相对位置关系，在水平四棱柱上绘制直立四棱柱，如图5－8（c）所示。

③根据三棱柱的底面形状及其与两个四棱柱的位置关系，绘制三棱柱，并处理和加深轮廓线，完成轴测投影图，如图5－8（d）所示。

图5－8　叠加法绘制正等测图

3）切割法

对于有些形体，宜先画出假想完整的基本体，然后在此基础上再进行切割，这种方法称为切割法 。

【例5－3】　如图5－9（a）所示，已知某空间形体的两面正投影图，绘制其正等测图。

【解】　该形体可看成一个大的四棱柱在左上侧切去另外一个小的四棱柱，然后在左前侧再切去一个三棱柱而成。作图步骤如下：

①绘制大四棱柱的轴测投影图，如图5－9（b）所示。

②在大四棱柱的左上侧切去一个小四棱柱，如图5－9（c）所示；并继续切去左前侧的三棱柱，从而完成空间形体的轴测投影图，如图5－9（d）所示。

图5－9　切割法绘制正等测图

5.2.3　平行于坐标面的圆的正等轴测投影

圆的正等测投影为椭圆。由于3个坐标面与轴测投影面所成的角度相等，所以直径相等的圆，在3个轴测坐标面上的轴测椭圆大小也相等，且每个轴测坐标面（如X1O1Y1及与之平行的面）上的椭圆的长轴垂直于第三轴测轴（O1Z1）。如图5－10所示。

图5－10　平行于坐标面的圆的正等测图

1）圆的正等测画法

圆的正等测图可以采用四心圆法近似画出，它是用4段圆弧近似的代替椭圆弧，可大大提高画图速度。作图过程如图5－11所示。

（1）画出圆外切正方形的轴测投影——菱形，并确定4个圆心，如图5－11（b）所示：其中短对角线的两个端点O1、O2为两个圆心；O1A1、O1D1与长对角线的交点O3、O4为另外两个圆心。

（2）分别以O1、O2为圆心，O1A1为半径画弧和，以O3、O4为圆心，O3A1为半径画弧和，即完成全图，如图5－11（c）所示。

图5－11　四心法绘制圆的正等测图

2）圆角的正等测画法

一般的圆角，正好是圆周的四分之一，因此它们的轴测图正好是近似椭圆4段弧中的一段。可采用圆的正等轴测投影的画法：过各圆角与连接直线的切点，作对应直线的垂线，两对应垂线的交点即为相应圆弧的圆心，半径则为圆心至切点的距离，如图5－12所示。

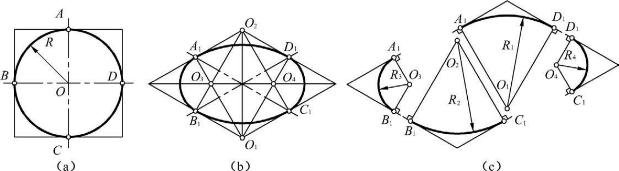
图5－12　正等测图中圆角的画法

实际作图时，需要注意圆或圆弧是在哪个坐标方向的，方向不同，边及相应的垂线方向也随之变化（效果见图5－15，读者可尝试在图上作出各个方向圆弧的切线及对应的圆心，以体会圆和圆弧的正等测画法）。

5.3　斜轴测投影

5.3.1　轴间角和轴向变形系数

在绘制斜轴测投影时，为了作图方便，通常使形体的某个特征面平行于轴测投影面，其轴测投影反映实形，相应的有两个轴测轴的变形系数为1，对应的轴间角仍为直角；而另一个轴测轴可以是任意方向（通常取与水平方向成30°、45°或60°等的特殊角），对应的变形系数也可以取任意值，通常取0.5，既美观又方便。

例如，当坐标面XOZ与轴测投影面P平行时，轴间角∠X1O1Z1＝90°，相应的p＝r＝1，q＝0.5，O1Y1方向可任意选定，由此得到的轴测投影称为正面斜轴测投影 ；同样还有水平斜轴测投影和侧面斜轴测投影，相应的特点请读者自己分析。

5.3.2　常用的两种斜轴测投影图

工程上常用的两种斜轴测投影图分别是正面斜二测图和水平斜等测图。

1）正面斜二测图

正面斜二测就是物体的正面平行于轴测投影面，轴间角∠X1O1Z1＝90°，轴向变形系数p＝r＝1，q＝0.5（也可以取任意值）。其轴测轴O1X1画成水平，O1Z1画成竖直，轴测轴O1Y1则与水平方向成45°角（也可画成30°角或60°角）。如图5－13所示。

图5－13　正面斜二测图

当轴向变形系数p＝q＝r＝1时，则为正面斜等测图。

2）水平斜等测图

水平斜等测图一般用于表达某个小区或建筑群的鸟瞰效果。通常将轴测轴O1Z1画成竖直，O1X1与水平成60°、45°或30°角。轴间角∠X1O1Y1＝90°，∠X1O1Z1＝120°、135°或150°，轴向变形系数p＝q＝r＝1。也就是将平面图旋转30°（或者45°和60°）后，向上竖各部分的高度。如图5－14（a）、（b）所示为某建筑群的平面图及其水平斜等测图。

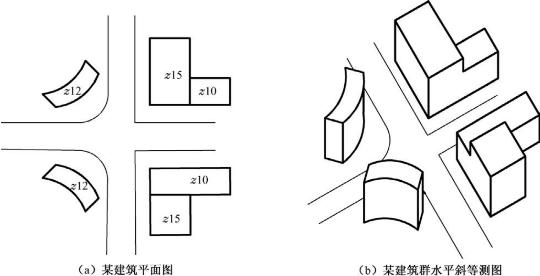
图5－14　水平斜等测图

5.4　轴测投影的选择

在绘制轴测图时，首先需要解决的是选用哪种类型的轴测图来表达空间形体，轴测类型的选择直接影响到轴测图表达的效果。在轴测图类型确定之后，还需考虑投影方向，从而能够更为清晰、更为明显地表达重点部位。总之，应以立体感强和作图简便为原则。

5.4.1　轴测投影类型的选择

由于正等测图的3个轴间角和轴向变形系数均相等，尤其是平行于3个坐标面的圆的轴测投影画法相同，且作图简便。因此，对于锥体及其切割体和多个坐标面上有圆 、半圆或圆角的形体 ，宜采用正等测 。如图5－15所示。

图5－15　轴测图种类的选择

斜二测适用于特征面和某一坐标面平行且形状比较复杂的柱体，因为此时该特征面在斜二测图中能够反映实形，画图较为方便，如图5－13所示。

5.4.2　投影方向的选择

在确定了轴测投影图的类型之后，根据形体自身的特征，还需要进一步确定适当的投影方向，使轴测图能够清楚地反映物体所需表达的部分。具体来说，有如下原则：

（1）当形体的左前上方比较复杂需重点表示时 ，宜选择左俯视 ，如图5－16（a）所示。

（2）当形体的右前上方比较复杂需重点表示时，宜选择右俯视，如图5－16（b）所示。

（3）当形体的左前下方比较复杂需重点表示时，宜选择左仰视，如图5－16（c）所示。

（4）当形体的右前下方比较复杂需重点表示时，宜选择右仰视，如图5－16（d）所示。

为避免画不可见的轮廓线，坐标原点和坐标轴的方向可以按方便作图而确定（即可不按右手法则，只要3个方向的绝对坐标值不变）。

图5－16　轴测图方向的选择