曲面体与曲面体相交

4.4　曲面体与曲面体相交

在一些零件上常常可见到各种立体相交的情形，有时还可见到在曲面体上穿孔，从而形成孔口交线、两孔的孔壁交线等。这些立体表面相交的交线、孔口交线和孔壁交线，均称为相贯线。例如：图4-25（a）所示的油泵，外壳上有两平面立体相交；图4-25（b）所示的汽车上刹车总泵泵体，其外形是由几个不同方向的圆柱体相交而成；图4-25（c）所示的通风管的交叉处，是由两个圆锥与圆柱相交而成。这些都会产生相贯线，在绘图时，要画出这些相贯线，它可以帮助我们分清形体之间的界限，有助于看图。特别是在绘金属板制件展开图时，必须准确地画出相贯线的投影，以便下料。在一般情况下，两曲面立体的相贯线是闭合空间曲线。在特殊情况下，可能是不闭合的，也可能是平面曲线或直线。

图4-25　曲面立体相交

两曲面立体相交，其相贯线是两曲面立体表面的共有线，相贯线上的点是两曲面立体的共有点。求作两曲面立体相贯线的投影，一般是先作出两曲面立体表面的一些共有点的投影，再将这些点光滑地连接起来并判别其可见性，即得相贯线的投影。

求相贯线的投影一般采用三种方法，即表面取点法、辅助平面法和辅助球面法，下面分别讨论这三种方法。

4.4.1　表面取点法

两个曲面体相交，如果其中一个曲面体是轴线垂直于投影面的圆柱，则圆柱在该投影面上的投影积聚为圆，而相贯线的投影也就重合在该圆上。可以利用曲面体表面上的线的一个投影而求另外两个投影的方法，求得相贯线的其他投影。

例4-10　已知两圆柱的三面投影，求作它们的相贯线，如图4-26（a）所示。

分析　由于圆柱的轴线垂直相交，且一个圆柱轴线垂直于H面，所以水平投影积聚为一圆，相贯线的水平投影就与此圆重合。另一个圆柱轴线垂直于W面，则侧面投影积聚为一圆，相贯线的侧面投影重合在该圆的一段圆弧上。因此，只需求相贯线的正面投影即可。

作图

（1）求特殊点。由相贯线的水平投影，定出最左、最右、最前、最后的四个点A、B、C、D的水平投影a、b、c、d，再在相贯线的侧面投影上相应地作出a″、（b″）、c″、d″，由a、b、c、d和a″、（b″）、c″、d″作出a′、b′、c′、（d′），同时还可看出，A、B点和C、D点分别是相贯线的最高点和最低点。

图4-26　两圆柱相交

（2）求一般点。在相贯线的侧面投影上定出左、右、前、后对称的四个点E、F、G、H的投影e″、（f″）、g″、（h″），再在线贯线的水平投影上作出e、f、g、h，由e″、（f″）、g″、（h″）求得e′、f′、（g′）、（h′）。

（3）将各点光滑地连接，即为所求相贯线的正面投影，如图4-26（b）所示。在正面投影中，前半相贯线在圆柱的可见表面上，所以它们的投影为可见，而后半相贯线的投影为不可见，但与前半部分相贯线的可见投影相重合。

图4-27（a）所示的圆柱穿孔相贯线和图4-27（b）所示的圆筒穿孔时内外相贯线，它们的画法与两圆柱相贯的画法是相同的。

图4-27　两圆柱穿孔相贯的常见情况

例4-11　求作轴线不相交、直径不相等的两圆柱的相贯线投影，如图4-28（a）所示。

分析　两圆柱的轴线垂直不相交，直径小的圆柱轴线垂直于H面，它的水平投影积聚为一圆，相贯线的水平投影与该圆重合。另一直径较大的圆柱轴线垂直于W面，它的侧面投影积聚为一圆，相贯线的侧面投影重合在该圆的一段圆弧上。因此，只需求出相贯线的正面投影即可。

图4-28　轴线不相交的两圆柱相贯线

作图

（1）求特殊点。由相贯线水平投影定出最左、最右、最前、最后的四个点A、B、C、D的投影a、b、c、d，再在相贯线的侧面投影上相应地作出a″、（b″）、c″、d″，有了a、b、c、d和a″、（b″）、c″、d″，就可作出a′、b′、c′、（d′）。G、H两点是相贯线的最高点，其正面投影（g′）、（h′）可由水平投影g、h和侧面投影g″、（h″）求出。

（2）求一般点。在相贯线的水平投影和侧面投影上定出e、f和e″、（f″），按投影规律可求出e′、f′。

（3）判别可见性，并依次光滑连接各个点。从正面投影看，只有同时位于两圆柱的前半圆柱的点才是可见的，a″、b″是可见与不可见的分界点，a′、e′、c′、f′、b′是可见的，连成实线，其余部分位于直立圆柱的后半圆柱面上，因此（g′）、（d′）、（h′）是不可见的，应连成虚线。这样，即可得出相贯线的正面投影，如图4-28（b）所示。

4.4.2　辅助平面法

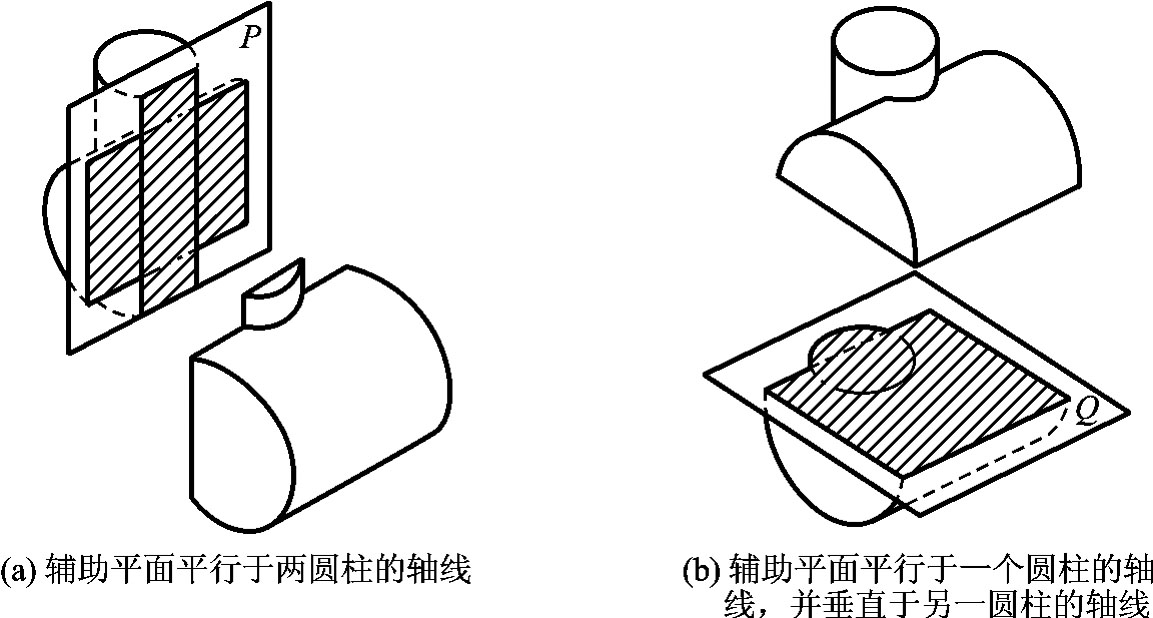
图4-29　用辅助平面法求相贯线上的点

用辅助平面法求相贯线，就是指用辅助平面同时截切相贯的两曲面立体。如图4-29所示，可找出两曲面立体的截交线的交点，即相贯线上的点，这些点既是曲面体表面上的点，又是辅助平面上的点。因此，辅助平面法就是利用三点共面法原理，用若干个辅助平面求出相贯线上一系列的点。

利用辅助平面法求相贯线时，选择辅助平面的原则是使用与两曲面体的截交线的投影为最简单的辅助平面，如直线和圆。

例4-12　求作轴线互相垂直的圆锥与圆柱的相贯线，如图4-30所示。

分析　由图4-30可以看出，圆锥和圆锥轴线垂直相交，具有前后对称平面。因此，相贯线是一前后对称的闭合空间曲线，它的前后两部分的正面投影重合。相贯线的侧面投影重合在圆柱具有积聚性的投影圆上，所要求的是相贯线的水平投影和正面投影。

作图

（1）求特殊点。在侧面投影的圆上，可直接得到最高点和最低点A、C的投影a″、c″，在正面投影中两曲面体的轮廓线交点即a′、c′，由a″、c″和a′、c′可以求得水平投影a、c。在侧面投影中，可直接得到最前点和最后点B、D的投影b″、d″。过B、D作一水平辅助平面QV，它与圆锥的交线为一水平圆，与圆柱的交线为两条平行直线，两交线的交点即为相贯线上的点，如图4-30所示，由此可得b、d、b′、（d′）。b、d也是相贯线水平投影可见与不可见的分界点。

图4-30　圆柱与圆锥的相贯线

（2）求一般点。如图4-30所示，作水平辅助平面Q1V和Q2V，利用其具有积聚性的侧面投影分别作出它们与两个曲面交线的水平投影，其交点为e、f和（g）、（h），即相贯线上E、F、G、H的水平投影，由e、f、（g）、h可得e′、（f′）、g′、（h′）。

（3）判别可见性，并依次光滑连接各点。由于相贯线前后对称，所以正面投影前后重合，画成实线，圆柱的上半部分与圆锥面水平投影均为可见，因此相贯线的水平投影以b、d为分界点，b、e、a、f、d用实线相连，（g）、（c）、（h）不可见，用虚线相连。

例4-13　求作圆台与半圆球的相贯线，如图4-31（a）所示。

分析　由图4-31（a）可见，圆台的轴线不通过半圆球的圆心，圆台和半球有公共的前后对称面。因此，相贯线是前后对称的闭合空间曲线。前半部分相贯线和后半部分相贯线的正面投影重合，相贯线的水平投影都是对称的曲线。由于两曲面体表面的三个投影都没有积聚性，因此，相贯线的三个投影都必须画出。

图4-31　圆台与半圆球的相贯线

作图

（1）求特殊点。在正面投影中，圆台与半圆球两曲面体轮廓线的交点a′、b′即为相贯线的最低点和最高点，A、B的正面投影也是相贯线正面投影可见与不可见的分界点。由a′、b′作出a、b和a″、b″。

作通过圆台轴线的侧平面P，与圆台表面相交于最前、最后素线，与半圆球表面的截交线为一圆。作出它们侧面投影的交点c″、d″，即为相贯线在圆台最前、最后素线上的点C、D的侧面投影，也就是相贯线侧面投影的可见与不可见的分界点。圆台的侧面投影轮廓线应画到c″、d″为止。由c″、d″可作出c′、（d′）和c、d。

（2）求一般点。在a和b之间作水平面QV，与圆台表面和圆球表面的截交线都为水平圆，作出它们的水平投影，两圆交点e、f即为相贯线上的两个一般点E、F的水平投影，再由e、f和e′、（f′）作出e″、f″。同理，再作辅助平面，可求出其他点。

（3）分别依次光滑连接所作出的各点的同面投影，即得相贯线的同面投影。相贯线正面投影的前半部分和后半部分重合，前半部分可见画成实线；水平投影均可见，画成实线；同样，侧面投影c″、e″、a″、f″、d″可见，画成实线，而（b″）不可见，与之相连的线画成虚线。圆球的外形轮廓线被遮住的部分也应画成虚线。

4.4.3　辅助球面法

当两曲面体的轴线相交，且平行于某个投影面时，我们可用辅助球面法求其相贯线。

辅助球面法的基本原理是：曲面体与球相交，当球心在曲面体的轴线上时，球与曲面体表面的相贯线为一垂直于曲面体轴线的圆。图4-32所示为曲面体与球相交的例子，曲面体轴线都是铅垂线，球心都在轴线上，相贯线都是垂直于轴线的圆，其正面投影都是一直线，水平投影反映圆的实形。

图4-32　曲面体与球相交

例4-14　求圆柱与圆锥斜交的相贯线，如图4-33（a）所示。

分析　两曲面体的轴线相交，且都平行于V面，可利用辅助球面法求相贯线。球面与圆柱和圆锥的截交线都是圆，这些圆的正面投影为直线，因为这些圆都是属于同一球面，所以它们的交点就是相贯线上的点。

图4-33　用辅助球面法求相贯线

作图

（1）先确定相贯线的最高点和最低点，即两曲面体轮廓线在正面投影上的交点a′、b′，并确定辅助球面的最大半径R1和最小半径R2。R₁是相贯线上距圆心最远点a′到球心o′的距离，R₂是内切于圆锥的球面。以o′为圆心、R₂为半径作球面，分别与两曲面体相交，交线圆的正面投影积聚为直线，两直线的交点c′、（d′）即为相贯线上的点。

（2）在最大与最小球面的范围内，以R₃为半径作辅助圆得交点e′、（f′），还可作若干个辅助球面的一系列交点。

（3）利用在曲面体表面取点的方法，可求出相贯线上点的水平投影，如图4-33（b）所示。

（4）判别可见性，并依次光滑连接各点的同面投影。由于两曲面体前后对称，在正面投影中可见与不可见两部分投影重合，应画成实线。在水平投影中，相贯线有一部分为可见，一部分为不可见，其可见与不可见的分界点在圆柱前后素线上，这两点以上的为可见，画成实线，以下的为不可见，画成虚线，如图4-33（b）所示。

4.4.4　相贯线的特殊情况

两曲面立体相交，其相贯线一般为空间曲线，特殊情况下可为直线。

（1）当曲面体与球体相交且球心在曲面体的轴线上时，相贯线为垂直于轴线的圆，如图4-32所示，该圆的正面投影积聚为一直线，水平投影反映圆的实形。

（2）当两曲面体轴线相交，并公切于一个圆球时，相贯线为两条平面曲线———椭圆，如图4-34所示。

图4-34　相贯线为椭圆

（3）当轴线平行的两圆柱体相交时，相贯线为平行的两条直线，如图4-35所示。

（4）当两圆锥共顶相交时，相贯线为相交直线，如图4-36所示。

图4-35　相贯线为平行直线

图4-36　相贯线为相交直线

画相贯线时，如遇到上述情况，可直接画出相贯线。

4.4.5　影响相贯线形状的各因素及相贯线的近似画法

1.影响相贯线形状的各种因素

相贯线的形状与曲面体的表面形状、两曲面体的相对位置及曲面体的尺寸大小等因素有关，表4-3和表4-4所示为相贯线形状受以上因素影响的变化情况。

表4-3表面性质和相对位置对相贯线的影响

表4-4表面性质和尺寸变化对相贯线的影响

2.相贯线的近似画法

当两圆柱正交且直径相差较大时，其相贯线可以采用圆弧来代替非圆曲线。如图4-37所示，可用大圆柱的半径D/2画出圆弧来代替相贯线。以R＝D/2为半径过两圆柱投影轮廓线的交点画圆弧。

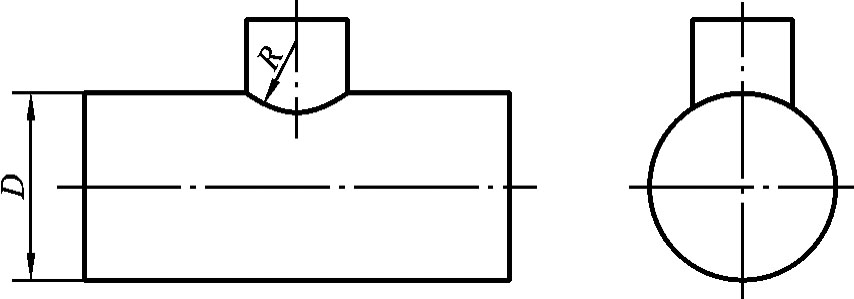
图4-37　用圆弧代替相贯线

4.4.6　组合相贯线

在工程上有时还会遇到三个或三个以上立体相交，其表面将产生几段相贯线，它们的作图方法，可按两立体相贯时的相贯线分别画出。

例4-15　求作如图4-38（a）所示的组合相贯线。

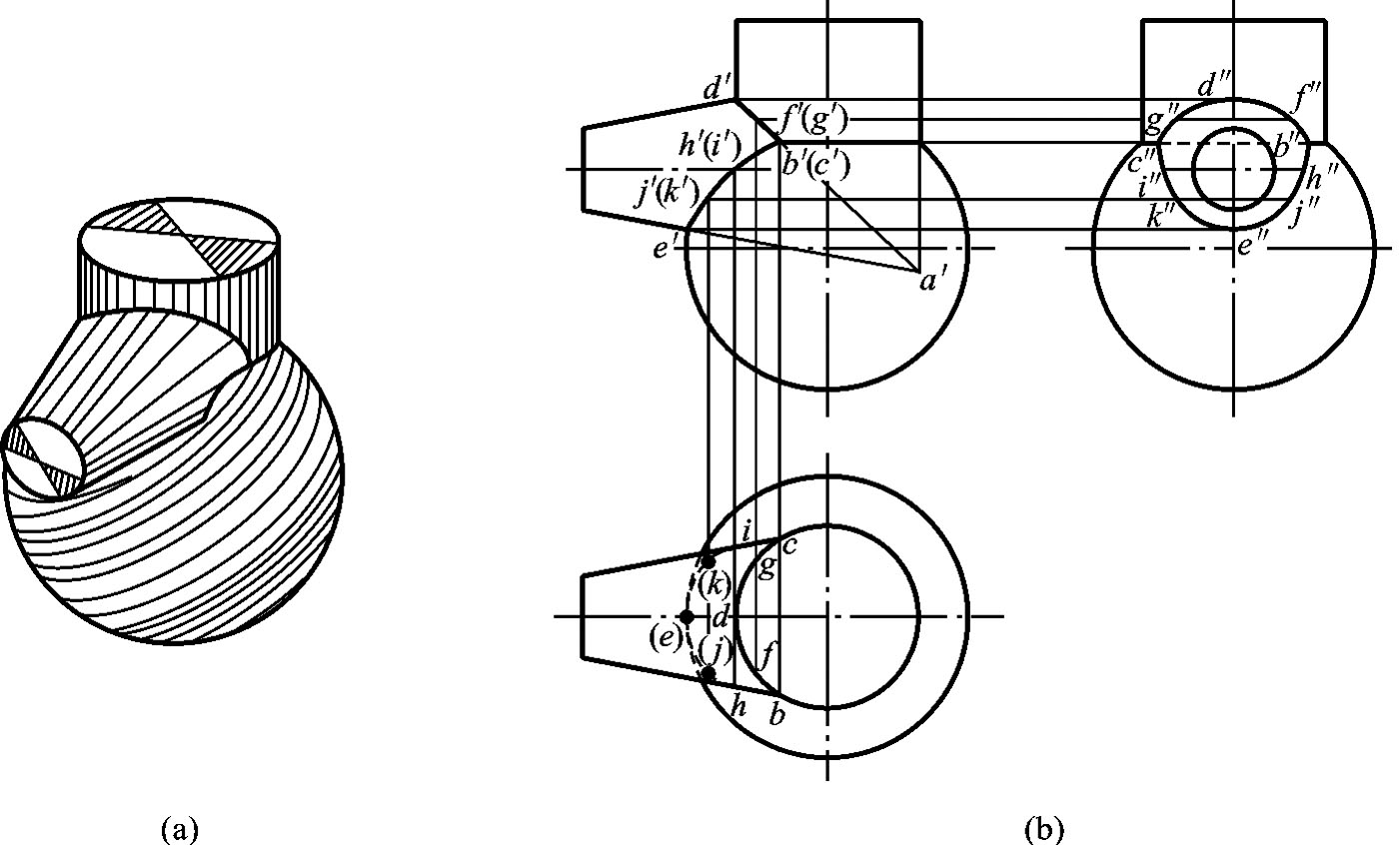
图4-38　组合相贯线

分析　该组合相贯线是由圆柱、圆锥和圆球三个立体相交而形成的。圆柱与圆球的相贯线，由于圆柱的轴线通过圆球球心，相贯线是一圆；圆柱与圆锥的相贯线，因圆锥的水平投影与圆柱的水平投影圆相切，相贯线为一平面曲线，如图4-34（c）所示；圆锥与圆球的相贯线则是一前后对称的空间曲线。找出三段相贯线的结合点，再分别求出两曲面体的相贯线，即得组合相贯线。

作图

（1）求圆柱与圆球的相贯线。因圆柱面的轴线通过球心，故相贯线的正面投影和侧面投影为一直线，水平投影为一圆。

（2）求圆柱与圆锥的相贯线。其正面投影为一直线，作法是延长圆柱及圆锥轮廓线得交点a′，连接d′a′，它与圆柱和球的相贯线交于b′、（c′），b′、（c′）是三段相贯线的分界点，由b′、（c′）可作出b、c和b″、c″，在d′和b′（c′）之间取f′（g′）可作出f、g和f″、（g″）。

（3）圆锥与圆球的相贯线，三面投影均为曲线，可参看例4-13，找出各点的三面投影。

（4）光滑连接各段相贯线上的点的同面投影，即得组合相贯线，如图4-38（b）所示。

可见性的判别：圆柱与球相贯线的侧面投影b″与c″之间为不可见，应画成虚线。正面投影中圆锥轴线以下部分相贯线的水平投影均为不可见，应画成虚线。

在绘制多形体相交的相贯线时，必须进行形体分析和相贯线分析，搞清楚组合体由哪些相贯线组成，哪些表面有相交关系，哪些地方应该有交线存在，以及是什么类型的交线。只有做到心中有数，才能正确地作图。