队列的实现

3.5　队列的实现

与栈类似,队列的实现既可以采用顺序存储结构,也可以采用链式存储结构。下面分别介绍队列的顺序存储结构实现——循环队列,以及链式存储结构实现——链队列。

3.5.1　循环队列

队列的顺序存储结构和顺序栈类似,常借助一维数组来存储队列中的元素,同时设置两个指针front和rear分别指向队首元素和队尾元素的位置。图3－6展示了队列的顺序存储结构。

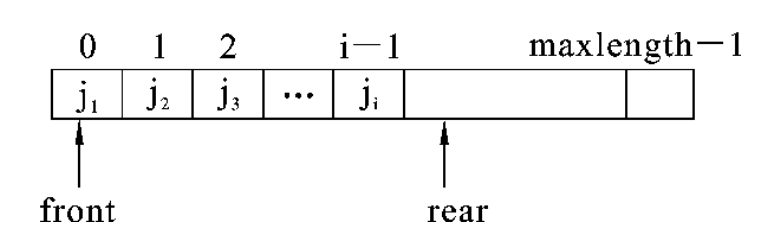
图3－6　队列的顺序存储示意图

由于一维数组定义时需要指定最大长度,因此顺序队列实现时常设置一个符号常量MAXQSIZE来表示队列的最大容量。初始时建立一个空队列（此时front＝rear＝0）,每当插入一个元素时,队尾指针rear增加1；每当删除一个元素时,队首指针front增加1。因此,在一个非空的队列中,队首指针始终指向队首,而队尾始终指向队尾元素的下一个位置。图3－7所示为最大容量为6的顺序队列中,头、尾指针的变化情况。

图3－7　一个队列中元素和头、尾指针的关系

其中,图（a）表示该队列的初始状态为空,此时rear＝front＝0；图（b）表示有3个元素a₁、a₂、a₃相继进入队列,此时rear＝3,front的值不变；图（c）表示a₁、a₂、a₃先后出队,队列又变为空,此时rear＝front＝3；图（d）表示有3个元素a₄、a₅、a₆进入队列,此时front＝3,rear＝6。

倘若还有元素a₇请求进入队列,由于队尾指针已经超出了队列的最后一个位置,因而插入a₇就会发生“溢出”。此时,直接的解决方法是采用顺序栈的解决方法,这样可以扩大存储空间,但这种方法用在此处并不合理,因为这时的队列并非真的满了,事实上,队列中尚有3个空位。也就是说,系统作为队列用的存储空间并没有真正的用完,但队列却发生了溢出,这种现象称作虚溢出。解决虚溢出的方法通常有以下两种。

图3－8　用平移元素的方法克服虚溢出

1）采用平移元素的方法

采用平移元素的方法时,一旦发生虚溢出就把整个队列的元素平移到存储区的首部。如图3－8所示,将a₄、a₅、和a₆平移到0号位置至2号位置,而将a₇插到第3个位置上。显然,平移元素方法的效率是很低的。

2）将整个队列作为循环队列来处理

该方法的思想是将顺序队列想象成一个环形的空间。当发生虚溢出时,将待插入的元素插入到队首位置,如图3－9（a）所示。这样,虽然物理上队尾在队首之前,但逻辑上队首仍然在前,作插入和删除运算时仍按“先进先出”的原则处理。

图3－9　用循环队列的方法克服虚溢出

但是使用该方法需要注意以下问题:根据等式rear＝front＝0,无法判断队空还是队满。图3－9（b）所示为元素a₈和a₉进入队列后的情形。此时队列已满,如果还要插入元素就会发生上溢。而它与图3－9（c）所示队列为空的情形一样,均有front＝rear。由此可见,在循环队列中,根据等式rear＝front无法判断队空还是队满。解决该问题的方法有:设置一个布尔变量来区分队空和队满；或者不设布尔变量,而把尾指针加1后等于头指针作为队满的标志,但此时会损失一个存储空间,也就是说必须用有maxlength＋1个元素的数组才能表示一个长度为maxlength的循环队列。在下面的循环队列的实现中,采用的是第二种方法来解决此问题。

循环队列的定义如下。

下面给出循环队列的几种基本操作的实现方法,包括循环队列置空、求循环队列长度及插入和删除操作等。

1.queinit函数

【算法思想】　构造一个空循环队列,即申请队列所需的全部存储空间,并初始化队首和队尾指针为0。成功初始化队列则返回1,否则返回0。

具体算法如下。

2.quelength函数

【算法思想】　返回循环队列q的元素个数。

具体算法如下。

需要注意的是,求循环队列的长度有两种情况:①q.rear－q.front＞0,该情况如图3－10（a）所示；②q.rear—q.front＜0,该情况如图3－10（b）所示。为了统一表示这两种情况,可以采用求模运算（%）。

3.enque函数

【算法思想】　插入新元素e,使之成为队q队尾元素。成功插入数据返回1,反之返回0。

图3－10　有3个元素的循环队列

具体算法如下。

注意:由于队空和队满均有q.rear＝q.front,为了区分二者,将（q.rear＋1）% MAXQSIZE＝q.front作为队满条件。即当队列还有一个空间时,就认为已经不能插入元素了,如图3－11所示。

图3－11　（rear＋1）%MAXQSIZE＝front队满条件

4.deque函数

【算法思想】　若队列非空,则删除队q的队首元素。用变量e返回其值,并返回成功标志1。

具体算法如下。

3.5.2　链队列

图3－12　链式队列示意图

队列也可以采用链式存储结构实现,队列的链式存储结构简称为链队列。链队列的实质是一个规定只能在表尾进行插入操作,以及在表头进行删除操作的单链表。通常链队列在实现上会设置两个指针,即队首指针front指向删除数据端,队尾指针rear指向插入数据端。链队列具有链式存储结构的优点,例如,可以提高结点插入和删除的效率,可以根据实际需要为每个队列分配相应单元等。图3－12所示的是一个链式队列的一般形式。

队列的结点数据结构描述如下。

为了表示的方便,下面的实现过程中采用带头结点的单链表来表示链队列。带头结点的链队列如图3－13所示。

图3－13　一系列队列操作时指针变化状况

下面给出链队列的基本操作算法实现。

1.queinit函数

【算法思想】　构造一个空链式队列q,为q申请一个头结点,并使队首和队尾指针都指向该结点。成功初始化队列返回1,否则返回0。

具体算法如下。

2.quedestroy函数

【算法思想】　撤销一个队列,为从链式队列的头结点开始,释放所有结点（包括头结点）的空间。成功撤销队列返回1,否则返回0。

具体算法如下。

3.enque函数

【算法思想】　将新元素e插入到队q的尾部,修改队尾指针使之指向新链入的元素。若插入成功则返回1,若存储分配失败则返回0。

具体算法如下。

4.deque函数

【算法思想】　若队q非空,则删除队q的队首元素,用e返回其值,并返回成功标志1,否则返回0。队列设置了头结点,当队列的最后一个元素被删除后,队列的尾指针也消失了,此时应对尾指针重新赋值,令其指向头结点。

具体算法如下。

5.quelength函数

【算法思想】　求队列q中元素的个数,即q的长度。

具体算法如下。