队列的应用举例

3.6　队列的应用举例

队列的应用十分广泛,例如,在操作系统中对资源的请求都用队列来组织,各种应用系统中的事件规划、事件模拟及非线性数据结构中的许多搜索问题也都借助队列来实现。本节以车辆调度为例,介绍队列在实际中的应用。

图3－14所示的是一个车辆调度场。其中,自东向西表示一个单向行驶的主车道,主车道设有进口和出口,其他车道为一些备用车道。现假设有一编号为1,2,…,n的汽车组成的车队以随机的顺序先后进入主车道,要求按车号由小到大的顺序离开主车道。例如,若汽车以（3,6,9,2,4,7,1,8,5）的顺序进入进车道,则表示3号车最先到达,5号车最后到达。现要求将汽车调度为（1,2,3,4,5,6,7,8,9）,即1号车最先离开,9号车最后离开。显然,如果没有备用车道是不能完成这个任务的。于是可假设有k条备用车道,通过备用车道来改变主车道中汽车排列的顺序。

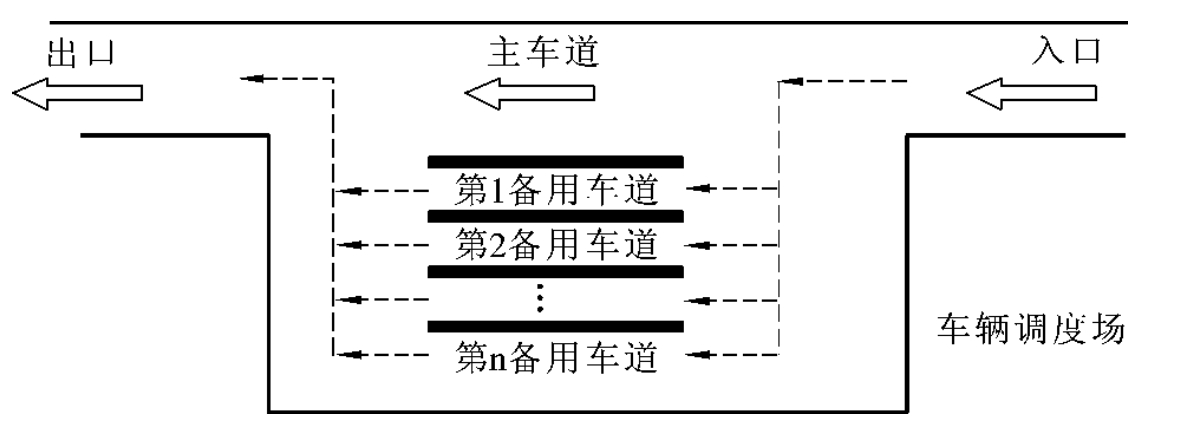
图3－14　车辆调度场示意图

图3－15所示的是用2条备用车道调度上述序列的执行过程,具体的调度方案如下。

首先,3号车进入第一备用车道,接着6号车和9号车相继进入第一备用车道,接下来从图3－15（b）中看到2号、4号和7号车按入口排列的顺序被相继调度到第二备用车道,然后1号车直接到出口,2号车从第二备用道开出并进入出口,3号车从1道开出、4号车从2道开出、8号车进入1道、5号车开往出口、6号车从1道开出、7号车从2道开出、8号车从2道开出、9号车从1道开出,从而完成了车辆的调度。

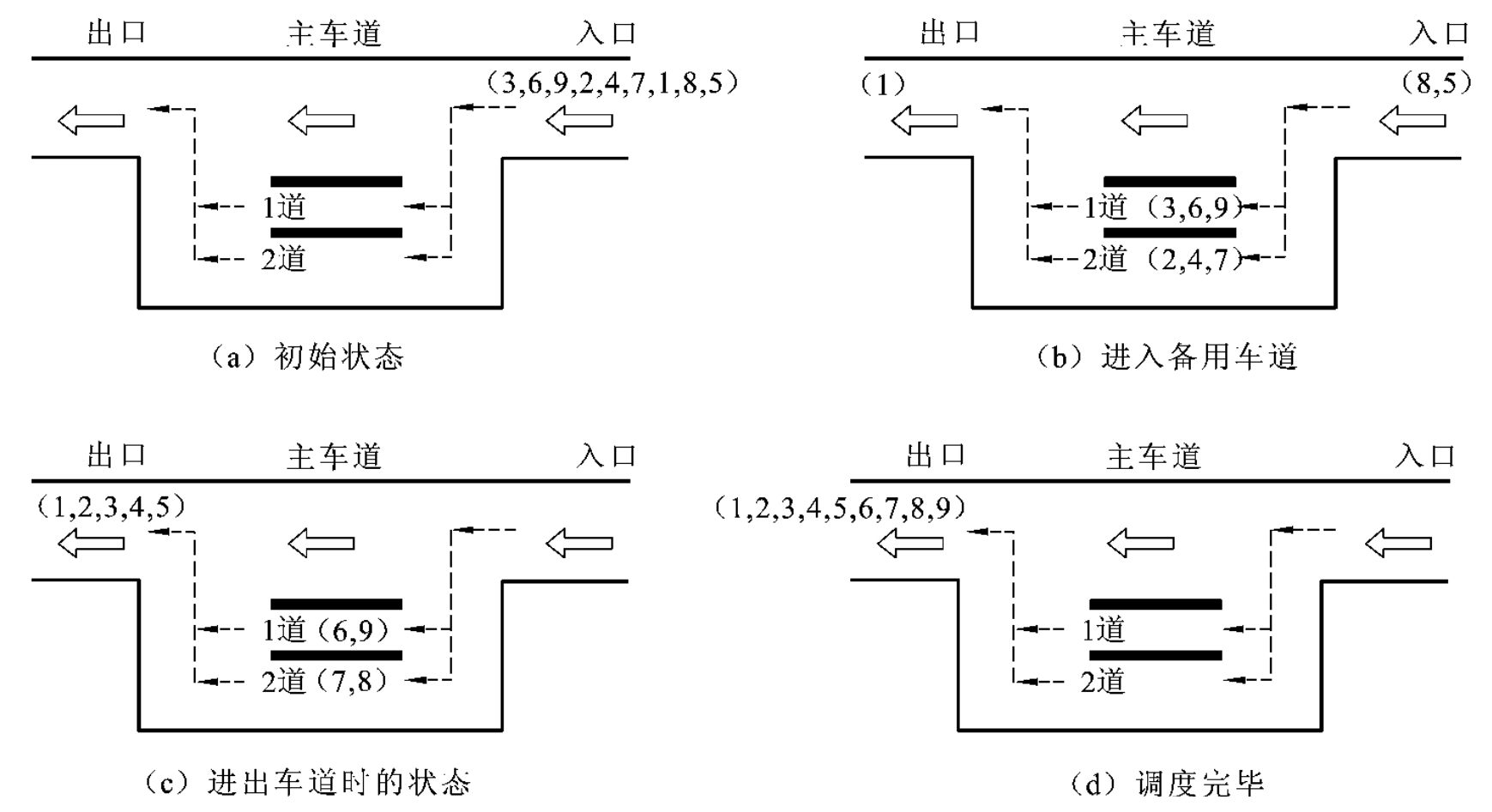
图3－15　2条备用车道的高度示例

若n号车进入第一备用车道用（c1＜－n）表示,n号车从第二备用道开出并开往出口用（n＜－c2）表示。则上述调度的操作序列可表示为:（c1＜－3）,（c1＜－6）,（c1＜－9）,（c2＜－2）,（c2＜－4）,（c2＜－7）,1号车开往出口,（2＜－c2）,（3＜－c1）,（4＜－c2）,（c2＜－8）,5号车开往出口,（6＜－c1）,（7＜－c2）,（8＜－c2）,（9＜－c1）。每个备用车道里的车辆都是严格按照先进先出的原则调度的。

值得注意的是,并不是所有调度问题都能使用2条备用车道就可以完成。例如,将上述序列改为（3,9,6,2,4,7,1,8,5）,则最少需要用3条备用车道才能完成。究竟需要多少条备用车道才能确保调度成功呢？最坏的情况是n辆车需要n－1条备用车道,也就是说当汽车开入的顺序和离去的顺序正好相反时,所用的备用车道的数目最多。

下面设计一个算法实现汽车调度功能。用一维数组表示n辆车的输入顺序,k为备用车道的数目,若调度成功则返回1,否则返回0。用链式队列作为备用车道的存储结构,h_i（i＝1,2,…,n）为第i条链队列的队首指针。用整型变量b记录进入出口的最大编号,初始时b＝0,表示尚无车到出口。算法依次从输入序列中取出下一个到达的车辆的编号num,如果num＝b＋1,num号汽车就直接驶往出口,并令b的值加1；否则依次检查k条备用车道,从中选出一条最适宜车道。所谓最适宜车道是指在最后一个车号小于num的所有非空车道中,选择最后车号最大的备用车道（否则会增加备用车道的数量）。如果所有非空备用车道的最后一个车号均大于num,就必须开辟一个新的备用车道作为最适宜车道。若已无空的备用车道的话,则调度失败,否则将num插入所选择的最适宜备用车道。如果num已到达出口,接下来应依次检查非空的备用车道,若该车道的队首车号p恰好等于b＋1,则删除队首元素p,将p送往出口,令b加1,直到各非空备用车道的队首车号大于b＋1或该车道为空。当输入结束且各备用车道也均为空时,调度结束,返回成功标志1,否则调度失败,返回0。

根据以上分析可得到一个完整的车辆调度算法。该算法由3个函数组成。其中,hold函数完成将num号车送入所选择的最适宜车道,即完成一辆车的调度；函数out（）完成输出,具体的工作是将各备用车道中满足送往出口条件的车号从备用车道中删除,直到每个备用车道为空或队首车号大于b＋1；函数cldu（）则调用函数hdd（）和函数out（）完成整个车辆的调度工作。

1.hold函数

【算法思想】　该算法完成将车号为num的车辆送入最适宜的车道的功能。若无最适宜的车道,则返回0,否则返回1。假设每个备用车道是一个链式队列,队列中元素最多为10个。所有头指针组成一个指针数组h。

具体算法如下。

2.out函数

【算法思想】　本算法完成将备用车道上所有满足条件的车辆按指定的顺序输出。

具体算法如下。

3.cldu函数

【算法思想】　使用k条备用车道,将存放在数组p中的n辆车的序列调度为按车号递增序列。

具体算法如下。

假设进入车道的汽车号序列事先存入数组x中,例如:int x＝（3,9,6,2,4,7,1,8,5）,则cldu（x,9,3）调度成功,而cldu（x,9,2）调度失败,说明最少应使用3条备用车道。

本章小结

1.栈是一种运算受到限制的特殊线性表,它仅允许在线性表的同一端作插入和删除操作。

2.队列也是一种运算受到限制的特殊线性表,它仅允许在线性表的一端进行插入操作,而在另一端进行删除操作。

3.队列的顺序存储一般采用循环队列形式,可以克服“虚溢出”的缺点,但最大的存储容量为循环队列容量减1。

4.队列的链式存储结构与单链表类似,但删除结点只能在表头,插入元素只能在表尾。

5.栈和队列的应用都很广泛。