树的定义和术语

6.1　树的定义和术语

本节先给出树（tree）的定义,然后介绍树的基本术语。

6.1.1　树的定义

1.树的定义

树是n（n≥0）个有限数据元素的集合。在任意一棵非空树T中,有以下一些特点。

（1）有且仅有一个特定的称为树根（root）的结点（根结点无前驱结点）。

（2）当n＞1时,除根结点之外的其余结点被分成m（m＞0）个互不相交的集合T₁,T₂,…,T_m。其中,每一个集合T_i（1≤i≤m）本身又是一棵树,并且称为根的子树。

树的定义采用了递归定义的方法,即在树的定义中又用到树的概念,这正好反映了树的固有特性。图6－1为树的结构示意图。

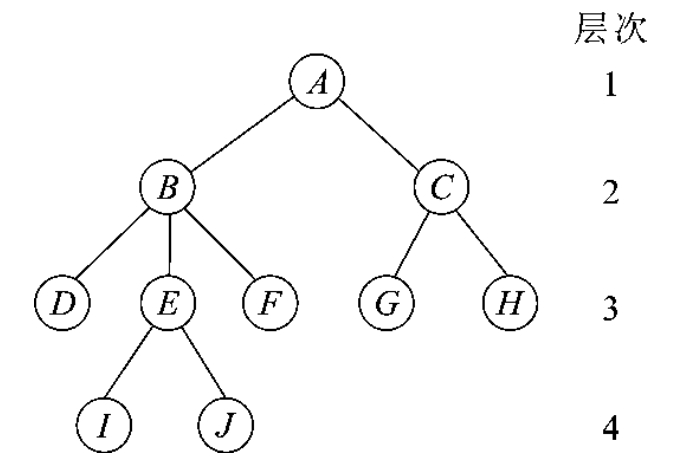
图6－1　树的结构示意图

2.树的其他表示法

图6－1所示是树结构的一种直观画法,其特点是对树的逻辑结构的描述非常直观、清晰,是使用最多的一种描述方法。除此以外,还有以下几种描述树的方法。

（1）嵌套集合法　嵌套集合法又称文氏图法,它是用集合的包含关系来描述树形结构,每个圆圈表示一个集合,套起来的圆圈表示包含关系。图6－1所示树的嵌套集合表示如图6－2（a）所示。

（2）圆括号表示法　圆括号表示法又称为广义表表示法,它是使用括号将集合层次与包含关系显示出来。图6－1所示树的圆括号表示法为:（A（B（D,E（I,J）,F）,C（G,H）））。

（3）凹入法　凹入法是用不同宽度的行来显示各结点,而行的凹入程度体现了各结点集合的包含关系,图6－1所示树的凹入法表示如图6－2（b）所示。树的凹入表示法主要用于树的屏幕显示和打印输出。

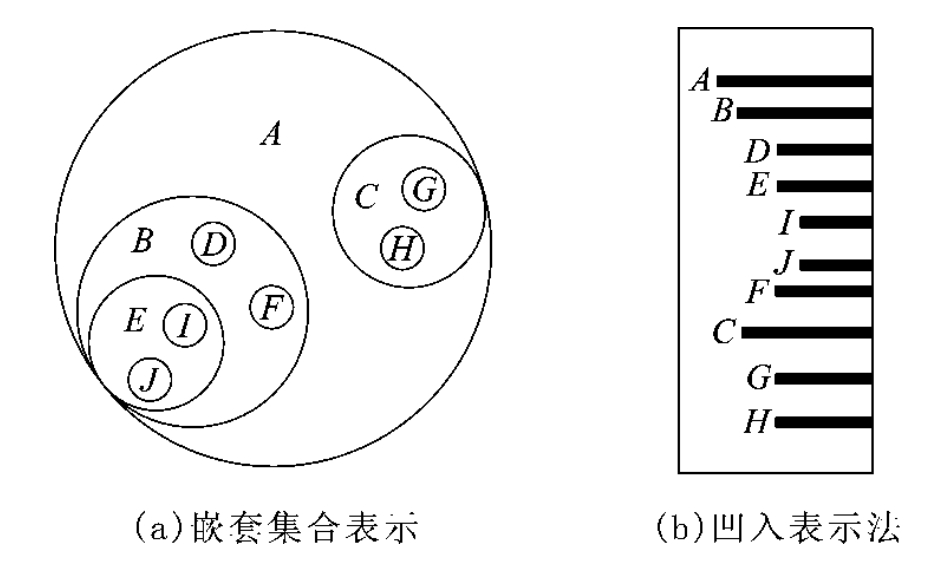
图6－2　树结构表示法

6.1.2　基本术语

树的基本术语主要有下列几种。

（1）结点:树的结点包含一个数据元素及若干指向其子树的分支。

（2）结点的度:结点所拥有的子树数称为该结点的度（degree）。

（3）树的度:树中各结点度的最大值称为该树的度。

（4）叶子（终端结点）:度为零的结点称为叶子结点。

（5）分支结点:度不为零的结点称为分支结点。

（6）兄弟结点:同一父亲结点下的子结点称为兄弟结点。

（7）层数:树的根结点的层数为1,其余结点的层数等于它双亲结点的层数加1。

（8）树的深度:树中结点的最大层数称为树的深度（或高度）。

（9）森林:零棵或有限棵互不相交的树的集合称为森林。

在数据结构中,树和森林并不像在自然界中那样有一个明显的量的差别。任何一棵树,只要删去根结点就成了森林,如图6－3所示。

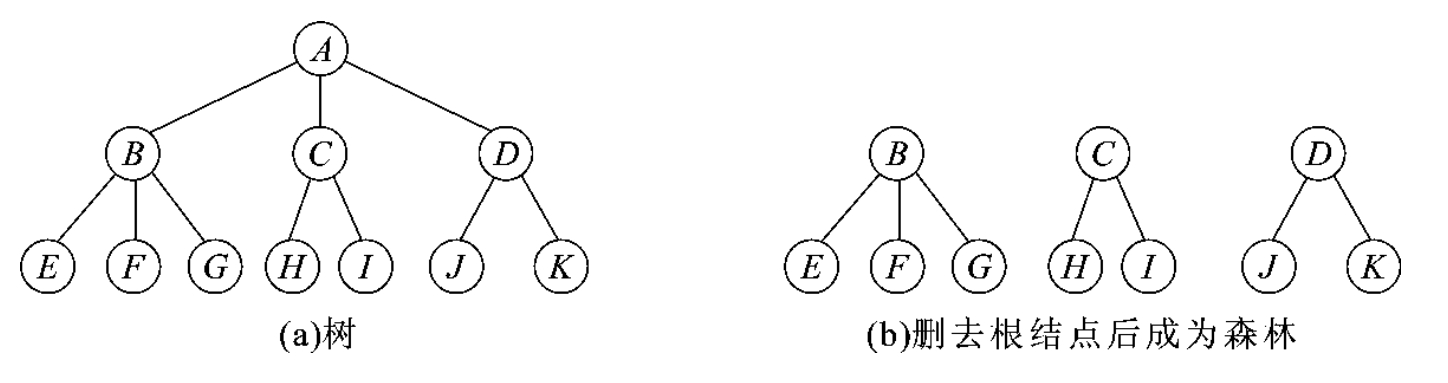
图6－3　树删去根结点后成为森林

（10）有序树和无序树:如果树中结点的各子树从左到右是有次序的（即不能互换）,则称这样的树为有序树；否则,称为无序树。