作用在挡土墙上的土压力

6　挡土墙

6.1　概述

挡土墙是防止土体坍塌的构筑物，其广泛应用于房屋建筑、水利、铁路、公路、港湾及桥梁等工程，比如支撑建筑物周围填土的挡土墙、地下室外墙和室外地下人防通道的侧墙、桥台及储藏粒状材料的挡墙等(如图6-1)。

图6-1　挡土墙的应用举例

挡土墙的土压力是指挡土墙后填土因自重或外荷载作用对墙背产生的侧向压力。严格来说，土压力的计算是比较复杂的，它不仅与土的性质、填土的过程和墙的刚度、形状等因素有关，还取决于墙的位移。如果挡土墙排水条件较差，或是岸边的挡土墙，还可能承受静水压力。若在挡土墙顶的地面上有公路或建有房屋等，则应考虑由于超载引起的附加应力。此外，建于地震区的挡土墙，还要考虑地震力所增加的土压力。土压力的计算有多种理论和方法，为简化计算，除了板桩墙外，一般假定墙是刚性的，并沿用朗肯和库仑的理论和计算方法。尽管这些理论都基于各种不同的理论和简化，但计算简便，且国内外大量挡土墙模型试验、原位观测及理论研究结果均表明其计算方法实用可靠。随着现代计算技术的提高，楔体试算法、“广义库仑理论”以及应用塑性理论的土压力解答等均得到了迅速发展，加筋土挡土墙设计理论亦日臻完善。

地基承载力是指地基单位面积上承受荷载的能力。为了保证地基在荷载作用下不至于出现整体剪切破坏而丧失其稳定性，在地基计算中必须验算地基的承载力。

6.2　作用在挡土墙上的土压力

6.2.1　土压力类型

影响土压力大小及分布的因素很多，其中最主要的因素为挡土墙的位移方向和位移量。根据挡土墙的位移情况和墙后土体所处的应力状态，土压力可以分为主动土压力、被动土压力、静止土压力三种。

(1) 主动土压力

当墙在土压力作用下产生向着离开土体方向的移动或绕墙根的转动时，墙后土体因侧面所受限制的放松而有下滑趋势，如图6-2(a)。为阻止其下滑，土体内潜在滑动面上的剪应力增加，从而使作用在墙背上的土压力减少。当墙的移动或转动达到某一数量时，滑动面上的剪应力等于土的抗剪强度，墙后土体达到主动极限平衡状态，发生一般为曲线形的滑动面，这时作用在墙上的土推力达到最小值，称为主动土压力Ea。

(2) 被动土压力

当墙在土压力作用下产生向着土体方向移动或绕墙根转动时，墙后土体受到挤压，有上滑趋势。为阻止其上滑，土体内剪应力反向增加，使作用在墙背上的土压力加大。直到墙的移动量足够大时，滑动面上的剪应力等于抗剪强度，墙后土体达到被动极限平衡状态，土体向上滑动，滑动面为曲面，如图6-2(b)，这时作用在墙上的土抗力达到最大值，称为被动土压力Ep。

(3) 静止土压力

当围护墙体有足够的截面，并且建立在坚实的地基上(如基岩)，墙在墙后土的推力作用下不产生任何移动或转动，如图6-2 (c)，墙后土体没有破坏，处于弹性平衡状态。这时，作用在围护墙背上的土压力称为静止土压力E0。

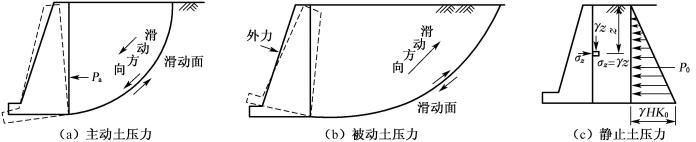
图6-2　三种土压力类型

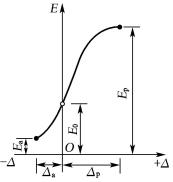
图6-3　土压力与墙身位移关系

土压力的影响因素主要有土的性质、挡土墙的位移方向、挡土墙和土的相对位移量、土体与墙之间的摩擦、挡土墙类型等。其中最重要的影响因素为挡土墙和土的相对位移。图6-3为三种土压力与挡土墙位移的关系。已有的试验研究也均表明：在相同条件下，主动土压力小于静止土压力，而静止土压力又小于被动土压力，即：

Ea<E0<Ep

产生被动土压力所需的位移量Δp大大超过产生主动土压力所需的位移量Δa，产生主动土压力和被动土压力所需位移量的参考值如表6-1所示。

表6-1　产生主动或被动土压力时所需挡土墙的位移量

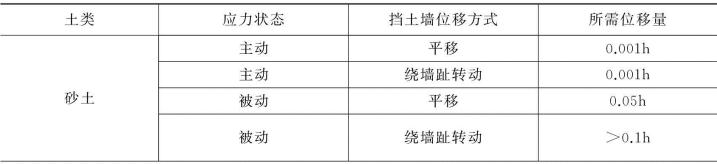
续表6-1

注：h为挡土墙高度。

6.2.2　静止土压力计算

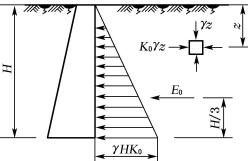
图6-4　静止土压力的分布

计算静止土压力时，挡土墙后的填土处于弹性平衡状态。如果假设填土是半无限弹性体，由于墙体静止不动，故土体无侧向位移，这时水平向静止土压力可按水平向自重应力公式计算(如图6-4)，即：

σ0=K0γz

(6-1)

式中:K0——静止土压力系数，或在自重应力计算中的土的静止侧向压力系数；

σ0——静止土压力强度(kPa)；

γ——填土的重度(kN/m3)；

z——计算点距离填土表面的深度(m)。

静止土压力系数K0与土的性质、密实程度等因素有关，对于砂土一般可取0.35～0.5，黏性土通常取0.5～0.7。对正常固结土，也可按下列半经验公式计算：

K0=1-sinφ′

(6-2)

式中:φ′——土的有效内摩擦角(°)。

也可以参照表6-2取值。

表6-2　静止土压力系数

表6-2为吴天行在《基础工程手册》一书中汇集的国外一些学者发表的有关静止土压力系数值。由表可以看出，虽然土类多样，但静止土压力系数变化不大，由式(6-2)可看出K0仅为φ′的函数，而与土的种类无关。一般砂土φ′=30°～40°，黏性土φ′=20°～35°。

由公式(6-1)可以看出，静止土压力沿墙高呈三角形分布(如图6-2(c)),如取单位墙长，则作用在墙上的静止土压力为：

(6-3)

式中：h——挡土墙墙高(m)。

合力E0的作用点在距离墙底h/3处。

6.3　朗肯土压力理论

6.3.1　基本概念

古典朗肯土压力理论是通过研究弹性半空间体内的应力状态，根据土的极限平衡条件得出的土压力计算方法。

图6-5(a)表示一表面为水平面的半空间，即土体向下和沿水平方向都伸展至无穷，在离地表z处取一单位微体M，当整个土体都处于静止状态时，各点都处于弹性平衡状态，设土体的重度为γ，显然M单元水平截面土的法向应力等于该处土的自重应力，即：

σz=γz

竖直截面上的法向应力为：

σx=K0γz

由于土体内每一竖直面都是对称面，因此竖直截面和水平截面上的剪应力都等于零，因而相应截面土的法向应力σz和σx都是主应力。

假设条件：墙顶土面水平，墙与土体间光滑，墙背与填土间无摩擦力产生，即无剪应力，墙背为主应力面。当挡土墙不出现位移处于静止状态时，墙后土体处于弹性平衡状态，作用在墙背上的应力状态与弹性半空间土体应力状态相同。在离填土面深度z处σz=σ1=γz，σx=σ3=K0γz。用σ1与σ3作出的莫尔应力圆与土的抗剪强度曲线不相切(图6-5(d)圆Ⅰ)。

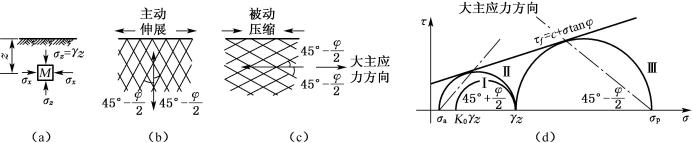
图6-5　半空间的极限平衡状态

设想由于某种原因将使整个土体在水平方向均匀地伸展或压缩，使土体由弹性平衡状态转为塑性平衡状态，如果土体在水平方向伸展，则M单元在水平截面上的法向应力σz不变而竖直面上的法向应力却逐渐减小，直至满足极限平衡条件为止(称为主动朗肯状态)，此时σx达最低限值σa。因此，σa是小主应力，而σz是大主应力，并且莫尔圆与抗剪强度包线相切，如图6-5(d)圆Ⅱ所示。若土体继续伸展，则只能造成塑性流动，而不至于改变其应力状态。反之，如果土体在水平方向压缩，那么σz仍保持不变而σx却不断增加，直到满足极限平衡条件(称为被动朗肯状态)时σx达最大限值σp，这时，σp是大主应力而σx是小主应力，莫尔圆为图6-5(d)中的圆Ⅲ。由于土体处于主动朗肯状态时大主应力所作用的面是水平面，故剪切破坏面与竖直面的夹角为45°-φ/2(图6-5(b))；当土体处于被动朗肯状态时，大主应力的作用面是竖直面，故剪切破坏面与水平面的夹角为45°-φ/2(图6-5(c))。因此，整个土体由互相平行的两簇剪切面组成。

朗肯将上述原理应用于挡土墙土压力计算中，设想用墙背直立的挡土墙代替半空间左边的土(图6-6)，如果墙背与土的接触面上满足剪应力为零的边界条件以及产生主动或被动朗肯状态的边界变形条件，则墙后土体的应力状态不变。由此可以推导出主动和被动土压力计算公式。

6.3.2　主动土压力

由土的强度理论可知，当土体中某点处于极限平衡状态时，大主应力σ1和小主应力σ3之间应满足以下关系式：

黏性土

(6-4)

或

(6-5)

无黏性土

(6-6)

或

(6-7)

对于如图6-5所示的挡土墙，设墙背光滑、直立、填土面水平。当挡土墙偏离土体时，由于墙后土体中离地表为任意深度z处的竖向应力σz=γz不变，亦即大主应力不变，而水平应力σx却逐渐减小直至产生主动朗肯状态，此时σx是小主应力σa，也就是主动土压力，由极限平衡条件式(6-5)和式(6-7)得：

无黏性土:

(6-8)

或

σa=γzKa

(6-9)

黏性土:

(6-10)

或

(6-11)

式中:Ka——主动土压力系数，；

γ——墙后填土的重度(kN/m3)，地下水位以下用有效重度；

c——填土的黏聚力(kPa)。

由公式(6-9)可知，无黏性土的主动土压力与z成正比，沿墙高压力呈三角形分布，如图6-6(b)所示，如取单位墙长计算，则主动土压力合力为：

(6-12)

或

(6-13)

Ea通过三角形形心，作用在离墙底H/3处。

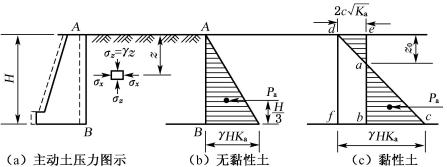
图6-6　朗肯主动土压力分布

由公式(6-11)可知，黏性土的主动土压力包括两部分：一部分是由土自重引起的土压力γzKa，另一部分是由黏聚力c引起的负侧压力，这两部分土压力叠加的结果如图6-6(c)所示，其中ade部分是负侧压力，对墙背是拉力，但实际上墙与土在很小的拉力下就会分离，故在计算土压力时这部分应略去不计，因此黏性土的土压力分布仅为abc部分。

a点离填土面的深度z0常称为临界深度，在填土面无荷载的条件下，可令式(6-11)为零，求得z0值，即：

得临界深度：

(6-14)

如取单位墙长计算，则主动土压力合力Ea为：

将式(6-14)代入上式后可得：

(6-15)

Ea通过三角形压力分布图abc的形心，即作用在离墙底(H-z0)/3处。

6.3.3　被动土压力

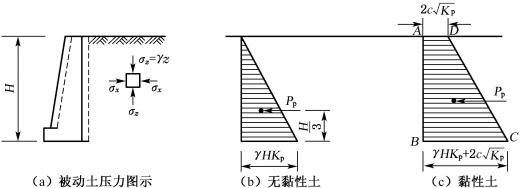
图6-7　朗肯被动土压力分析

当墙受到外力作用而推向土体时(图6-7(a))，墙土中任意一点的竖向应力σz=γz仍不变，而水平向应力σx却逐渐增大，直至出现被动朗肯状态，此时σx已达最大限值σp，因此σp是大主应力，也就是被动土压力，而σz则是小主应力，于是由式(6-4)和式(6-6)可得：

无黏性土:

σp=γzKp

(6-16)

黏性土:

(6-17)

式中:Kp——被动土压力系数，。

由式(6-16)和式(6-17)可知，无黏性土的被动土压力呈三角形分布(图6-7(b))，黏性土的被动土压力则呈梯形分布(图6-7(c))。如取单位墙长计算，则被动土压力合力Ep可由下式计算：

无黏性土

(6-18)

黏性土

(6-19)

被动土压力Ep通过三角形或梯形压力分布图的形心，可通过一次求矩得到。

【例6-1】　已知某挡土墙，墙高5.0m，墙背直立、光滑，填土面水平。填土的物理力学性质指标如下：c=10.0kPa，φ=20°，γ=18.0kN/m3。试求主动土压力合力及其作用点，并绘出主动土压力强度分布图。

【解】　墙背竖直光滑，填土面水平，满足朗肯条件，所以可以按照式(6-11)计算沿墙高的土压力强度。

故地面处　

墙底处　=30.10kPa

因填土为黏性土，故须计算临界深度z0，由公式(6-14)可得：

图6-8　例6-1主动土压力分布图

可绘制土压力分布图如图6-8所示，其总主动土压力为：

=51.4kN/m

主动土压力Ea的作用点离墙底的距离为：

6.3.4　其他几种情况下的土压力计算

1)填土表面有连续的均布荷载

当挡土墙后填土表面有连续均布荷载q作用时，一般可将均布荷载换算成位于地表以上的当量土重，即用假想的土重代替均布荷载。当填土面水平时，当量的土层厚度h′为：

(6-20)

图6-9　填土表面有连续均布荷载

如图6-9所示，再以h+h′为墙高，按填土面无荷载情况计算土压力。如果填土为无黏性土时，墙顶a点的土压力强度为：

σaa=γh′Ka=qKa

墙底b点的土压力强度为：

σab=γ(h+h′)Ka=(q+γh)Ka

压力分布如图6-9所示，实际的土压力分布为梯形abcd部分，土压力作用点在梯形的重心。

因此，当填土面有均布荷载时，其土压力强度只是比在无荷载情况时增加一项qKa即可。对于黏性填土情况也是一样。

2) 填土表面受局部均布荷载

当填土表面承受有局部均布荷载时，荷载对墙背的土压力强度附加值仍为qKa，但其分布范围很难从理论上严格规定。通常可采用近似方法处理，即从局部均布荷载的两端点a和b各作一条直线，其与水平表面成45°+φ/2角，与墙背相交于 c点和d点，则墙背cd段范围内受到qKa的作用，故作用于墙背的土压力分布如图6-10所示。

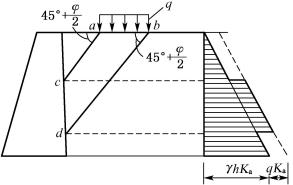
图6-10　填土表面有局部均布荷载

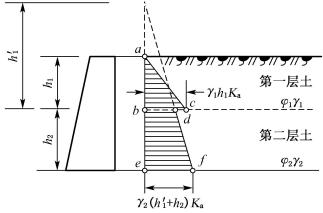
图6-11　墙后填土成层

3) 成层填土

如图6-11所示，当墙后填土有几种不同种类的水平土层时，第一层土压力按均质土计算。计算第二层土压力时，将上层土按重度换算成与第二层重度相同的当量土层计算，当量土层厚度=h1γ1/γ2，以下各层亦同样计算。由于土的性质不同，各层土的土压力系数也不同。现以黏性土主动土压力计算为例:

第一层填土的土压力强度为：

第二层填土的土压力强度为：

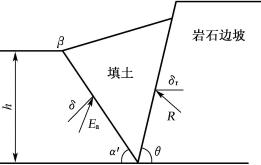
图6-12　有限填土的土压力计算

对于无黏性土，只需令上述各式中c1=c2=0即可。此外尚需注意，在两土层交界处因各土层土质指标不同，其土压力大小亦不同，故此时土压力强度曲线将出现突变。

4) 有限填土的土压力计算

如图6-12所示，当支挡结构后缘存在较陡峭的稳定岩石坡面，岩坡的坡角时，应按有限范围填土计算墙背土压力，取岩石坡面为破裂面。根据稳定岩石坡面与填土间的摩擦角，按下式计算主动土压力系数：

(6-21)

式中:θ——稳定岩石坡面的倾角；

δr——稳定岩石坡面与填土间的摩擦角，按试验确定，当无试验资料时，可取δr=0.33φk，φk为填土的内摩擦角标准值。

5) 墙后填土有地下水

墙后填土常会部分或全部处于地下水位以下，由于渗水或排水不畅会导致墙后填土含水量增加。工程上一般可忽略水对砂土抗剪强度指标的影响，但对于黏性土，随着含水量的增加，抗剪强度指标明显降低，导致墙背土压力增大。因此，挡土墙应具有良好的排水措施，对于重要工程，计算时还应考虑适当降低抗剪强度指标c和φ值。此外，地下水位以下土的重度应取浮重度，并计入地下水对挡土墙产生的静水压力γwh2(如图6-13)的影响。因此，作用在墙背上总的侧压力为土压力和水压力之和。图6-13中abdec为土压力分布图，而cef为水压力分布图。

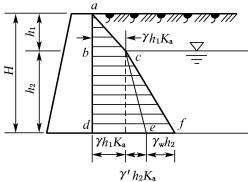
图6-13　填土中有地下水

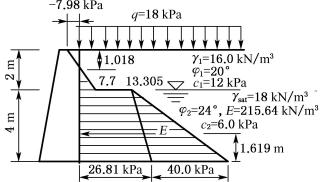
图6-14　例6-2土压力分布

【例6-2】　某挡土墙，墙高6m，墙背竖直、光滑，墙后填土面水平，并作用有均布荷载q=18kPa，各填土层物理力学性质指标如图6-14所示。试计算该挡土墙墙背总侧压力E及其作用点位置，并绘出侧压力分布图。

【解】　墙背竖直、光滑，填土面水平，符合朗肯条件。首先计算第一层填土的土压力强度为:

=7.70kPa

第二层填土的土压力强度：

=13.305kPa

=26.81kPa

第二层底部水压力强度　σw=γwh2=10×4=40.00kPa

假设临界深度为z0则　

代入数据为　

解得

z0=1.018m

各点的土压力强度绘于图6-14，可见其总侧压力为：

×(40+26.81-13.305)×4

=3.78+53.22+107.01=164.01kN/m

总侧压力E至墙底的距离x为：

6.4　库仑土压力理论

6.4.1　基本假定

自库仑土压力理论提出至今，已有200多年的历史，但在工程界仍得到广泛的应用。库仑土压力理论是根据墙后土体处于极限平衡状态并形成一滑动楔体时，从楔体的静力平衡条件得出的，其基本假定为：①墙后土体为均质各向同性的理想散体(无黏性土)；②挡土墙很长，属平面变形问题；③滑动破坏面为一平面。

库仑土压力理论适用于砂土或碎石填料的挡土墙计算，可考虑墙背倾斜、填土面倾斜以及墙背与填土间的摩擦等多种因素的影响。分析时，一般沿墙长方向取1m考虑。

6.4.2　主动土压力

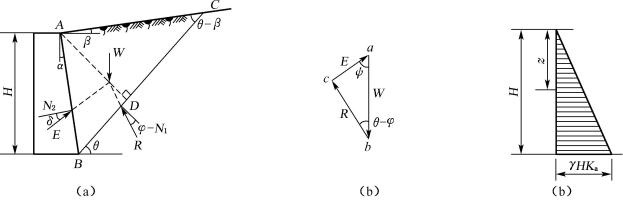
图6-15　库仑主动土压力计算图

如图6-15(a)所示，当墙向前移动或转动而使墙后土体沿某一破裂面破坏时，移动后如虚线所示，土楔ABC向下滑动而处于主动极限平衡状态。取ABC为脱离体，研究其力的平衡条件，则土楔的平衡决定于3个力，分别是土楔自重、BC面及AB面的反力。土楔自重为W，方向垂直向下，大小由ABC面积乘以土楔的容重；滑裂面BC上作用反力R，R由两部分组成，一是W在BC面法向上的分力N，二是由于N的作用，当土楔下滑时产生的摩阻力，由于N决定于W，因此，R的方向已知，大小随W而变化。AB面的反力即为土压力E，E与墙背法线的夹角等于墙土间的摩擦角δ。土楔所受的力组成的力多边形为一封闭的三角形，如图6-15(b)所示。

(1) 重力W：由土楔体ABC引起，根据几何关系可得：

在△ABC中，利用正弦定理可得：

其中

带入得：

(2) 反力R：为破裂面BC上土楔体重力的法向分力与该面土体间的摩擦力的合力，其作用于BC面上，与BC面法线的夹角等于土的内摩擦角φ。当楔体下滑时，位于法线下侧。

(3) 墙背反力E：其与墙背AB法线的夹角等于土与墙体材料之间的外摩擦角δ，该力与作用在墙背上的土压力大小相等，方向相反。当楔体下滑时，该力位于法线的下侧。

土楔体ABC在上述三力作用下处于静力平衡状态，因此土楔所受的力组成的力多边形为一封闭的三角形，该三角形中所有内角已知，当土楔重量W已知时，则一边长已知，由正弦定理可得：

(6-22)

式中　

上式中的H、φ、α、γ、β、δ均为已知，滑动面BC与水平面的夹角θ为任意假定的。因此，选定不同的θ角，可得到一系列相应的土压力E值，因此E为θ的函数。而E的最大值Emax即为墙背的主动土压力，其对应的滑动面即是土楔最危险滑动面。因此，可以利用微分学中求极值的方法求得E的极大值，即：

求解得到当E为极大值时填土的破坏角θcr为：

式中

将θcr代入式(6-22)，经整理后可得库仑主动土压力的一般表达式为：

(6-23)

式中

(6-24)

其中：Ka——库仑主动土压力系数；

δ——土与墙背材料间的外摩擦角(°)；

β——墙后填土面的倾角(°)；

α——墙背与竖直线的夹角(°)，俯斜时取正号，仰斜时取负号。

当墙背竖直(α=0)、光滑(δ=0)、填土面水平(β=0)时，式(6-24)变为：

在这种条件下，库仑公式与朗肯公式完全相同。因此，朗肯理论是库仑理论的特殊情况。

沿墙高的土压力分布强度σa，可通过Ea对z取导数而得到：

(6-25)

由此可见，主动土压力分布强度沿墙高呈三角形线性分布(图6-15(c))，土压力合力的作用点离墙底H/3处，方向与墙面的法线成δ角。另外需要注意，图6-15(c)中土压力分布图只表示其数值大小，而不代表其作用方向。

6.4.3　被动土压力

当挡土墙在外力作用下挤压土体(图6-16(a))，楔体沿破裂面向上隆起而处于极限平衡状态时，同理可得作用在楔体上的力三角形如图6-16(b)所示。此时由于楔体上隆，E和R均位于法线的上侧。按求主动土压力相同的方法可求得被动土压力Ep的库仑公式为：

(6-26)

式中

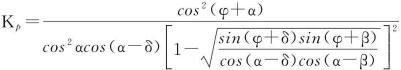
(6-27)

其中：Kp——被动土压力系数。

若墙背竖直(α=0)、光滑(δ=0)及墙后填土面水平(β=0)，则式(6-27)变为：

即与无黏性土的朗肯公式相同。被动土压力强度可按下式计算：

(6-28)

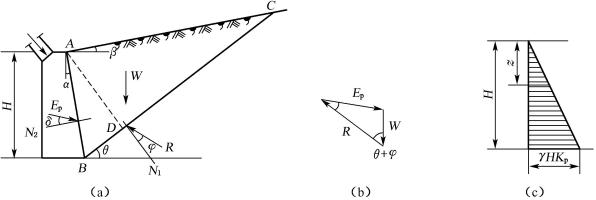
图6-16　库仑被动土压力计算图

被动土压力强度沿墙高也呈三角形分布(图6-16(c))，其合力作用点在距墙底H/3处。研究发现，在被动状态库仑理论假定的平面滑裂与实际情况差异较大，一般计算的被动土压力偏大，并且其误差随着δ角的加大而增加。

6.4.4　黏性土的库仑土压力理论

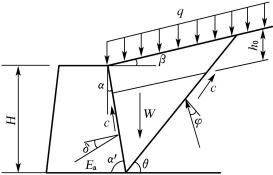
图6-17　挡土墙的一般计算图示

库仑土压力理论假设墙后填土是理想的散体，从理论上说只适用于无黏性填土，没有考虑黏性土的黏聚力c，但在实际工程中经常采用黏性土作为填料。为了考虑黏性土的黏聚力c对土压力的影响，在应用库仑理论时，常采用所谓的“等代内摩擦角φD”来进行计算。

常见的等代内摩擦角换算方法有：①根据经验一般黏性土取φD=30°～35°；②根据土的抗剪强度相等的原则；③与朗肯土压力相等；④与朗肯土压力的力矩相等。但在使用过程中发现该方法误差较大，在低墙时偏于保守，高墙时偏于危险。因此，近年来很多学者在库仑理论的基础上，计入了墙后填土面超载、填土黏聚力、填土与墙背间的粘结力以及填土表面附近的裂缝深度等因素(如图6-17)的影响，提出了所谓的“广义库仑理论”。根据图6-17所示计算图示，可导得主动土压力系数Ka如下：

kq+2k2cosφsinψ

(6-29)

式中

；

；　；

；　；　；

；

G2=kqcos(α-β)sin(φ-β)+k2cosφ；　ψ=α+δ+φ-β

其中：q——填土表面均布荷载(kPa)；

h0——地表裂缝深度(m)；

c——填土的黏聚力(kPa)；

c′——墙背与填土间的粘结力(kPa)。

其他符号意义同前。显然，若在上式中令c=0、q=0及c′=0，整理后可得式(6-24)。

6.4.5　《建筑地基基础设计规范》推荐的公式

《建筑地基基础设计规范》(GB 50007—2011)推荐采用上述所谓“广义库仑理论”解答，但不计地表裂缝深度h0及墙背与填土间的粘结力c′，即在公式(6-29)中令h0=0，c′=0，并注意到此时墙背倾角α=90°-α′(图6-17)，从而可得：

+2ηsinα′cosφcos(α′+β-φ-δ)-2·

其中

；　

其他符号意义同前。

6.4.6　楔体试算法

楔体试算法是一种图解或数解法，可用于黏性填土及填土面形状不规则，并作用有集中荷载或均布荷载的情况。

该法以作用在任一破坏楔体上的力多边形为依据。如图6-18所示，墙背与填土间的黏聚力Cw=bd×c′，Cs=bh4×c，地表裂缝深度，当计算被动土压力时，h0=0。由力多边形可得主动土压力：

(6-30)

被动土压力：

(6-31)

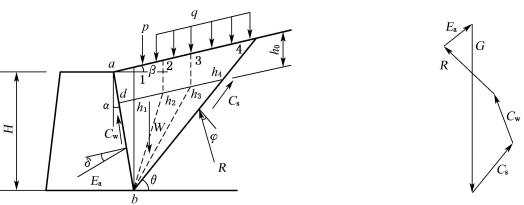
图6-18　黏性填土的楔体试算法

具体计算步骤如下：

(1) 按比例绘出挡土墙及地表轮廓线，并计算地表裂缝深度。

(2) 将墙后土体分成若干楔体，如abh11，abh22，…，并计算相应的楔体自重W1，W2，…。

(3) 计算Cw和Cs，一般当混凝土与土相接触时c′=0.67c；土与土相接触c′=c；若不计墙背粘结力，则c′=0。

(4) 按式(6-30)或式(6-31)计算相应的Ea1(或Ep1)，Ea2(或Ep2)，…。

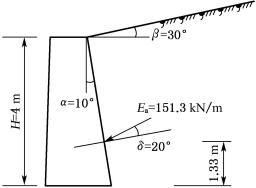
图6-19　例6-3图示

(5) 比较各Eai(Epi)，取其最大(小)值即为所求的主(被)动土压力设计值Ea(Ep)。

【例6-3】　挡土墙高4m，墙背倾斜角α=10°，填土坡角β=30°，填土重度γ=18kN/m3，φ=30°，c=0，填土与墙背的摩擦角δ=20°，如图6-19所示。试按库仑理论求主动土压力Ea及其作用点。

【解】　根据δ=20°，α=10°，β=30°，φ=30°，查表得库仑主动土压力系数Ka=1.051，得主动土压力为：

×18×42×1.051=151.3kN/m

主动土压力作用点距离墙底：=1.33m

6.4.7　土压力计算的几个应用问题

1) 朗肯理论与库仑理论的比较

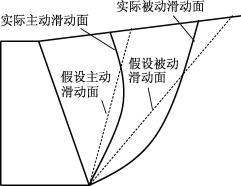
图6-20　假设滑动面与实际滑动面比较

朗肯土压力理论概念明确，公式简单，便于记忆，可用于黏性填土和无黏性填土，在工程中应用广泛。但必须假定墙背竖直、光滑、填土面水平，使计算条件和适用范围受到限制，并由于该理论忽略了墙背与填土之间的摩擦影响，使计算的主动土压力值偏大，被动土压力值偏小，结果偏于安全。

库仑土压力理论假设墙后填土破坏时破坏面为一平面，而实际为一曲面。实践证明，只有当墙背倾角α及墙背与填土间的外摩擦角δ较小时，主动土压力的破坏面才接近于平面，因此计算结果存在一定的偏差。通常，在计算主动土压力时偏差为2%～10%，基本能满足工程精度要求；但计算被动土压力时，由于破裂面接近于对数螺线，计算结果误差较大，有时可达2～3倍甚至更大(如图6-20)。因此，宜按有限差分解或考虑对数螺线区的塑性理论解计算，具体方法可参见有关文献。

2) 挡土墙位移大小与方式

实际工程中，挡土墙位移的大小和方式影响着墙背土压力的大小与分布。若墙的下端不动，上端外移，墙背压力将按直线分布，总压力作用点位于墙底以上H/3处，当上端外移达到某一限值时，墙背填土发生主动破坏，墙背呈现主动土压力。若墙的上端不动，下端外移，则位移的大小不能使墙背填土发生主动破坏，压力为曲线分布，总压力作用点位于墙底以上约H/2处。当墙的上端和下端都向外移动时，若位移大小未使土体达主动破坏，此时压力为曲线分布，总压力作用点位于墙底以上约H/2处；若位移超过某一限值，则填土发生主动破坏，压力为直线分布，总压力作用点将降至墙高1/3处。

3) 土体抗剪强度指标

填土抗剪强度指标的确定极为复杂，必须考虑挡土墙在长期工作下墙后填土状态的变化及长期强度的下降因素，方能保证挡土墙的安全。根据国外研究成果，此数值为标准抗剪强度的1/3左右。有的规定土的计算摩擦角为标准值减去2°，黏聚力为标准值的3/10～2/5。大量调查表明，该计算值与实际情况比较相符。

4) 墙背与填土的外摩擦角δ

δ的取值大小对计算结果影响较大。根据计算，当墙背为砂性填土，δ从0°提高到15°时，挡土墙的圬工体积可减小15%～20%。其取值大小取决于墙背的粗糙程度、填土类别以及墙背的排水条件等。墙背愈粗糙，填土的φk值愈大，则δ也愈大。此外，δ还与超载大小及填土面的倾角β成正比。一般δ在0～φ之间，如表6-3所示。

表6-3　土对挡土墙墙背的外摩擦角δ

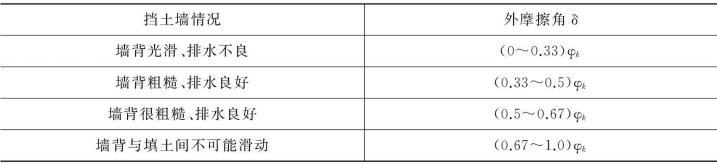
注：φk为墙背填土的内摩擦角标准值。

6.5　挡土墙的类型

挡土墙的种类繁多，因此挡土墙类型的划分方法也较多，除按挡土墙设置位置划分外，还可按结构形式、建筑材料、施工方法及所处环境条件等进行划分。如按建筑材料可分为石、混凝土及钢筋混凝土挡土墙等；按所处环境条件可分为一般地区挡土墙、浸水地区挡土墙与地震地区挡土墙等。

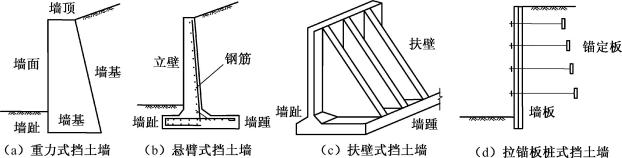
图6-21　常见挡土墙类型

一般以挡土墙的结构形式分类为主，常见的挡土墙形式有重力式(图6-21(a))、悬臂式(图6-21(b))、扶壁式(图6-21(c))、锚杆、锚定板式挡土墙(图6-21(d))，此外，还有竖向预应力锚杆式、土钉式及桩板式(图6-22)。各类挡土墙的适用范围取决于墙趾地形、工程地质、水文地质、建筑材料、墙的用途、施工方法、技术经济条件及当地的经验等因素。

挡土墙类型的选择应根据支挡填土或土体求得稳定平衡的需要，研究荷载的大小和方向、基础埋置的深度、地形地质条件、与既有建筑物平顺衔接、容许的不均匀沉降、可能的地震作用、墙壁的外观、环保的特殊要求、施工的难易和工程造价，综合比较后确定。

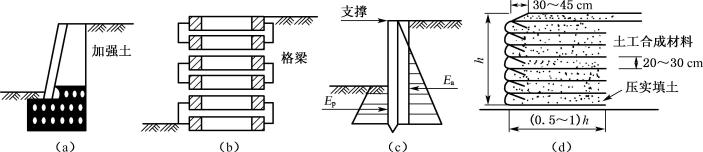
图6-22　其他各种形式的挡土结构

6.6　重力式挡土墙

重力式挡土墙是以挡土墙自身重力来维持挡土墙在土压力作用下的稳定，是我国目前常用的一种挡土墙。重力式挡土墙可用块石、片石、混凝土预制块作为砌体，或采用片石混凝土、混凝土进行整体浇筑。半重力式挡土墙可采用混凝土或少筋混凝土浇筑。重力式挡土墙可用石砌或混凝土建成，一般做成简单的梯形。优点是结构简单，就地取材，施工方便，经济效果好。所以，重力式挡土墙在我国铁路、公路、水利、港湾、矿山等工程中得到广泛的应用。

6.6.1　重力式挡土墙类型

重力式挡土墙可根据其墙背的坡度分为仰斜、俯斜、垂直三种类型(图6-23)。墙基的前缘称为墙趾，后缘称为墙踵。按土压力理论，仰斜墙背的主动土压力最小，而俯斜墙背的主动土压力最大，垂直墙背位于两者之间。如挡土墙修建时需要开挖，因仰斜墙背可与开挖的临时边坡相结合，而俯斜墙背后需要回填土，因此，对于支挡挖方工程的边坡，以仰斜墙背为好。反之，如果是填方工程，则宜用俯斜墙背或垂直墙背，以便填土易夯实。在个别情况下，为减小土压力，采用仰斜墙也是可行的，但应注意墙背附近的回填土质量。当墙前原有地形比较平坦，用仰斜墙比较合理；若原有地形较陡，用仰斜墙会使墙身增高很多，此时宜采用垂直墙或俯斜墙。

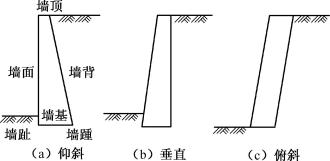
图6-23　重力式挡土墙形式

图6-24　几种特殊重力式挡土墙

为减小作用在挡土墙墙背上的主动土压力，除了采用上述仰斜式挡土墙外还可以选择衡重式挡土墙(图6-24(a))。这种挡土墙的墙背型式有利于减小主动土压力、增大抗倾覆能力，因而应用甚多。此外，还可以采用图6-24(b)所示的减压平台。减压平台一般设在墙背中部附近并向后伸出，最好伸到滑动面附近。减压平台以下部分墙背所受的土压力仅与台下填土的重量有关。当挡土墙的抗滑稳定性不能满足设计要求时，可考虑将基底做成逆坡；为了减小基底压力，还可以加墙趾台阶，这样也有利于墙的抗倾覆稳定(图6-24(c))。

6.6.2　重力式挡土墙类型的选择

选择合理的挡土墙墙型，对挡土墙的设计具有重要意义。

1) 使墙后土压力最小

6.6.1节已经介绍过，重力式挡土墙按墙背的倾斜情况分为仰斜、垂直和俯斜三种。仰斜墙主动土压力最小，俯斜墙被动土压力最大，垂直墙主动土压力处于仰斜和俯斜之间，因此仰斜墙较为合理，墙身截面设计较为经济，应优先考虑应用。在进行墙背的倾斜型式选择时，还应根据使用要求、地形条件和施工等情况综合考虑确定。

2) 墙的背坡和面坡的选择

在墙前地面坡度较陡处，墙面坡可取1∶0.05～1∶0.2，也可采用直立的截面。当墙前地形较平坦时，对于中、高挡土墙，墙面坡可用较缓坡度，但不宜缓于1∶0.4，以免增高墙身或增加开挖宽度。仰斜墙墙背坡愈缓，则主动土压力愈小。但为了避免施工困难，墙背仰斜时其倾斜度一般不宜缓于1∶0.25，面坡应尽量与背坡平行(图6-25)。

3) 基底逆坡坡度

在墙体稳定性验算中，倾覆稳定较易满足要求，而滑动稳定常不易满足要求。为了增加墙身的抗滑稳定性，将基底做成逆坡是一种有效的办法(图6-26)。对于土质地基的基底逆坡一般不宜大于0.1∶1(n∶1)。对于岩石地基一般不宜大于0.2∶1。由于基底倾斜，会使基底承载力减少，因此需将地基承载力特征值折减。当基底逆坡为0.1∶1时，折减系数为0.9；当基底逆坡为0.2∶1时，折减系数为0.8。

图6-25　面坡与背坡平行

图6-26　基底逆坡

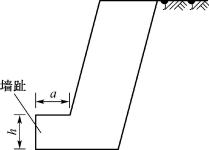
图6-27　墙趾台阶

4) 墙趾台阶

当墙身高度超过一定限度时，基底压应力往往是控制截面尺寸的重要因素。为了使基底压应力不超过地基承载力，可加墙趾台阶(图6-27)，以扩大基底宽度，这对挡土墙的抗倾覆和滑动稳定都是有利的。

墙趾高h和墙趾宽a的比例可取h∶a=2∶1。a不得小于20cm。墙趾台阶的夹角一般应保持直角或钝角，若为锐角时不宜小于60°。此外，基底法向反力的偏心距必须满足e≤0.25b(b为无台阶时的基底宽度)。

6.6.3　重力式挡土墙的构造

1) 挡土墙的埋置深度

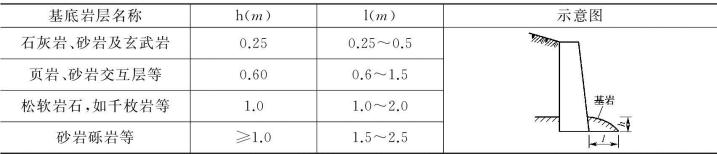
挡土墙的埋置深度(如基底倾斜，则按最浅的墙趾处计算)，应根据持力层地基土的承载力、冻结因素确定。土质地基一般不小于0.5m。若基底土为软弱土层时，则按实际情况将基础尺寸加深加宽，或采用换土、桩基或其他人工地基等，如基底层为岩石、大块碎石、砾砂、粗砂、中砂等，则挡土墙基础埋置深度与冻土层深度无关(一般挡土墙基础埋置在冻土层以下0.25m处)；若基底为风化岩层时，除应将其全部清除外，一般应加挖0.15～0.25m。如基底为基岩，则挡土墙嵌入岩层的尺寸应不小于表6-4的规定。

表6-4　挡土墙基础嵌入岩层尺寸表

2) 墙身构造

挡土墙各部分的构造必须符合强度和稳定的要求，并根据就地取材、经济合理、施工方便、按地质地形等条件确定。一般块石挡土墙顶宽不应小于0.4m。

3) 排水措施

雨季时节，雨水沿坡下流。如果在设计挡土墙时没有考虑排水措施或因排水不良，就将使墙后土体的抗剪强度降低，导致土压力的增加。此外，由于墙背积水，又增加了水压力。这是造成挡土墙倒塌的主要原因。

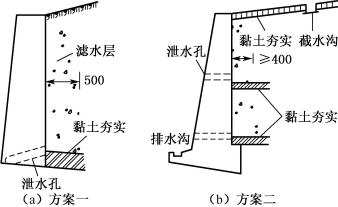
图6-28　挡土墙的排水措施

为了使墙后积水易于排出，通常在墙身布置适当数量的泄水孔，图6-28为两个排水较好的方案。泄水孔的尺寸根据排水量而定，可分别采用50mm×100mm、100mm×100mm、150mm×200mm的矩形孔，或采用50～100mm的圆孔。孔眼间距为2～3m。若挡土墙高度大于12m，则应根据不同高度加设泄水孔。当墙后渗水量较大，为了减少动水压力对墙身的影响，应增密泄水孔，加大泄水孔尺寸或增设纵向排水措施。在泄水孔附近应用卵石、碎石或块石材料覆盖，做滤水层，以防泥砂淤塞。为了防止墙后积水渗入地基，应在最低泄水孔下部铺设黏土层并夯实，并设散水或排水沟，如图6-28所示。

4) 填土质量要求

选择质量好的填料以及保证填土的密实度是挡土墙施工的两个关键问题。根据土压力理论进行分析，为了使作用在挡土墙上的土压力最小，应该选择抗剪强度高、性质稳定、透水性好的粗颗粒材料作填料，例如卵石、砾石、粗砂、中砂等，并要求这些材料含泥量小。如果施工质量得到保证，填料的内摩擦力大，对挡土墙产生的主动土压力就较小。

在工程上实际的回填土往往含有黏性土，这时应适当混入碎石，以便易于夯实和提高其抗剪强度。对于重要的、高度较大的挡土墙，用黏性土作回填土料是不合适的，因为黏性土遇水体积会膨胀，干燥时又会收缩，性质不稳定，由于交错膨胀与收缩可在挡土墙上产生较大的侧应力，这种侧应力在设计中是无法考虑的，因此会使挡土墙遭到破坏。

不能用的回填土为淤泥、耕植土、成块的硬黏土和膨胀性黏土，回填土中还不应夹杂有大的冻结土块、木块和其他杂物，因为这类土产生的土压力大，对挡土墙的稳定极为不利。

对于常用的砖、石挡土墙，当砌筑的砂浆达到强度的70%时方可回填，回填土应分层夯实。

5) 沉降缝和伸缩缝

由于墙高、墙后土压力及地基压缩性的差异，挡土墙宜设置沉降缝；为了避免因混凝土及砖石砌体的收缩硬化和温度变化等作用引起的破裂，挡土墙宜设置伸缩缝。沉降缝与伸缩缝实际上是同时设置的，可把沉降缝兼作伸缩缝，一般每隔10～20m设置一道，缝宽约2cm，缝内嵌填柔性防水材料。

6) 挡土墙的材料要求

石料：石料应经过挑选，在力学性质、颗粒大小和新鲜程度等方面要求一致，不应有过分破碎、风化外壳或严重的裂缝。

砂浆：挡土墙应采用水泥砂浆，只有在特殊条件下才采用水泥石灰砂浆、水泥黏土砂浆和石灰砂浆等。在选择砂浆强度等级时，除应满足墙身计算所需的砂浆强度等级外，在构造上还应符合有关规则要求。在9度地震区，砂浆强度等级应比计算结果提高一级。

7) 挡土墙的砌筑质量

挡土墙施工必须重视墙体砌筑质量。挡土墙基础若置于岩层上，应将岩层表面风化部分清除。条石砌筑的挡土墙，多采用一顺一丁砌筑方法，上下错缝，也有少数采用全丁全顺相互交替的做法，一般应该保证搭缝良好，砌稳安正。采用毛石砌筑的挡土墙，除尽量采用石块自然形状，保证各轮丁顺交替、上下错缝的砌法外，还要严格保证砂浆水灰比符合要求、填缝紧密、灰浆饱满，确保每一块石料安稳砌正，墙体稳固。砌料应紧靠基坑侧壁，使之与岩层结成整体，待砌浆强度达到70%以上时方可进行墙后填土。

在松散坡积层地段修筑挡土墙，不宜整段开挖，以免在墙完工前土体滑下；宜采用马口分段开挖方式，即跳槽间隔分段开挖。施工前应先做好地面排水。

6.6.4　重力式挡土墙的计算

挡土墙的设计计算应根据使用过程中可能出现的荷载，按承载力极限状态和正常使用极限状态进行荷载效应组合，并取最不利组合进行设计。截面尺寸一般按试算法确定，即先根据挡土墙的工程地质条件、填土性质以及墙身材料和施工条件等凭经验初步拟定截面尺寸，然后进行验算。如不满足要求，则修改截面尺寸或采取其他措施。

根据《建筑地基基础设计规范》，挡土墙基底面积及埋深按地基承载力确定，传至基础底面的荷载效应应按正常使用极限状态下荷载效应的标准组合。土体自重、墙体自重均按实际的重力密度计算，在地下水位以下时应扣去水的浮力，相应的抗力应采用地基承载力特征值。

计算挡土墙的土压力应采用承载能力极限状态荷载效应基本组合，但荷载效应组合设计值S中荷载分项系数均为1.0；但在计算挡土墙内力、确定配筋和验算材料强度时，上部结构传来的荷载效应组合和相应的基底反力，应按承载能力极限状态下荷载效应的基本组合，采用相应的荷载系数，即永久荷载对结构不利时分项系数取1.35，对结构有利时取1.0。

此外，在挡土墙设计中，波浪力、冰压力和冻胀力不同时计算。当墙身有泄水孔、墙后回填渗水的砂土时，墙前、后水位接近平衡。填料浸水后，受到水的减重作用，计算时应计入墙身浸水的上浮力及填料的减重作用。但应注意墙前、后水位的急剧变化，将会引起较大的动水压力作用。

挡土墙的计算通常包括：①抗倾覆验算；②抗滑移验算：③地基承载力验算；④墙身强度验算；⑤抗震计算。

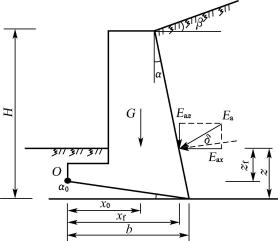
图6-29　挡土墙的稳定性验算

1) 挡土墙抗倾覆稳定性验算

研究表明，挡土墙的破坏大部分是倾覆破坏。在抗倾覆稳定验算中，将土压力Ea分解为水平分力Eax和垂直分力Eaz(图6-29)，显然，对墙趾O点的倾覆力矩为Eax·zf，而抗倾覆力矩则为G·x0+Eaz·xf。为了保证挡土墙的稳定，必须要求抗倾覆安全系数Kt(O点的抗倾覆力矩与倾覆力矩之比)≥1.6，即

(6-32)

式中:Eax——Ea的水平分力(kN/m)，Eax=Ea cos(α+δ)；

Eaz——Ea的竖向分力(kN/m)，Eaz=Ea sin(α+δ)；

G——挡土墙每延米自重(kN/m)；

xf——土压力作用点离O点水平距离(m)，xf=b-ztanα；

zf——土压力作用点离O点的高度(m)，zf=z-btanα0；

x0——挡土墙重心离墙趾的水平距离(m)；

α0——挡土墙的基底倾角(°)；

b——基底的水平投影宽度(m)；

z——土压力作用点离墙踵的高度(m)。

在软弱地基上倾覆时，墙趾可能陷入土中，使力矩中心点内移，导致抗倾覆安全系数降低，有时甚至会沿圆弧滑动而发生整体破坏，因此验算时应注意土的压缩性。

若验算结果不能满足式(6-32)要求时，可按以下措施处理：①增大挡土墙断面尺寸，使G增大，但工程量也相应增大；②加大x0，伸长墙趾。但墙趾过长时，若厚度不够，则需配置钢筋；③ 墙背做成仰斜，可减小土压力；④在挡土墙垂直墙背上做卸荷台，形状如牛腿(图6-30),则平台以上土压力不能传到平台以下，总土压力减小 故抗倾覆稳定性增大。

图6-30　有卸荷台的挡土墙

图6-31　挡土墙的抗滑移验算

2) 挡土墙抗滑动稳定性验算

在土压力作用下，挡土墙也可能沿基础底面发生滑动。在抗滑移稳定验算中，如图6-31所示的挡土墙，将主动土压力Ea及挡土墙重力G各分解为平行与垂直于基底的两个分力，滑移力为Eat，抗滑移力为Ean及Gn在基底产生的摩擦力。为防止发生滑动破坏，要求基底的抗滑安全系数Ks(抗滑力与滑动力之比)≥1.3，即:

(6-33)

式中：Ks——抗滑移安全系数；

Gn——挡土墙自重在垂直于基底平面方向的分力(kN)，Gn=Gcosα0；

Gt——挡土墙自重在平行于基底平面方向的分力(kN)，Gt=Gsinα0；

Ean——Ea在垂直于基底平面方向的分力(kN)，Ean=Easin(α+α0+δ)；

Eat——Ea在平行于基底平面方向的分力(kN)，Eat=Eacos(α+α0+δ)；

μ——土对挡土墙基底的摩擦系数，宜按试验确定，也可以按表6-5选用。

表6-5　土对挡土墙基底的摩擦系数μ

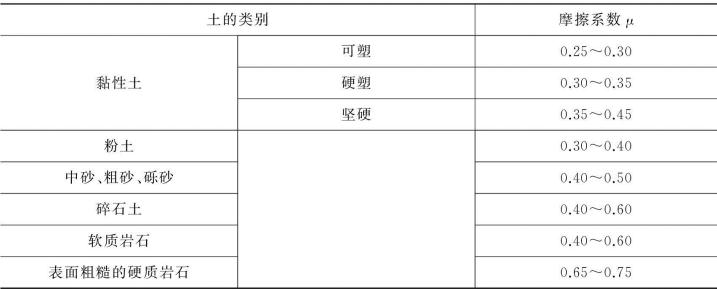
注：① 对易风化的软质岩石和Ip>22的黏性土，μ值应通过试验测定。

② 对碎石土，可根据其密实度、填充物状况、风化程度等确定。

若墙背为垂直时，则α=90°；基底水平时，α0=0。那么

Gn=G，　Gt=0

Ean=Ea·sinδ

(6-34)

Eat=Ea·cosδ

(6-35)

若验算不能满足式(6-33)要求，可采取以下措施加以解决：①修改挡土墙断面尺寸，以加大G值；②墙基底面做成砂、石垫层，以提高μ值；③墙底做成逆坡(如图6-26)，利用滑动面上部分反力来抗滑；④在软土地基上，其他方法无效或不经济时，可在墙踵后加托板，利用托板上的土重来抗滑,托板与挡土墙之间应用钢筋连接。

3) 挡土墙地基承载力验算

挡土墙地基承载力验算与一般偏心受压基础验算方法相同，先求出作用在基底上的合力及其合力的作用点位置。挡土墙重力G与土压力Ea的合力E可用平行四边形法则求得。如图6-32所示，将合力E的作用线延长与基底相交于点m，在m点处将合力E再分解为两个分力En及Et，其中En为垂直于基底的分力(即为作用在基底上的垂直合力N)，对基底形心的偏心距为e，可根据偏心受压计算公式计算基底压力并进行验算(图6-33)。

(6-36)

(6-37)

垂直于基底的分力为：

En=E·cos(α-α0-θ-δ)

(6-38)

Et=E·sin(α-α0-θ-δ)

(6-39)

如图6-33所示，可按下述方法求出基底合力N的偏心距e：先将主动土压力分解为垂直分力Eaz与水平分力Eax，然后将各力G、Eaz、Eax及N对墙踵O点取矩，根据合力矩等于各分力矩之和的原理，便可求得合力N作用点对O点的距离c及对基底形心的偏心距e。

N·c=Gx0+Eaz·xf-Eax·zf

(6-40)

(6-41)

(6-42)

式中:b′——基底斜向宽度。

验算挡土墙的地基承载力按下式进行：

当偏心距时，基底压力呈梯形或三角形分布(如图6-33)。

图6-32　地基承载力验算(一)

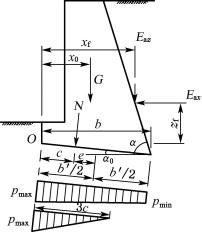
图6-33　地基承载力验算(二)

(6-43)

当偏心距时，则基底压力呈三角形分布(如图6-33)。

(6-44)

式中:fa——修正后的地基承载力特征值，当基底倾斜时，应乘以0.8的折减系数。

若挡土墙墙背垂直、基底水平时，则α=90°，α0=0，b′=b，将它们代入上述各式计算，此时N垂直基底水平宽度b、c及e均为水平距离。

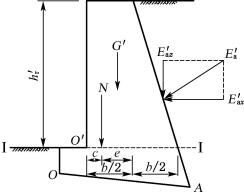
图6-34　墙身强度验算

当基底压力超过地基土的承载力特征值时，可增大底面宽度。

4) 挡土墙墙身强度验算

重力式挡土墙一般用毛石砌筑，需验算任意墙身截面处的法向应力和剪切应力，这些应力应小于墙身材料极限承载力。对于截面转折或急剧变化的地方，应分别进行验算。就是说，墙身强度验算取墙身薄弱截面进行，如图6-34所示取截面 Ⅰ - Ⅰ，首先计算墙高为时的土压力及墙身重G′，用前面的方法求出合力N及其作用点，然后按砌体受压公式进行验算。

(1) 抗压验算

N≤γa·ψ·A·f

(6-45)

式中:N——由设计荷载产生的纵向力；

γa——结构构件的设计抗力调整系数，取γa=1.0；

ψ——纵向力影响系数，根据砂浆强度等级β、e/h查表求得；

β——高厚比β=H0/h，在求纵向力影响系数时先对β值乘以砌体系数，对粗料石和毛石砌体为1.5，H0为计算墙高取为墙高)，h为墙的平均厚度；

e——纵向力的计算偏心距e=ek+ea，ek为标准荷载产生的偏心距，ea为附加的偏心距，；

A——计算截面面积，取1m长度；

f——砌体抗压设计强度。

(2) 抗剪验算

Q≤γa(fv+0.18σu)·A

(6-46)

式中:Q——由设计荷载产生的水平荷载；

fv——砌体设计抗剪强度；

σu——恒载标准值产生的平均压应力。

5) 挡土墙的抗震计算

计算地震区挡土墙时需考虑两种情况，即有地震时的挡土墙和无地震时的挡土墙。在这两种情况的计算结果中，选用其中墙截面较大者。这是因为在考虑地震附加组合时，安全度降低。有时算出的墙截面可能反而比无地震时的小，此时，应选用无地震时的墙截面。

(1) 抗倾覆验算(如图6-35)

(6-47)

(2) 抗滑移验算(如图6-36)

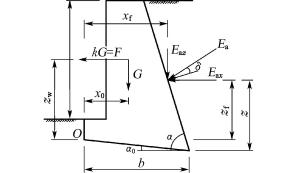
图6-35　抗倾覆验算(有地震力)

图6-36　抗滑移验算(有地震力)

(6-48)

式中:F——地震力，F=k·G。

(3) 地基承载力验算(如图6-37)

当基底合力的偏心距时：

(6-49)

当地基合力的偏心距时：

(6-50)

式中

(6-51)

(4) 墙身强度验算(如图6-38)

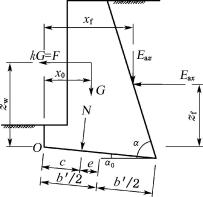
图6-37　地基承载力验算(有地震力)

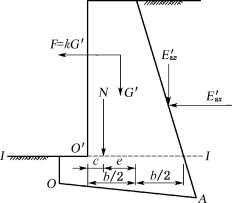
图6-38　墙身强度验算(有地震力)

① 抗压验算

N≤γa·ψ·A·f

(6-52)

② 抗剪验算

Q≤γa(fv+0.18σu)·A

(6-53)

计算Q值时，要考虑地震力F。

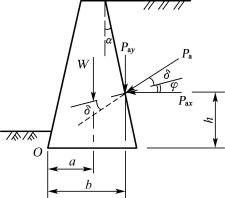
图6-39　例6-4图示

【例6-4】　已知某挡土墙墙高H=6.0m，墙背倾斜ε=10°，填土表面倾斜β=10°，墙摩擦角δ=20°，墙后填土为中砂，内摩擦角φ=30°，重度γ=18.5kN/m3，如图6-39所示，地基承载力设计值f=180kPa。设计挡土墙的尺寸。

【解】　(1) 初定挡土墙截面尺寸

设计挡土墙顶宽1.0m，底宽5.0m。墙自重为:

=3×6×24=432kN/m

(2) 土压力计算

根据题意应用库仑压力理论，计算作用于墙上的主动土压力。主动土压力系数Ka，据已知φ=30°，δ=20°，ε=10°，β=10°，查表得Ka=0.46。由公式(6-23)得：

×18.5×62×0.46=153kN/m

土压力的竖向分力为：

Pay=Pasin(δ+ε)=Pasin30°=153×0.5=76.5kN/m

土压力的水平分力为：

Pax=Pa·cos(δ+ε)=Pa·cos30°=153×0.866=132.5kN/m

(3) 抗滑稳定验算

墙底对地基中砂的摩擦系数μ，查表(6-5)得μ=0.4。应用公式(6-33)得抗滑稳定安全系数：

，安全

因安全系数偏大，为节省工程量修改挡土墙尺寸，将墙底宽5.0m减小为4.0m，则挡土墙自重为：

修改尺寸后抗滑稳定安全系数：

(4) 抗倾覆验算

求出作用在挡土墙上诸力对墙踵O点的力臂。自重W′的力臂a=2.17m；Pay的力臂b=3.65m；Pax的力臂h=2.00m。

应用公式(6-32)可得抗倾覆稳定安全系数为：

，安全。

(5) 地基承载力验算

① 作用在基础底面上总的竖向力

N=W′+Pay=360+76.5=436.5kN/m

② 合力作用点与墙趾O点距离

③ 偏心距

④ 基底边缘应力

⑤ 要求满足下列公式

(138.6+79.6)=109.1kPa<fa=180kPa

pmax=138.6kPa<1.2fa=1.2×180=216kPa

基底平均应力与最大应力均满足要求。

最终确定挡土墙截面尺寸：顶宽为1.0m，底宽为4.0m。

6.7　悬臂式挡土墙

悬臂式挡土墙一般用钢筋混凝土建造，它由三个悬臂板组成，即立壁、墙趾悬臂和墙踵悬臂。如图6-40所示，墙的稳定主要靠墙踵底板上的土重，而墙体内的拉应力则由钢筋承担。因此，这类挡土墙的优点是能充分利用钢筋混凝土的受力特性，墙体截面较小，适用于墙高超过6m，地基土质较差，缺乏当地材料以及工程比较重要时采用。在市政工程以及厂矿贮库中广泛应用这种挡土墙。

6.7.1　悬臂式挡土墙的构造特点

悬臂式挡土墙是将挡土墙设计成悬臂梁形式(图6-40)，b/H1=1/2～2/3，墙趾宽度b1约等于1/3b。墙身(立壁)承受着作用在墙背上的土压力所引起的弯曲应力。为了节约混凝土材料，墙身常做成上小下大的变截面(图6-40(a))。有时在墙身与底板连接处设置支托(图6-40(b))，也有将底板反过来设置(图6-40(c))，但比较少见。

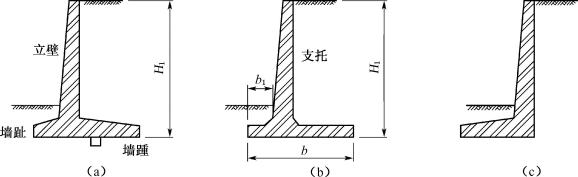
图6-40　悬臂式挡土墙

墙趾和墙踵均承受着弯矩，可按悬臂板进行设计。墙趾和墙踵宜做成上斜下平的变截面，这样不但节约混凝土，而且有利于排水。基础底板的厚度宜与墙身下端相等。

当采用双排钢筋时，墙身顶面最小宽度宜为200mm；如果墙高较小，墙身较薄，墙内配筋采用单排钢筋，则墙身顶面最小宽度可适当减小。墙身面坡采用1∶0.02～0.05，底板最小宽度为200mm，若挡土墙高超过6m，宜加扶壁柱。

挡土墙后应做好排水措施，以消除水压影响，减少墙背的水平推力。通常在墙身中每隔2～3m设置一个100～150mm孔径的泄水孔。墙后做滤水层，墙后地面宜铺筑黏土隔水层，墙后填土时，应采用分层夯填方法。在严寒气候条件下有冻胀可能时，最好以炉渣填充。

一般每隔20～25m设一道伸缩缝，当墙面较长时，可采用分段施工以减少收缩影响。

若挡土墙的抗滑移不满足要求时，可在基础底板加设防滑键。防滑键设在墙身底部，如图6-40(a)所示，键的宽度应根据剪力要求，其最小值为30cm。

钢筋布置的构造要求按设计规范的规定处理。墙身受拉一侧按计算配筋，在受压一侧为了防止产生收缩与温度裂缝也要配置纵横向的构造钢筋网φ10@300，其配筋率不低于0.2%。计算截面有效高度h0时，钢筋保护层应取30mm；对于底板，不小于50mm，无垫层时不小于70mm。

6.7.2　悬臂式挡土墙的设计计算

悬臂式挡土墙设计，分为墙身截面尺寸拟定及钢筋混凝土结构设计两部分。

确定墙身的截面尺寸，是通过试算法进行的。其做法是先拟定截面的尺寸，计算作用于其上的土压力，通过稳定验算来确定墙踵板和墙趾板的长度。

钢筋混凝土结构设计，则是对已确定的墙身截面尺寸进行内力计算和设计钢筋。

悬臂式挡土墙，一般也以墙长方向取一延米进行计算。

1) 墙身截面尺寸的拟定

根据构造要求，初步拟定出试算的墙身截面尺寸：墙高根据工程需要确定，墙顶宽可选用15～25cm。墙背取竖直面，墙面取1∶0.02～1∶0.05斜度的倾斜面，从而定出立板的截面尺寸。底板在与立板相接处厚度为(1/12～1/10)H，而墙趾板与墙踵板端部厚度不小于20～30cm，其密度B可近似取(0.6～0.8)H，当地下水位高或软弱地基时，B值应增大。墙踵板及墙趾板的具体长度将由全墙的稳定条件试算确定。

(1) 墙踵板的长度

墙踵板长可按下式确定：

(6-54)

式中：Ks——滑动稳定安全系数；

μ——基底摩擦系数；

∑G——墙身自重(kN/m)；

Eax——主动土压力水平分力(kN/m)。

(2) 墙趾板长度

墙趾板的长度，根据全墙抗倾覆稳定系数公式、基底合力偏心距e限制和基底地基承载力等要求来确定。

2) 结构设计

(1) 确定侧压力

① 无地下水(或排水良好)时(图6-41(a))

主动土压力Ea=Ea1+Ea2。当墙背直立、光滑、填土面水平时：

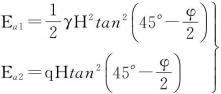
(6-55)

式中：Ea1——由墙后土体产生的土压力(N/m，kN/m)；

Ea2——由填土面上均布荷载q产生的土压力(N/m，kN/m)。

② 有地下水时(图6-41(b))

在地下水位处：

(6-56)

地下水位以下：

(6-57)

(2)内力及配筋计算

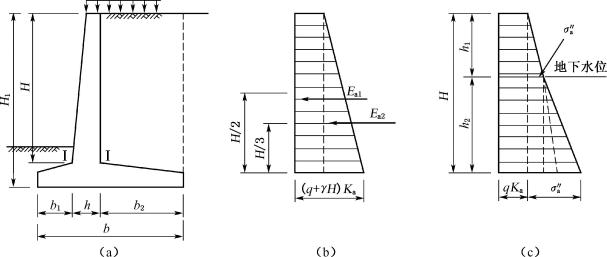
图6-41　侧压力计算

① 墙身内力及配筋计算

挡土墙的墙身按下端嵌固在基础板中的悬臂板进行计算，每延米的设计弯矩值如下(图6-41(a))：

(6-58)

式中:γ0——结构重要性系数，对于重要的构筑物取γ0=1.1，对于一般的构筑物取γ0=1.0，对于次要的取γ0=0.9；

γC——墙后填土的荷载分项系数，可取γC=1.2；

γQ——墙面均布活载的荷载分项系数，取γQ=1.4。

根据式(6-58)算出的弯矩M为墙身底部的嵌固弯矩。由于沿墙身高度方向的弯矩从底部(嵌固弯矩)向上逐渐变小，其顶部弯矩为零，故墙身厚度和配筋可以沿墙高由下到上逐渐减少。墙身面坡可采用1∶0.02～1∶0.05，墙身顶部最小宽度为200mm。配筋方法：一般可将底部钢筋的1/2至1/3伸至顶部，其余的钢筋可交替在墙高中部的一处或两处切断。受力钢筋应垂直配置于墙背受拉边，而水平分布钢筋则应与受力钢筋绑扎在一起形成一个钢筋网片，分布钢筋可采用φ10@300。若墙身较厚，可在墙外侧面(受压的一侧)配置构造钢筋网片φ10@300 (纵横两个方向)，其配筋率不少于0.2%。受力钢筋的数量，可按下式计算：

(6-59)

式中:As——受拉钢筋截面面积(m2)；

γs——系数(与受压区相对高度有关，可预先算出，列出表格)；

fy——受拉钢筋设计强度(kPa)；

h0——截面有效高度(m)。

② 地基承载力验算

墙身截面尺寸及配筋确定后，可假定基础底板截面尺寸，设底板宽度为b，墙趾宽度为b1，墙纵板宽度为b2(如图6-42)及底板厚度为h，并设墙身自重G1、基础板自重G2、墙踵板在宽度b2内的土重G3、墙面的活荷载G4、土的侧压力及，由下式可以求得合力的偏心距e值：

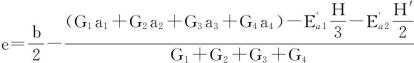
(6-60)

当e≤b/6时，截面全部受压

(6-61)

当e>b/6时，截面部分受压

(6-62)

式中:∑G——为G1、G2、G3、G4之和；

c——合力作用点至O点的距离。

所要满足的条件：

(6-63)

(6-64)

式中:fa——修正后的地基承载力特征值。

③ 墙趾板内力及配筋计算

作用在墙趾上的力有基底反力、突出墙趾部分的自重及其上土体重量，墙趾截面上的弯矩M可由下式算出(如图6-42)：

式中:Ma——墙趾板自重及其上土体重量作用下产生的弯矩(kN·m)。

由于墙趾板自重很小，其上土体重量在使用过程中有可能被移走，因而一般可忽略这两项力的作用，也即Ma=0。上式可写为：

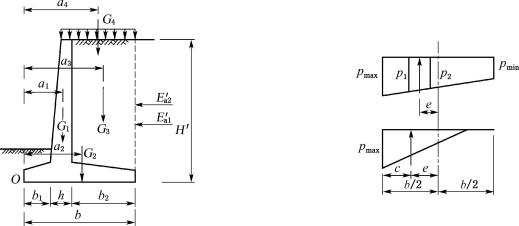
图6-42　悬臂式挡土墙受力计算示意图

(6-65)

按式(6-59)计算求得的钢筋数量应配置在墙趾的下部。

④ 墙踵板内力及配筋计算

作用在墙踵(墙身后的基础板)上的力有墙踵部分的自重(即G2的一部分，如图6-42)及其上土体重量G3、均布活荷载G4、基底反力，在这些力的共同作用下，使突出的墙踵向下弯曲，产生弯矩M2可由下式算得(如图6-42)：

(6-66)

式中:q1——墙踵自重及G3、G4产生的均布荷载。

根据弯矩M2计算求得的钢筋应配置在基础板的上部。

⑤ 稳定性验算

抗倾覆稳定验算(如图6-42)：

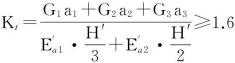
(6-67)

式中:G1、G2——墙身自重及基础板自重(kN)；

G3——墙踵上填土重(kN)。

抗滑移稳定验算(如图6-42)：

(6-68)

式(6-68)中不考虑活荷载G4，当有地下水浮力Q时，(G1+G2+G3)中要减去Q值。

(3) 提高稳定性的措施

当稳定性不够时，应采取相应措施。提高稳定性的常用措施有以下几种：

① 减少土的侧压力。墙后填土换成块石，增加内摩擦角φ值，这样可以减少侧压力。或在挡土墙立壁中部设减压平台，平台宜伸出土体滑裂面以外，以提高减压效果，常用于扶壁式挡土墙(如图6-43)。

图6-43　挡土墙立壁中部设减压平台示意图

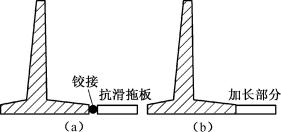
图6-44　抗滑拖板加设示意图

图6-45　倾斜面基础底板受力示意图

② 增加墙踵的悬臂长度。可以在原基础底板墙踵后面加设抗滑拖板，如图6-44(a)所示，抗滑拖板与墙踵铰接连接。也可以在原基础底板墙踵部分加长，如图6-44(b)所示。墙背后面堆土重增加，使抗倾覆和抗滑移能力得到提高。

③ 提高基础抗滑能力

A.基础底板做成倾斜面(如图6-45)。倾斜角α0≤10°。

N=∑Gcosα0+Easinα0

抗滑移力

(6-69)

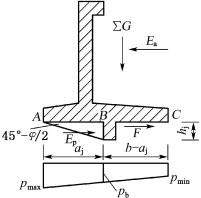
图6-46　防滑键设置示意图

滑移力

Eacosα0=∑Gsinα0

(6-70)

如图6-45所示，如果倾斜坡度为1∶6时，则cosα0=0.986，sinα0=0.164。由公式(6-69)、式(6-70)可以看出，抗滑移力增加而滑移力却减少了。

B.设置防滑键。如图6-46所示，防滑键设置于基础底板下端，键的高度hj与键离墙趾端部A点的距离aj的比例，宜满足下列条件：

(6-71)

被动土压力Ep值

(6-72)

当键的位置满足式(6-71)时，被动土压力Ep最大。键后面土与底板间的摩擦力F为：

(6-73)

应满足条件

(6-74)

式中的ψp值是考虑被动土压力Ep不能充分发挥的一个影响系数，一般可取ψp=0.5。

C.在基础底板底面夯填300～500mm厚的碎石以增加摩擦系数μ值，提高挡土墙抗滑移力。

6.8　扶壁式挡土墙

扶壁式挡土墙设计与悬臂式挡土墙设计相近，但有其自己的特点。扶壁式挡土墙设计内容主要包括墙身构造设计、墙身截面尺寸的拟定、墙身稳定性和基底应力及合力偏心距验算、墙身配筋设计和裂缝开展宽度验算等。墙底板各部分尺寸、立壁和墙底板厚度的计算，墙身稳定性和基底应力及合力偏心距验算等均与悬臂式挡土墙相同。

6.8.1　扶壁式挡土墙的构造

扶壁式挡土墙墙高不宜超过15m，一般在9～10m左右，分段长度不应大于20m。扶肋间距应根据经济性要求确定，一般为1/4～1/2墙高。每段中宜设置三个或三个以上扶肋，扶肋厚度一般为扶肋间距的1/10～1/4，但不应小于0.3m。采用随高度逐渐向后加厚的变截面，也可采用等厚式以利于施工。

图6-47　扶壁式挡土墙构造(单位：cm)

墙面板宽度和墙底板厚度与扶肋间距成正比，墙面板顶宽不得小于0.2m，可采用等厚的垂直面板。墙踵板宽一般为墙高的1/4～1/2，且不小于0.5m。墙趾板宽宜为墙高的1/20～1/5，墙底板板端厚度不小于0.3m。

扶壁式挡土墙有关构造要求如图6-47所示，其余要求同悬臂式挡土墙。

为了提高扶壁式挡土墙的抗滑能力，墙底板常设置凸榫，为使凸榫前的土体产生最大的被动土压力，墙后的主动土压力不因设凸榫而增大，故应注意凸榫设置的位置。通常将凸榫置于通过墙趾与水平面成角线和通过墙踵与水平面成角线的范围内。凸榫高则应根据凸榫前土体的被动土压力能够满足抗滑稳定性要求而定。

6.8.2　扶壁式挡土墙的设计计算

1) 墙身设计计算

(1) 计算模型和计算荷载

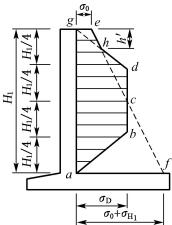
图6-48　墙面板简化土压应力图

墙面板计算通常取扶肋中至扶肋中或跨中至跨中的一段为计算单元，视为固支于扶肋及墙踵板上的三向固支板，属超静定结构，一般作简化近似计算。计算时将其沿墙高或墙长划分为若干单位宽度的水平板条与竖向板条，假定每一单元条上作用均布荷载，其大小为该条单元位置处的平均值，近似按支撑于扶肋上的连续板来计算水平板条的弯矩和剪力；按固支于墙底板上的刚架梁来计算竖向板条弯矩。

墙面板的荷载仅考虑墙后主动土压力的水平分力，而墙自重、土压力竖向分力及被动土压力等均不考虑。为简化计算，将作用于墙面板上的水平土压力图形afeg近似地用abdheg表示的土压力图形来代替，如图6-48所示，其中土压应力为：

(6-75)

式中：σD=σ0+σH1/2，σ0=γKah0，σH1=γKaH1。

(2)水平内力

根据墙面板计算模型，水平内力计算简图如图6-49所示。各内力分别为：

支点负弯矩

(6-76)

支点剪力

Q=σpil/2

(6-77)

跨中正弯矩

(6-78)

边跨自由端弯矩

M3=0

式中：l——扶肋间净距(m)。

墙面板承受的最大水平正弯矩及最大水平负弯矩在竖直方向上分别发生在扶肋跨中的H1/2处和扶肋固支处的第三个H1/4处，如图6-50所示。

设计采用的弯矩值和实际弯矩值相比是偏安全的(如图6-49(c))。例如，对于固端梁而言，当它承受均布荷载σpi时，其跨中弯矩应为σpil2/24。但是，考虑到墙面板虽然按连续板计算，然而它们的固支程度并不充分，为安全计，设计值按式(6-78)确定。

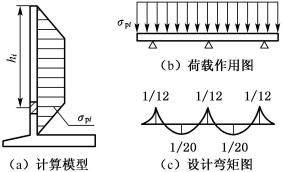
图6-49　墙面板的水平内力计算

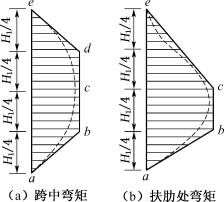
图6-50　墙面板跨中及扶肋处弯矩图

(3) 竖直弯矩

墙面板在土压力的作用下，除了产生上述水平弯矩外，将同时产生沿墙高方向的竖直弯矩。其扶肋跨中的竖直弯矩沿墙高的分布如图6-51(a)所示，负弯矩出现在墙背一侧底部H1/4范围内；正弯矩出现在墙面一侧，最大值在第三个H1/4段内。其最大值可近似按下列公式计算：

竖直负弯矩:

MD=-0.03(σ0+σH1)H1l

(6-79)

竖直正弯矩:

M=0.03(σ0+σH1)H1l/4

(6-80)

沿墙长方向(纵向)，竖直弯矩的分布如图6-51(b)所示，呈抛物线形分布。设计时，可采用中部2l/3范围内的竖直弯矩不变，两端各l/6范围内的竖直弯矩较跨中减少一半的阶梯形分布。

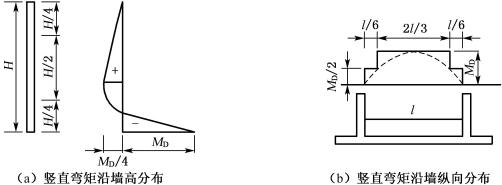
图6-51　墙面板竖直弯矩图

(4) 扶肋外悬臂长度l′的确定

扶肋外悬臂节长l′，可按悬臂梁的固端弯矩与设计采用弯矩相等求得(如图6-50)，即：

于是得:

l′=0.41l

(6-81)

2) 墙踵板设计计算

(1) 计算模型与计算荷载

墙踵板可视为支撑于扶肋上的连续板，不计墙面板对它的约束，而视其为铰支。内力计算时，可将墙踵板顺墙长方向划分为若干单位宽度的水平板条，根据作用于墙踵板上的荷载，对每一连续板条进行弯矩、剪力计算，并假定竖向荷载在每一连续板条上的最大值均匀作用在板条上。

作用在墙踵板上的力有计算墙背与实际墙背间的土重及活载W1、墙踵板自重W2、作用在墙踵板顶面上的土压力竖向分力W3(EB3y)、作用在墙踵板端部的土压力的竖向分力W4(Ety)、由墙趾板固端弯矩M1作用在墙踵板上引起的等代荷载W5、地基反力等，如图6-52(a)所示。

为简化计算，假设W3为中心荷载，如图6-52(b)所示；W4是悬臂端荷载Ety所引起的，如图6-52(c)所示，实际应力呈虚线表示的二次抛物线分布，简化为实线表示的三角形分布；M1引起的等代荷载的竖直应力近似地假设成图6-52(d)所示的抛物线形，其重心位于距固支端5/8B3处，以其对固支端的力矩与M1相平衡，可得墙踵处的应力。

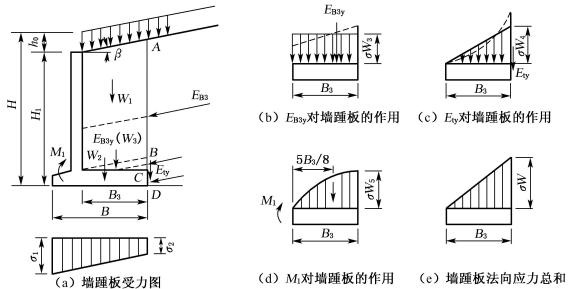
图6-52　墙踵板计算荷载图式

将上述荷载在墙踵板上引起的竖向应力叠加，即可得到墙踵板的计算荷载。由于墙面板对墙踵板的支撑约束作用，在墙踵板与墙面板衔接处，墙踵板沿墙长方向板条的弯曲变形为零，并向墙踵方向变形逐渐增大。故可近似假设墙踵板的计算荷载为三角形分布，最大值σW在踵点处(如图6-52(e))，于是得：

σW　=σW1+σW2+σW3+σW4+σW5-σ2

即

(6-82)

式中：EB3——作用在BC面上的土压力(kN)；

Et——作用在CD面上的土压力(kN)；

M1——墙趾板固端处的计算弯矩(kN·m)；

γ、γh——墙后填土和钢筋混凝土的容重(kN/m3)；

t3——墙踵板厚度(m)；

σ2——墙踵板端处的地基反力(kPa)。

(2) 纵向内力

墙踵板顺墙长方向(纵向)板条的弯矩和剪力计算与墙面板相同，各内力分别为：

支点负弯矩

(6-83)

支点剪力

Q=σWl/2

(6-84)

跨中正弯矩

(6-85)

边跨自由端弯矩

M3=0

(3) 横向弯矩

墙踵板沿板宽方向(横向)的弯矩由两部分组成：①在图6-52(e)所示的三角形分布荷载作用下产生的横向弯矩，最大值出现在墙踵板的根部。由于墙踵板的宽度通常只有墙高的1/3左右，其值一般较小，对墙踵板横向配筋不起控制作用，故不必计算此横向弯矩。②由于在荷载作用下墙面板与墙踵板有相反方向的移动趋势，即在墙踵板根部产生与墙面板竖直负弯矩相等的横向负弯矩，沿纵向分布与墙面板的竖直弯矩沿纵向分布的相同，如图6-51(b)所示。

3) 扶肋设计计算

(1) 计算模型和计算荷载

扶肋可视为锚固在墙踵板上的“T”形变截面悬臂梁，墙面板则作为该“T”形梁的翼缘板，如图6-53(a)所示。翼缘板的有效计算宽度由墙顶向下逐渐加宽，如图6-53(a)、(b)所示。为简化计算，只考虑墙背主动土压力的水平分力，而扶肋和墙面板的自重以及土压力的竖向分力忽略不计。

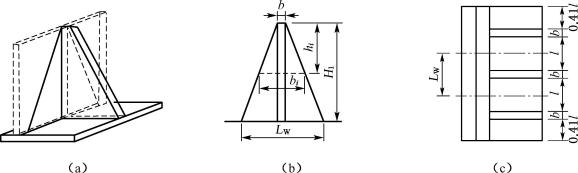
图6-53　扶肋计算图式

(2) 剪力和弯矩

悬臂梁承受两相邻扶肋的跨中至跨中长度LW与墙面板高H1范围内的土压力。在土压力EH1(图6-52(a)中，作用在AB面上的土压力)的水平分力作用下，产生的剪力和弯矩为：

Kacosβ

(6-86)

(6-87)

式中：Qhi、Mhi——高度为hi(从墙顶算起)截面处的剪力(kN)和弯矩(kN·m)；

Lw——跨中至跨中的计算长度(m)。

如图6-53(c)所示计算长度Lw，按下式计算，且LW≤b+12B2。

(6-88)

(3) 翼缘宽度

扶肋的受压区有效翼缘宽度bi，墙顶部bi=b，底部bi=LW(或12B2)，中间为直线变化，如图6-53(b)所示，即：

(6-89)

或

(6-90)

图6-54　扶壁式挡土墙配筋示意图

4) 配筋设计

扶壁式挡土墙的墙面板、墙趾板、墙踵板按矩形截面受弯构件配筋，如图6-54所示，而扶肋按变截面“T”形梁配筋。

(1)墙面板

① 水平受拉钢筋。墙面板的水平受拉钢筋分为内、外侧钢筋两种。内侧水平受拉钢筋N2布置在墙面板靠填土一侧，承受水平负弯矩，以扶肋处支点弯矩设计，全墙可分为3～4段。外侧水平受拉钢筋N3布置在中间跨墙面板临空一侧，承受水平正弯矩，该钢筋沿墙长方向通长布置。为方便施工，可在扶肋中心切断。沿墙高可分为几个区段进行配筋，但区段不宜分得过多。

② 竖向受力钢筋。墙面板的竖向受力钢筋也分内、外两侧。内侧竖向受力钢筋N4布置在靠填土一侧，承受墙面板的竖直负弯矩。该筋向下伸入墙踵板不少于一个钢筋锚固长度；向上在距墙踵板顶高H1/4加上一个钢筋锚固长度处切断。每跨中部2l/3范围内按跨中的最大竖直负弯矩MD配筋，靠近扶肋两侧各l/6部分按MD/2配筋，如图6-51所示。外侧竖向受力钢筋应布置在墙面板临空一侧，承受墙面板的竖直正弯矩。该钢筋通长布置，兼作墙面板的分布钢筋之用。

③ 墙面板与扶肋间的U形拉筋。连接墙面板与扶肋的U形拉筋N6，其开口向扶肋的背侧。该钢筋每一肢承受高度为拉筋间距水平板条的支点剪力口，在扶肋水平方向通长布置。

(2) 墙踵板

墙踵板顶面横向水平钢筋N7，是为了墙面板承受竖直负弯矩的钢筋N4得以发挥作用而设置的。该筋位于墙踵板顶面，垂直于墙面板方向。其布置与钢筋N4相同，该筋一端插入墙面板一个钢筋锚固长度；另一端伸至墙踵端，作为墙踵板纵向钢筋N8的定位钢筋。如钢筋N7的间距很小，可以将其中一半在距墙踵端B3/2减一个钢筋锚固长度处切断。

墙踵板顶面和底面纵向水平受拉筋N8、N9(图中未示)，承受墙踵板在扶肋两端的负弯矩和跨中正弯矩。该钢筋切断情况与N2、N3相同。

连接墙踵板与扶肋之间的U形钢筋N10(图中未示)，其开口向上。可在距墙踵板顶面一个钢筋锚固长度处切断，也可延至扶肋的顶面，作为扶肋两侧的分布钢筋。在垂直于墙面板方向的钢筋分布与墙踵板顶面纵向水平钢筋N8相同。

(3) 墙趾板

同悬臂式挡土墙墙趾板的配筋设计。

(4) 扶肋

扶肋背侧的受拉钢筋N11(图中未示)应根据扶肋的弯矩图选择2～3个截面，分别计算所需的拉筋根数。为节省混凝土，钢筋N11可多层排列，但不得多于3层。其间距应满足规范要求，必要时可采用束筋。各层钢筋上端应按不需此钢筋的截面再延长一个钢筋锚固长度，必要时，可将钢筋沿横向弯入墙踵板的底面。

除受力钢筋外，还需根据截面剪力配置箍筋，并按构造要求布置构造钢筋。

6.9　加筋土挡墙

6.9.1　加筋土结构及其发展概述

土体具有一定的抗剪强度和抗压强度，但抗拉强度很低。在土体中掺入或铺设适量的拉筋材料后，可以不同程度地改善土体的强度与变形特征。将拉筋材料埋置在土体中，可以扩散土体的应力、增加土体的模量、传递拉应力、限制土体侧向变形，同时还能增加土体和其他材料的摩阻力，提高土体及有关结构物的稳定性。因此，在填土中加入抗拉材料，通过摩擦力将拉筋材料的抗拉强度与土体的抗压强度结合起来，增强土体的稳定性，使土体的整体强度得以提高。该技术已广泛用于修筑路堤、挡土墙、桥台等工程。

从广义上讲，凡在土体中加入筋材，充分利用土体的抗压强度和筋材的抗拉强度的稳定结合体均可为加筋土结构。如：在软土路基的基底铺设单层或多层高强度的土工织物或土工格栅来约束浅层软土地基的侧性变形，提高路堤的抗滑稳定性；在复合地基表面，利用土工合成材料和砂、碎石等组成加筋垫层，以传递和调整基底应力分布，减少不均匀沉降；在路基边坡内加入筋材，以增强边坡的稳定、防止边坡滑坡等。

加筋土结构主要由加筋材料、面层系统和回填材料三部分组成。

(1) 加筋材料。在加筋土结构系统中采用的加筋材料，按其几何形状可分为条带加筋(包括钢带、聚合物加筋带、混凝土板条等)、网眼型宽幅加筋(包括土工格栅、土工网格或钢筋网)和非网眼型宽幅加筋(主要为土工布)三种类型。目前大部分加筋土结构采用连续的土工合成材料(土工网格、土工格栅或土工布)。尤其是土工格栅，由于其具有变形模量大、抗拉强度高、韧性好、质量轻、耐腐蚀、抗老化、与土颗粒之间的相互作用强以及能在短时间内发挥加筋作用等优点而得到广泛的应用。

(2) 面层系统。面层系统是阻止两层加筋材料之间土的表面剥落而使用的加筋土结构的一部分，一般包括预制混凝土块、现浇混凝土面板、石笼、焊接钢丝网、喷浆混凝土、土工合成材料返包式面板等。加筋土结构系统中使用的面层系统由于是加筋土结构中唯一的可视部分，对美观影响很大。另外，面层系统对结构的稳定也起一定的作用，可保护回填土，防止其滑塌和侵蚀；在某种情况下，也能提供供水通道。

(3) 回填材料。对于加筋土结构，为了保证其耐久性、良好的排水系统、施工方便以及良好的加筋土作用，一般需要采用良好的粗粒土。由于筋材和填土之间的摩擦力对加筋土结构的稳定性起着重要作用，一般要求尽量选用具有良好摩擦特性的材料。国内外研究者，一是因为黏性土的内摩擦角较小，二是它的低渗透性往往会存在超孔隙水压力，降低加筋土工程的安全度，就加筋土而言，加筋土结构可采用质量较差的回填土，但高质量的回填土有排水方便的优点，而且粒料土的装卸、填土和压实过程中也有显著的优点，可提高筑坡成功率和改善坡体线性偏差。

6.9.2　土工合成材料的发展及种类

1) 加筋土结构的发展现状

加筋土的应用具有悠久的历史。公元前3000年以前，英国人曾在沼泽地带用木排修筑道路；公元前2000到公元前1000年，巴比伦人曾利用土体加筋来修筑塔庙。1965年，法国在比利牛斯山的普拉聂尔斯修建了世界上第一座加筋土挡墙。由于加筋土技术在法国的成功应用，引起了世界各国工程界、学术界的重视，其发展速度相当快，应用范围也日益广泛。20世纪70年代是加筋土技术在世界范围传播、发展的阶段，相应的试验、研究工作也同时进行。当时，研究最为活跃的当属法国桥梁道路中心、美国加州大学、日本国铁和建设省。20世纪80年代，除了进一步探讨加筋土结构的基本现状、完善设计计算理论之外，许多国家还在拓宽填料、加筋材料的应用范围方面做了大量的工作。

我国是加筋土的故乡，自古以来，筑土墙加草筋或竹筋，用柴排处理软弱地基，用土袋或树枝压条加固堤岸等，都是应用加筋土的例子。现代加筋土技术引入我国是在20世纪70年代后期。1979年，云南省煤炭设计院在云南田坝矿区建成了我国第一座加筋土挡墙储煤仓，其挡土墙部分长度80m，高2.3～8.3m，由填土和布置在填土中的筋带及墙面板三部分组成。该挡土墙的成功建造引起了我国土木建筑行业技术人员的兴趣，因为这种结构不仅施工容易，而且具有一定的经济型。与传统的砌石挡墙相比，加筋土挡墙造价较低。从技术上看，加筋土是柔性结构，对地基承载力的要求较低，易于处理，施工也无需专用机具和特别技术，工效高，易于推广，外形平整美观。因此，很多人对这种结构进行了深入研究并迅速推广使用，各省、自治区和直辖市修建的加筋土工程已经超过千项，砌墙面积超过70万m2。在大量工程实践的基础上，随着经验的积累，创造了符合我国国情的加筋土技术。

2) 土工合成材料的种类

1977年，Giroud J R 与Perfetti J率先把透水的土工合成材料称为土工织物，不透水的称为土工膜。进入20世纪80年代，为了更好地满足岩土工程的需要，土工合成材料的应用逐渐增多，以合成聚合物为原料的其他类型的土工合成材料纷纷问世，已经超出了“织物”和“膜”的范畴，两大类分法难以包含。国际土工织物学会提出了土工织物、土工膜及其相关产品的分类体系，1983年Giroud等提出的分类方法就是其中的典型代表。目前土工合成材料分类方法的趋势是抛弃以土工织物为分类主线的思路，建立便于工程应用的分类方法。通常将土工合成材料分为四大类(如图6-55)：①土工织物，属于透水的土工合成材料，以前叫土工布，所用的原材料一般为丙纶、涤纶或其他合成纤维;②土工膜，属于相对不透水的土工合成材料，所用的原材料有沥青和合成聚合物，还要有一定的填充料和外加剂，填充料有矿粉和聚合物粉末等，为了提高其耐久性和降低造价，外加剂包括增塑剂、抗老化剂、抗菌剂、各种稳定剂等；③复合土工合成材料，是土工织物、土工膜等两种以上材料复合而成的土工合成材料，包括复合土工膜、复合土工织物、复合排水材料;④特种土工合成材料，指土工织物和土工膜以外的，近十几年来研制的新型土工合成材料，能够更好地满足岩土工程的要求。

土工合成材料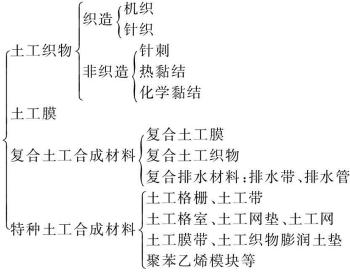

图6-55　土工合成材料的分类

土工合成材料最常用的高分子聚合物有：①聚乙烯(Polyethylene，缩写为PE)；②聚丙烯(Polypropylene，缩写为PP)；③聚酯(Polyester，缩写为PET)；④聚酰胺(Polyamide，缩写PA)；⑤聚乙烯醇(Polyvinyl Alcohol，缩写为PVA)；⑥聚氯乙烯(Polyvinyl Chloride，缩写为PVC)；⑦聚苯乙烯(Polystyrene，缩写为PS)等。

纤维分天然纤维和化学纤维。天然纤维包括棉、毛、丝、麻等；化学纤维是由各种不同原料经过化学处理和机械加工而成，包括人造纤维和合成纤维。合成纤维以聚合物为料，经过熔融或溶解成为黏稠纺丝液，在一定压力下由喷丝头喷丝，并经加工制成。合成纤维与人造纤维相比，强度较高，吸湿性较小。

商业上把人造纤维的短纤维称为纤、合成纤维的短纤维称为纶、人造纤维和合成纤维的长丝称为丝。商业产品名称统一将聚乙烯醇纤维称为维纶、聚丙烯腈纤维称为腈纶、聚乙烯纤维称为氯纶、聚丙烯纤维称为丙纶。有时在品名后加一个脂字就是指纤维上加了树脂防缩、防水等；有时为了增加弹性也添加些塑性树脂。

6.9.3　加筋土的设计计算

加筋土结构设计一般应考虑加筋土体的内部稳定性和整体稳定性。内部稳定性系指由于筋带被拉断或筋土间摩擦力不足致使加筋土结构破坏；整体稳定性系指由于加筋土外部失稳而引起的加筋土结构破坏，其包括考虑地基承载力、地基沉降、抗滑及滑坡稳定性的验算。

1) 加筋土体的内部稳定性计算

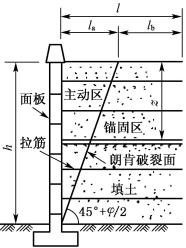
图6-56　加筋土结构示意图

主要是确定筋带的断面面积和锚固长度(或有效长度lb)，因此必须计算筋带所受到的拉力。现有计算理论较多，且不同的计算理论其结果不同，以下仅介绍常用的朗肯理论分析方法。

朗肯理论认为面板后土体呈朗肯主动状态，破裂面与水平面夹角为45°+φ/2，如图6-56所示。破裂面以左为主动区，以右为锚固区(或被动区)。当土体主动土压力充分发挥时，面板后距加筋体顶面深度z处第i根筋带所受的拉力Ti为：

Ti=Kaγzsxsy

(6-91)

式中：Ka——朗肯土压力系数，Ka=tan2(45°-φ/2)；

γ——填料的重度(kN/m3)；

z——第i层筋带距加筋体顶面的垂直距离(m)。

筋带的断面面积As(m2)可根据筋带所用的材料强度确定：

(6-92)

式中:fy——筋带材料的抗拉强度设计值(kPa)；

γG——荷载分项系数，可取γG=1.2。

计算筋带断面尺寸时，在实际工程中还应考虑防腐蚀需要增加的尺寸。此外，每根筋带在工作时还有被拔出的可能，因此尚需计算筋带抵抗被拔出的锚固长度lb。设土与筋带间摩擦系数为f，则锚固区内由于摩擦作用而使第i根筋带产生的摩擦力Tb为：

Tb=2lbbγzf

(6-93)

式中:b——筋带的宽度(m)；

f——筋带与填土之间的摩擦系数，宜通过试验确定，无试验时可取：砂土0.42～0.7，黏性土0.4～0.6，杂填土0.38～0.6。

在该深处的抗拉安全系数Kb为：

(6-94)

抗拉安全系数与深度无关，一般可取1.5～2.0。故第i根筋带的锚固长度为：

(6-95)

第i根筋带的总长度l为：

(6-96)

式中:l0——筋带的无效长度，按朗肯理论l0=htan2(45°+φ/2)。

大量工程实测资料分析表明，筋带主动区和锚固区的分界线可采用0.3h法，如图6-57所示，故筋带的无效长度l0亦可按照下式计算：

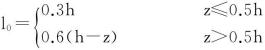
(6-97)

由此可见，计算的筋带长度随深度增加而减小。但实际工程中，为了施工方便，常采用如下规定：①当墙高小于3.0m时，可设计成为等长的筋带；②当墙高大于3.0m时，可变换筋带长度，但一般同等长度筋带变换的高度不应该小于2.0m且相邻筋带的变换长度不得小于0.5m，如图6-58(a)所示；③对于路堤式的挡土墙，如果路堤较窄，筋带可交错的排列，如图6-58(b)所示。

图6-57　0.3h法示意图

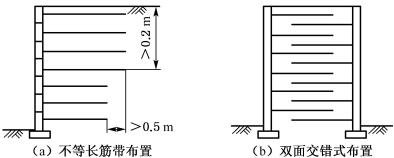
图6-58　筋带布置示意图

2) 加筋土的整体稳定性

加筋土体对地基要求不高，只要求地基可以承受加筋土重力即可，即要求作用在地基上的压应力设计值等于或小于地基承载力的设计值。此外，加筋土结构本身具有一定柔性，故对地基变形适应性远比其他挡土的结构好。

加筋土整体稳定性包括滑动、倾覆和滑动验算。只要筋带具有足够锚固长度和横断面积，就可保证面板不会出现倾覆从而丧失稳定。当验算加筋土结构底部抗滑稳定时，可将其视为墙背作用有主动土压力的整体结构，如图6-59(a)所示，抗滑安全系数取1.5。当地基很软弱时，也可能产生近似于圆弧状的滑动面，如图6-59(b)所示。当滑动破坏面垂直于加筋层面时，筋带尾端越远(①)，则加筋土所发挥的阻抗力就越大，而图中②和③所表示的滑动破坏面，筋带的抗拉强度基本没有发挥。

图6-59　加筋土稳定性验算

思考题与习题

1.什么是静止土压力、主动土压力和被动土压力？它们与挡土建筑物的位移有何关系？举工程实例说明。

2.说明“土的极限平衡状态”是什么意思，从而区分主动和被动土压力。挡土墙应如何移动，才能产生主动土压力？

3.朗肯土压力理论的基本假定是什么？对土压力的计算结果有何影响？

4.图6-60中(a)、(b)、(c)三种情况，哪种情况能直接应用朗肯土压力理论计算？哪种情况不能？为什么？

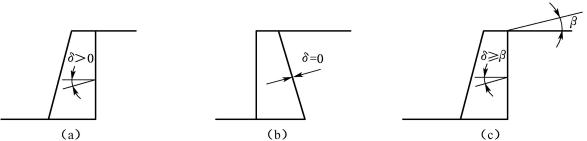
图6-60　习题4图

5.库仑土压力理论的基本假定是什么？对土压力的计算结果有何影响？

6.主动土压力是土压力中的最小值，为什么在库仑公式推导中却要找最大的Ea值作为主动土压力？

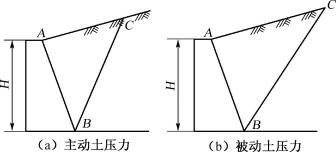
图6-61　习题7图

7.图6-61(a)、(b)中AB、BC为挡土墙受到主动、被动土压力作用时的滑动面，根据库仑土压力理论绘出：(1)沿BC、AB滑动面作用在楔体上的剪应力方向；(2)作用在AB、BC面上的反力方向。

8.试比较朗肯土压力理论和库仑土压力理论的优缺点和各自的适用范围。

9.填土表面有连续均布荷载，土压力沿深度的分布是三角形、梯形、矩形，在地下水位以下，这部分土压力是否有变化(假定水位以下φ值不变)？

10.墙后填土有地下水时，为什么不能按饱和容重计算土压力？地下水位的升降对挡土墙的稳定有何影响？

11.挡土墙通常都设有排水孔，起什么作用？如何防止排水孔失效？

12.下列几种情况下，土压力发生哪些变化？试定性绘出其变化并说明理由：(1)有地下水；(2)两层填土：γ1<γ2或γ1>γ2，(φ1=φ2时)；(3)两层填土：γ1=γ2时，φ1<φ2或φ1>φ2。

13.挡土建筑物有哪些类型和形式？它们与土压力的大小有何关系？各有何特点？

14.采用哪些措施可以提高挡土墙的稳定性？

15.为减小挡土墙的土压力，墙后填土愈松愈好对吗？为什么？从有利于墙的稳定出发，选什么填料好？

16.阐述加筋土挡墙的特点。

17.阐述通过加筋对土体改良的基本原理。

18.阐述加筋土挡墙破坏形式。

19.阐述加筋土的受力特点。

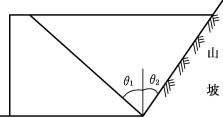
图6-62　习题20图

20.山坡挡土墙如图6-62所示，若θ1>45°-φ/2，θ2<45°-φ/2，墙面光滑，δ1=0。山坡面很粗糙，山坡与土之间的摩擦角δ2>φ，试用图解法绘出挡土墙的土压力示意图。

21.挡土墙的墙背垂直且光滑，墙后填土面水平，试定性绘出下列情况的主动土压力分布：(1)填土为均质砂土或均质黏土；(2)填土为黏土，地下水位在H/2处；(3)填土上半层为砂，下半层黏土；(4)填土为均质黏土，填土面有均布连续荷载。

22.挡土墙高5m，墙背垂直、光滑，墙后填土面水平，填土的重度γ=19kN/m3，c=10kPa，φ=30°。试确定：(1)主动土压力沿墙高的分布；(2)总主动土压力的大小和作用点位置。

23.某挡土墙高4m，墙背倾斜角α=20°，填土面倾角β=10°，填土的重度γ=20kN/m3，c=0kPa，φ=30°，填土与墙背的摩擦角δ=15°，如图6-63所示。试用库仑土压力理论计算：(1)主动土压力的大小、作用点位置和方向；(2)主动土压力沿墙高的分布。

24.一挡土墙高6m，墙背垂直、光滑，填土面水平，填土分两层，第一层为砂土，第二层为黏性土，各土层的物理力学性指标如图6-64所示，试求主动土压力强度，并绘出主动土压力沿墙高的分布。

25.挡土墙高6m，墙背垂直、光滑，墙后填土面水平，填土的重度γ=18kN/m3，c=0，φ=30°。试求：(1)墙后无地下水时的总主动土压力；(2)当地下水位离墙底2m时，作用在挡土墙上的总压力(包括土压力和水压力)，地下水位以下填土的饱和重度γsat=19kN/m3。

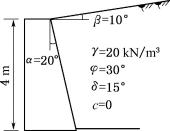
图6-63　习题23图

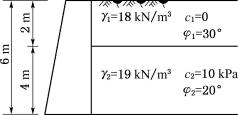
图6-64　习题24图

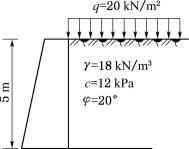
图6-65　习题26图

26.某挡土墙高5m，墙背垂直、光滑，墙后填土面水平，作用有连续均布荷载q=20kPa，填土的物理力学性指标如图6-65所示，试计算主动土压力。

图6-66　习题27图

27.如图6-66所示挡土墙，墙身砌体重度γk=22kN/m3，试验算挡土墙的稳定性。

28.某厂区拟建一挡土墙，采用加筋土挡墙形式，墙高14m,按路肩式挡土墙设计。厂区原地面为黏性土，承载力为200kPa,厚度为1.5m,其下为基岩。挡土墙设计参数如下：填料采用粉煤灰，重度为14.5kN/m3，内摩擦角为39.5°。单根筋带的断面为18mm，厚度为1.2mm，容许拉应力为30MPa。筋带与填料的摩擦系数为0.3，挡土墙与地基的摩擦系数为0.3。试完成挡土墙的设计。