作用于曲面的液体压力

作用于曲面任意点的流体静压强都沿其作用面的内法线方向垂直于作用面,但曲面各处的内法线方向不同,彼此互不平行,也不一定交于一点。因此,求曲面上的水压力时,一般将其分为水平方向和铅直方向的分力分别进行计算。本节主要研究工程中常见的柱体曲面,然后将结论推广到空间曲面。

图2 -9所示为垂直于纸面的柱体,其长度为l,受压曲面在纸上的投影为AB,其左侧承受水静压力。

图2-9　作用于柱体曲面的压力

设在曲面AB上,水深h处取一微小面积d A,作用在d A上的水静压力为

d P=p d A=γh d A

该力垂直于面积d A,并与水平面成夹角θ,此力可分解为水平和铅直两个分力。水平分力为

d P x=d P cosθ=γh d A cosθ

铅直分力为

d P z=d P sinθ=γh d A sinθ

因为d A cosθ和d A sinθ分别等于微小面积d A在铅直面上和水平面上的投影,令d A z= d A cosθ,d A x=d A sinθ,所以

d P x=γh d A z

d Pz=γh d A x

上式分别积分得

式(2 -11)右边的积分等于曲面AB在铅直平面上的投影面积A z对水面的水平轴y的静矩(截面对某个轴的静矩等于截面内各微面积乘以微面积至该轴的距离在整个截面上的积分)。设h C为A z的形心在水面下的淹没深度,则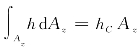。因此

P x=γh C A z

(213)

可见,作用于曲面上的水静压力P的水平分力P x等于该曲面的铅直投影面上的水静压力。因此,可以引用平面水静压力的方法求解曲面上水静压力的水平分力。

式(2-12)右边的h d A x,是以d A x为底面积,水深h为高的柱体体积。所以,∫Axh d A x即为受压曲面A B与其在自由面上的投影面积CD这两个面之间的柱体ABCD的体积,称为压力体,以V表示。压力体一般是三种面所封闭的体积:即底面是受压曲面,顶面是受压曲面边界线封闭的面积在自由面或者其延长面上的投影面,中间是通过受压曲面边界线所作的铅直投射面。所以

这就是说,作用于曲面上的水静压力P的铅直分力P z等于其压力体内的水重。

P z的方向取决于受压曲面和液体的相对位置和曲面所受相对压强的正负,可根据具体情况容易地加以判断。但是,不论P z的方向如何,它的大小都等于压力体内的液体重量,其作用线均通过压力体形心。

在求出P x和P z后,可进一步求出合力P,即

合力P的作用线与水平线的夹角θ为

例2-3　图2-10所示一水箱,左端为一半球形端盖,右端为一平板端盖。水箱上部有一加水管,已知h=600 mm,R=150 mm。试求两端盖所受的总压力及其方向。

解　(1)右端盖是一个铅垂的圆平面,只有x方向作用力,其面积为

A r=πR 2

图2-10　例2-3附图

其上作用的总压力为

F Pr=ρg(h+R)A r=520(N)

方向垂直于端盖,水平向右。

(2)左端盖

此为一半球面。由曲面上总压力的求法,将F P分解成三个方向分量F Px,F Py,F Pz。F Px=ρg(h+R)A x =ρg(h+R)πR 2 =520(N)

方向水平向左。

由于半球面关于y轴对称,故有

F Py=0

z方向总压力由压力体来求。将半球面分成A B、BE两部分,A B部分的压力体为A BCD EA,记为V ABCDEA,它为实压力体,方向向下;BE部分压力体为BCDEB,记为V BCDEB,为虚压力体,方向向上。因此总压力体为它们的代数和

V=V ABCDEA-V BCDEB=V ABEA

这正好为半球的体积。所以

因此

方向垂直向下。

所以,总作用力为

合力方向与水平方向夹角