黏性流体圆管中的层流运动

工程实际中,虽然大部分流体的流动为湍流流动,但层流流动也广泛地存在于小管径、小流量、大黏度的流动场合,如机械润滑系统、地下水渗流问题和微反应系统等。黏性流体在圆管中的层流流动是最具代表性的层流流动。

在图45所示的均匀流动中,选择半径为r,长度为l的微小圆柱,在任选的两个断面11和22列能量方程

图4-5　圆管均匀流动

由均匀流动的性质有,代入上式,得

两断面间的距离为l,过流断面面积A 1=A 2=π·r 2,在流向上,该流段所受的作用力有端面压力和外表面的黏性力。在均匀流中,流体质点作等速运动,因此流向上各力的合力为0,得

p 1 A-p 2 A-τ·l·2πr=0

整理得

则

对于圆管中的层流运动,轴对称的流动各流层间的切应力大小满足牛顿内摩擦定律式,即

由于速度u随r的增大而减小,所以等式右边加负号,以保证τ为正。

假设在均匀流中,值不随r而变。积分上式,并代入边界条件:r=r时,u=0,得 0

可见,圆管中的层流运动的断面流速分布是以管中心线为轴的旋转抛物面,见图4-6。

图4-6　圆管中层流的流速分布

当r=0时,即在管轴上,达最大流速

将式(4-15)代入平均流速定义式

比较式(4-16)和式(4-17),得

即对于圆管中的层流流动,平均流速等于最大流速的一半。

根据式(4-17),得

式中,h f/l为水力坡度,此式从理论上证明了层流单位长度上的沿程损失为常数。

将式(4-19)写成式(4-1)所示的沿程损失的一般形式,即由此式可得圆管层流的沿程阻力系数的计算式它表明圆管层流的沿程阻力系数仅与雷诺数有关,且成反比,而和管壁粗糙度无关。

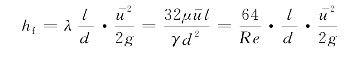
由于从理论上导出了层流时流速分布的解析式,可导出圆管层流运动的动能修正系数α和动量修正系数α0

层流时,速度分布相对不均匀,两个系数值较大,不能近似为1,在实际工程中,大部分管流为湍流,湍流掺混使断面流速分布比较均匀,因此系数α和α0均近似取为1。