突然扩大时产生阻力损失的原因在于边界层脱体。流道突然扩大,下游压强上升,流体在逆压强梯度下流动,极易发生边界层分离而产生旋涡,如图4-11(a)所示。

图4-11 突然扩大和突然缩小
流道突然缩小时,见图4-11(b),流体在顺压强梯度下流动,不致发生边界层脱体现象。因此,在收缩部分不发生明显的阻力损失。但流体有惯性,流道将继续收缩至AA面,然后流道再次扩大。这时,流体转而在逆压强梯度下流动,也就产生边界层分离和旋涡。可见,突然缩小造成的阻力主要还在于突然扩大。
有少数形状简单的局部阻碍,可以借助于基本方程求得它的阻力系数,突然扩大就是其中的一个。图4-12为圆管突然扩大处的流动。取流股将扩未扩的Ⅰ-Ⅰ断面和扩大后流速分布与湍流脉动已接近均匀流正常状态的Ⅱ-Ⅱ断面列能量方程,如果两断面间的沿程水头损失不计,则

图4-12 突然扩大

为了确定压强与流速的关系,再对Ⅰ,Ⅱ两断面与管壁所包围的流动空间写出沿流动方向的动量方程
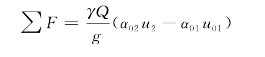
式中,∑F为作用在所取流体的全部轴向外力之和,其中包括:
(1)作用在Ⅰ断面上的总压力P 1。应指出,Ⅰ断面的受压面积不是A 1,而是A 2。其中的环形部分位于旋涡区。观察表明,这个环形面积上的压强基本符合静压强分布规律,故
P 1=p 1 A 2
(2)作用在Ⅱ断面上的总压力,P 2=p 2A 2
(3)重力在管轴上的投影

(4)边壁上的摩擦阻力忽略不计。因此,

将Q=u 2 A 2代入,化简后得

将上式带入能量方程式得
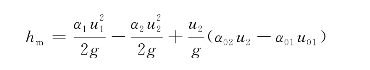
对于湍流,可取α01=α02=1,α1=α2=1。
由此可得

上式表明,突然扩大的水头损失等于以平均流速差计算的流速水头。
要把式(4-35)变换成计算局部阻力损失的一般形式只需将 代入。
代入。

所以突然扩大的阻力系数为

突然扩大前后有两个不同的平均流速,因而有两个相应的阻力系数。计算时必须注意使选用的阻力系数与流速水头相适应。
工程中使用的管件种类繁多,常见的管件、阀件及其阻力系数ζ可参考附录Ⅴ,其他的管件、阀件等的阻力系数ζ可参阅有关资料。
例4-2 所谓虹吸管即管道中一部分高出上游供水液面的管路,如图4-13所示。图中具体数值如下: H=2 m,l 1=15 m,l 2=20 m,d=200 mm,进口阻力系数ζe=1,转弯阻力系数ζb=0.2,出口阻力系数ζ0=1,λ=0.025,管中水流的最大允许真空高度[h v]=7 m。求通过虹吸管流量及管顶最大允许安装高度h max。
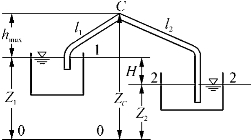
图4-13 虹吸管示意图
解 现以水平线0-0为基准线,列出图4-13中1-1、2-2能量方程。

式中 h f1,h f2——水在管长为l 1和l 2内的沿程阻力损失;
h me,h mb,h m0——分别为进口、转弯和出口处的局部阻力损失;
u——虹吸管内流速。
将式(2)和式(3)代入式(1)得

则

为了计算最大真空高度,取1-1及最高断面C-C列能量方程当
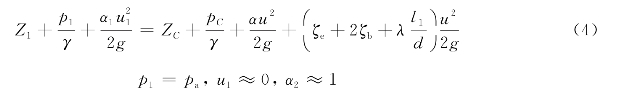
=[h v]时,ZC-Z 1=h max,则
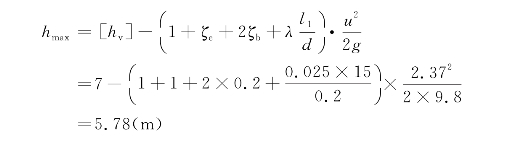
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















