泵与风机的理论特性曲线

叶轮流道的几何形状如图73所示。其中D 0为叶轮进口直径,D 1、D 2为叶片的进出口直径,b 1、b2为叶片的进出口宽度。

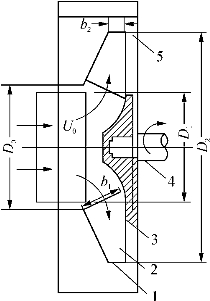
图7-3　叶轮流道的几何形状

1—叶轮前盘;2—叶片;3—叶轮后盘; 4—轴;5—机壳

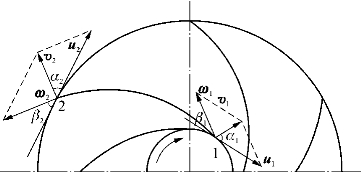
图7-4　叶片进、出口处的流体运动情况

1—进口;2—出口; u 1,u 2—叶片进出口的圆周速度;ω1,ω2—叶片进出口的相对速度;v 1,v 2—叶片进出口的绝对速度;β1,β2—叶片的进出口安装角;α1,α2—叶片的进出口工作角

流体在叶轮的运动可分解为随叶轮旋转所做的圆周牵连运动和沿叶片切向的相对运动,牵连运动和相对运动合成了流体在叶轮中的绝对运动。图7-4所示为叶片进口、出口处流体的运动情况。

绝对运动的速度向量v等于牵连运动的速度向量u与相对运动的速度向量w的矢量和,即

v=u+w　　　　　(7-3)

为便于分析,常将绝对速度v分解为与流量有关的径向分速度v r和与压头有关的切向分速度v u。流体质点的速度三角形如图7-5所示。速度三角形清楚地表达了流体在叶轮流道中的流动情况,是研究泵或风机性能的重要手段。泵与风机的性能主要取决于叶轮进口及出口处流体的运动情况。

当叶轮流道的几何形状和尺寸确定后,安装角β(叶片进出口处的切线与圆周速度反方向线之间的夹角,表明叶片的弯曲方向)、叶片直径D或半径R、叶片宽度b就确定了。如果已知叶轮转速n和流经叶轮的流量Q T,则可求得叶轮内任何半径R上某点的速度三角形。

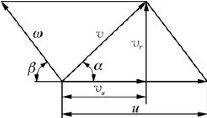
图7-5　流体质点在叶轮中运动的速度三角形

该点的圆周速度u为由于流经叶轮的流量Q T等于该点径向分速度v r乘以垂直于v r的过流断面面积F,即式中,ε为叶片排挤系数,它反映了叶片厚度对流道过流面积的遮挡程度。求得u、v r后,又已知β,则该点速度三角形不难绘出。

若流体沿径向流入叶片,通过理论计算,理论扬程H T可表示为

其中

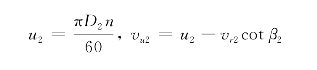
对于大小一定的泵与风机,转速不变时,用Q T表示理论流量,通过理论计算,理论扬程可表示为

HT=A-BQT　　　　(7-7)

式中,A,B为常数,分别为

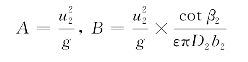
式(7-7)说明在固定转速下,不论叶型如何,泵或风机的理论扬程与理论流量成线性关系,图7-6绘出了三种不同叶型泵或风机理论上的H TQ T曲线。在无流动损失条件下,理论上的有效功率就等于轴功率,即

N T=N eT=ρg Q T H T

将式(7-7)代入,得

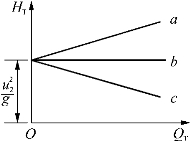
图7-6　三种叶型的H3(Q TQ3(Q T曲线

a—前向式;b—径向式;c—后向式

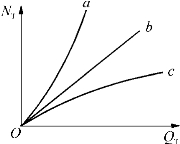
图7-7　三种叶型的N3(Q TQ 3(Q T曲线

a—前向式;b—径向式;c—后向式

可见对于不同的β2值具有不同形状的曲线,如图77所示。但当Q T=0时,三种叶型的理论轴功率都等于零,三条曲线同交于原点。

因为理想条件下(无能量损失),理论上的有效功率就等于轴功率,所以ηT=f 3(Q T)= 1,为一条直线。

根据以上分析,可以定性地说明不同叶型的理论特性曲线变化趋势。这对于后面研究泵或风机的实际特性曲线是很有意义的。同时从三种叶型的N TQ T曲线可以看出,前向叶型风机所需的轴功率随流量的增加而迅速增大,因此这种风机在运行中增加流量时,电动机超载的可能性要比径向叶型风机大得多,而后向叶型的风机几乎不会发生原动机超载的现象。