相似准则及其分析方法

流体力学实验研究的目的,就是找出流动的具体规律,即建立物理参数之间的具体关系式,也称实验关联式。在不引入相似数的情况下,要得出实验关联式就必须将具体问题所涉及的每一个物理量作为实验变量,一一进行实验测试。这样做,不仅实验工作量大,而且模型实验结果还不一定具有放大性。然而,利用相似理论及量纲分析将有关物理量组合成量纲为1的特征数(相似数),就使实验工作转化为以相似数作为变量,因而实验中不必将相似数中包含的每一个物理量都作为实验测试变量,只需测量相似数中易于改变和测量的物理参数,以反映该相似数的变化就可以了。这不仅大大减少实验的次数,而且通过实验获得的量纲为1的特征数之间的关联式还可应用于生产实际。

相似原理说明两个系统流动相似必须在几何、运动和动力三个方面都要相似,然而,在采用模型实验模拟原型流动时,还需要建立相似准则才能解决问题。相似准则是流动相似的充分必要条件。建立相似准则一般有两种途径:对于已有流动微分方程描述的问题,可直接根据微分方程和相似条件导出相似准则;对于还没有建立流动微分方程的问题,只要知道影响流动过程的物理参数,就可以通过量纲分析法导出相似准则。

8.1.2.1　微分方程分析法

N -S方程所描述的黏性不可压缩流体流动的相似准则就可具体表述为:原型与模型系统中的这些相似数Re、Eu、Fr、Sr应分别相等;在此基础上,若两系统边界条件、初始条件相似,就能保证原型系统和模型系统的流动相似。

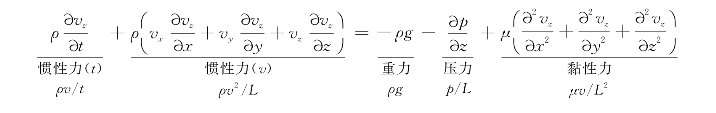
为了说明黏性不可压缩流动4个相似数的物理意义,在此先列出z方向的N-S方程

雷诺数Re(Reynolds number)　雷诺数是与流体性有关的相似数,表示惯性力与黏性力之比,即

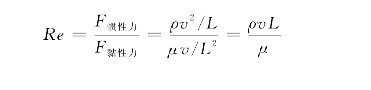
从力的角度看,该方程等号左边是单位体积流体质量(即密度)与流体加速度的乘积,因此表示的是惯性力,其中与时间变化相关的惯性力表示为ρv/t,与流体运动(空间变化)相关的惯性力表示为ρv 2/L;方程等号右边是单位体积流体受到的重力、压力(表面力)和黏性力,分别用ρg、p/L、μv/L 2表示。明确N-S方程各项的意义后,不难说明上述4个相似数Re、Eu、Fr、St的物理意义。

Re常用于分析黏性力不可忽略的流动,又称黏性阻力相似数。如果两种几何相似的流动在黏滞阻力作用下达到动力相似,则它们的雷诺数一定相等;反之,两种流动的雷诺数相等,则这两种流动一定在黏滞阻力作用下动力相似。在研究管道流动、飞行器的阻力、浸没在不可压缩流体中各种形状物体的阻力以及边界层流动等问题时,必须考虑雷诺数。

欧拉数Eu(Euler number)　欧拉数是与压力有关的相似数,因此也称为压力相似数,表示压力与惯性力之比

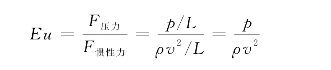
如果两种几何相似的流动在压力表面力作用下达到动力相似,则它们的欧拉数必然相等;反之,如果两种流动的欧拉数相等,则这两种流动在压力表面力作用下一定是动力相似的。欧拉数常用于描述压力对流速分布影响较大的流动,如管中的水击、空泡现象和空泡阻力问题就必须考虑。

弗劳德数Fr(Froude number)　弗劳德数是与重力有关的相似数,亦称重力相似数,表示惯性力与重力之比

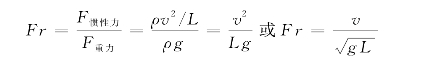
如果两种几何相似的流动在重力作用下达到动力相似,则它们的弗劳德数必然相等;反之,如果两种流动的弗劳德数相等,则这两种流动在重力作用下一定是动力相似的。在水流状态中,有急流和缓流之分,其性质很不相同。缓流中干扰微波可往上游传播,急流中则不能。弗劳德数综合反映了水流运动的惯性力作用和重力作用。当Fr>1时,水流性质为急流;当Fr<1时,水流性质为缓流。

弗劳德数常用于描述有自由表面的流动。例如,对于水力学中的港口的潮汐流动、江河的流动、堰流、孔口管嘴泄流以及流过水工建筑物等流动问题,对于液体表面的波动、船舶和水上飞机浮筒等水上运动物体的波浪阻力问题,对于在空气动力学中的具有加速度的运动物体的飞行等问题,弗劳德数有显著的意义。但对于管道内流动可不考虑此数,因为这类流动的边界为固定固体壁,边界上的速度都已经给出,不会改变。

斯特劳哈尔数Sr(Strouhal number)　斯特劳哈尔数是与时间变化相关的相似数,又称时间相似数,表示速度随时间变化引起的力与惯性力之比,即

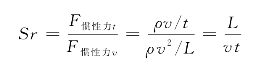
如果两种几何相似的流动在非定常流动下达到动力相似,则它们的斯特劳哈尔数必然相等;反之,如果两种流动的斯特劳哈尔数相等,则这两种流动在非定常流动下一定是动力相似的。在稳态流动时不考虑斯特劳哈尔数,但是有周期性流动时,如在研究叶片机械、螺旋桨式飞机和直升机旋翼的气动力性能时,在研究船用螺旋桨的水动力性能时,它是很重要的。需要指出的是,用时间相似准则来考虑非定常流动的模型实验,能比量纲为1的时间比尺更好地反映流动的本质。因为满足了斯特劳哈尔数,也就满足了运动相似和动力相似。

上述Re、Eu、Fr、Sr是NS方程描述黏性不可压缩流体流动的相似数。理论上,模型实验要有相似性,模型与原型两者对应的4个相似数应相等,但实践中会发现,多数情况下要做到这点是很困难的,只能根据流动问题的特点,选择保证主要的相似数相等。

除了上述Re、Eu、Fr、Sr外,对于其他不同条件下的流动,还会有另外的相似数。例如,对于高速流动,密度随压力的变化较明显,必须考虑可压缩性的影响,此时马赫数Ma (Mach number)是重要的相似数。马赫数也称为弹性力相似数,表示惯性力与可压缩性有关的力(弹性力)之比,以c表示声速,则马赫数定义为

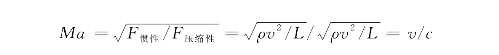
马赫准则表明,如果两种几何相似的气流在弹性力作用下达到动力相似,则它们的马赫数必然相等;反之,如果两种流动的马赫数相等,则这两种流动在弹性力作用下一定是动力相似的。通常,当气流速度大于100 m/s时,气体压缩性的影响将变得显著,如果不考虑分离或激波与边界层的相互干扰等问题,则要保证模型与原型流动动力相似,就必须保证两者马赫数相等。

当流动存在自由表面且表面张力是影响流动的重要因素时,则必须考虑韦伯数W e (Weber number)。韦伯数We表示惯性力与表面张力之比,即

We=F惯性力/F表面张力=(ρv 2/L)/(σ/L 2)=ρv 2 L/σ

此外,在以角速度ω旋转的参照系内研究流体流动时,流动微分方程中要出现柯氏力和离心惯性力,由此又可引出罗斯比数Ro(Rossby number)和埃克曼数Eo(Ekman number), Ro=v/ωL表示柯氏力与离心惯性力之比,而Eo=μ/ρωL 2则表示黏性力与离心惯性力之比。

8.1.2.2　量纲分析法

前面所讨论的是已知流动微分方程时,利用相似原理确定相似准则的方法。但工程实际中有很多问题是相当复杂的,无法建立流动微分方程,只能了解到影响流动过程的一些物理参数。对于这类问题则可通过量纲分析方法导出相似准则。

物理量的单位决定量度的数量,而量纲则指量度的性质。描述流体流动的物理量都是有量纲的量,即有单位的量。一个物理量的单位虽然可有多种,但其量纲是不变的。流体力学中最基本的物理量有长度、质量、时间、热力学温度,其量纲分别为L、M、T、Θ表示,而其他物理量的量纲则是这些基本量纲的组合,并依照习惯,用[A]表示物理量A的量纲。如面积S的量纲为[S]=[L 2],密度ρ的量纲为[ρ]=[ML-3],黏度μ的量纲为[μ]= [ML-1 T-1],速度u的量纲为[u]=[LT-1]等。对于某一物理过程,用哪些量纲作为基本量纲,取决于该过程涉及的物理参数的量纲。

只有量纲相同的物理量才能相加减,所以正确的物理关系式中各加和项的量纲必须是相同的,等式两边的量纲也必然是相同的,这就是量纲和谐原理。实验过程中,利用量纲和谐原理,对影响物理过程的各有关变量进行量纲分析,可将这些变量组合成数目较少的量纲为1的特征数,然后通过实验确定这些量纲为1的特征数之间的关系,从而大大减少实验的次数,使问题的分析得以简化。这种量纲为1的特征数之间的实验关联式还可能将小模型上的实验数据放大应用于生产实际。

量纲分析方法包括瑞利(Rayleigh)方法和白金汉姆(Buckingham)方法,具体方法可见附录Ⅻ。在采用量纲分析法时,应结合问题本身特点对已得到的相似数进行预筛选,分析哪些是主要的,哪些是次要的,既不遗漏对流动有重要影响的物理参数,也不要包括那些次要参数。当然,相似数的筛选必然要求研究者对问题本身有尽量全面的认识和了解,并借鉴前人研究工作所积累的经验。例如,在管道流动中,起决定作用的是雷诺数,而欧拉数可以忽略不计;但在研究空泡与空蚀现象时,欧拉数则是起决定作用的。