社会统计资料的整理

社会统计资料的整理_社会统计学

第二节　社会统计资料的整理

对于通过调查得到的资料，在分析前必须加以整理。否则，由于数据资料庞杂无章，往往不能从中看出问题。统计整理的中心任务就是分组和编制频数分布表。社会统计资料的整理主要包括资料的审核、资料的分组以及资料分组后的频数分析等。

一、资料的审核方法

对统计调查中所搜集的资料，在进行整理以前，还必须进行严格的审核。审核的内容主要从资料的准确性、及时性和完整性等几个方面。

检查资料的完整性，主要是检查应调查的单位有无遗漏，应调查的内容是否齐全；检查资料的及时性，主要是检查资料是否按规定时间报送，如未按规定时间报送，就需检查未按时报送的原因；检查资料的准确性，主要是检查在调查过程中所发生的误差。通常误差有两类:登记误差和随机误差。产生登记误差的主要原因是:计量错误、计算错误、抄录错误、在逐级上报过程中的汇总错误、所报不实或调查者弄虚作假，等等。这类误差是人为的，可以从提高工作人员的思想素质、业务技能和调查纪律等方面加以防止。另一类误差是随机误差，是在通过随机抽样推断总体指标时所产生的误差，故又称抽样误差。这类误差由非人为因素造成，是无法避免的，但可以应用统计推断的理论和方法加以控制。

统计资料准确性检查是统计审核的重点，检查方法有之种，即逻辑检查和技术性检查。逻辑检查是用来检查调查表或报表中的内容是否合理，有关项目之间是否矛盾的一种方法，比如14岁大学毕业、女儿年龄大于母亲、某区生产总值高于该市生产总值等。对于这种情况很容易通过计算机进行检查和纠正。但是应该注意如下两点:第一，这种方法要求检查人员熟悉情况，有一定的实际工作经验和周密的逻辑推理能力，更重要的是要坚持实事求是的科学态度；第二，发现这一类的问题不能简单地一改了之，而要通过该错误分析，分析错误原因，仔细发掘其后可能存在的类似问题，如数据输入错位问题，数据系统性误差问题等。

技术性检查主要包括:(1)填报单位有无遗漏和重复；(2)调查表有关项目是否填齐，所填内容和表格规定是否一致，有无错行或错栏情况；(3)计量单位是否和法定计量单位一致；(4)各行和各栏间数字如合计、乘积项等与分项数字是否符合，等等。

二、资料的统计分组

统计分组是根据统计研究的需要，将统计总体按照一定的标志区分为若干组成部分的一种统计方法。比如大学生总体中有很多标志，具体有年龄、性别、家庭人数、家庭经济收入、家庭所在城市、所在学校和所学专业等分组。社会现象具有多种特性，每种特性又都有内在的质与量差异，统计分组就是要把现象内部存在着质量上的差异进行区分。通过统计分组把现象内部不同性质或不同数量的单位分开，把性质相同或数量相近的单位归并在一个组内。这样就能深入地说明现象内部各组之间的相互联系及其特征。

1.分组的作用

统计分组的作用在于:(1)划分现象的类型，并反映各类型组的数量特征；(2)按照某一标志将性质不同的单位进行分组，计算各组的数量特征在总体中所占的比重，以说明现象的内部结构；(3)通过分组可以揭示现象与现象之间的依存关系，也就是说按照所研究现象的有关标志来分组可以分析该因素对另一因素的影响程度和因果关系。

2.分组的标志

在进行统计分组时，关键的问题是如何选择分组的标志和确定各组的界限。分组标志是将总体区分为不同组别的标准。一个统计总体(如学生)一般都具有多种特征(如身高、体重、生源地和年龄等)，如何根据研究问题的需要，选择出恰当的标志作为分组标志，取决于对研究目的、被研究对象认识的深刻程度，同时取决于研究者自身的修养和经验。分组的基本原则是按照不同的标志分组，体现组内的同质性和组间的差别性。为了实现这一原则就必须执行“穷尽和互斥”，穷尽是指分组不能漏掉任何一个总体单位，互斥要求每个总体单位仅属于一组，不能出现组间重叠和混淆。按照分组标志而言，有按品质标志和按数量标志分组两种。

(1)按品质标志分组

按品质标志分组就是按事物的品质特征进行分组。例如，学生总体按性别分为男女两组；学生按照专业分组、按照高考所在地分组；企业总体按所有制分为国有、股份制、外资、合资、集体和个体等组。按品质标志分组，有时个体难于归类，难于确定其具体组。有些理论上容易区分，但实际社会生活中却难于辨别，如职业和行业，再如人口按城乡分组，居民一般分为城市和乡村之组，但因目前还存在有些既具备城市形态又具备乡村形态的地区和人员，因此分组前就需慎重定义。其他部门分类、商品分类、图书分类和职业分类也都存在同样的问题。因此，在实际工作中，为了便利和统一，需要寻找合适的标准分类目录。

(2)按数量标志分组

按数量标志分组就是按事物的数量特征进行分组。如居民按家庭子女人数分组，可分为0人(无子女)、1人、2人、3人及以上；高等院校按院系数、专业数量、学生数量、教师数量等标志进行分组等等。按数量标志分组，不仅可以反映事物数量上的差别，有时通过事物的数量差异也可区分事物的性质。例如，人口按年龄分组，可以分为0～6岁、7～17岁、18～22岁、23～59岁、60岁以上；也可以分为0～14岁、15～64岁、65岁以上；还可以分为5岁一组。具体如何选择，完全取决于研究的目的，第一种分组方法可能是研究教育和就业问题，第二种方法是劳动人口划分方法，最后一种是变量比较实用常见划分方法。按数量标志分组，在确定其分组界限时，有时很困难。因此，正确选择决定事物性质差别的数量界限是按数量标志分组中的一个关键问题。比如老年人口划分标志时，我国传统采用男性60以上、女性55岁以上的退休年龄；部分发展中国家采用60岁以上人口；国际上大多采用65岁以上人口；日本则提出70岁以上人口(因为65岁以上人口比例地区差异已经不大了)，选择合适的数量标志分组，还得考虑可比性、照顾大多数研究者的划分标准。现在我国大多采用65(60)岁以上两种划分标准，60岁标准用于劳动力统计、社会保障的计算，65岁以上标准用以资料的国际比较。

3.统计分组体系

分组标志多于两个时就构成统计分组体系。有时为了研究某具体的问题，为了从不同侧面反映总体的特征，运用几个标志对总体进行分组，以形成一个完整的体系，这就是统计分组体系。统计分组体系有以下两种不同的形式:

(1)平行分组体系

如果总体按照一个标志进行分组，就称为简单分组。若对同一总体分别按几个简单标志先后进行分组，排列起来就构成一个平行分组体系。例如，人口总体分别按性别、年龄和民族等标志进行分组，若干个简单分组排列起来，就是一个平行分组体系。如按性别分组:男、女；按年龄分组:0～6岁组、7～17岁组、……、60岁以上；按民族分组:汉族组、回族组、藏族组和维吾尔族组等。其特点是每个分组样本之和分别等于总体。

(2)复合分组体系

如果总体同时按2个或2个以上的标志层叠起来分组，就称为复合分组。由复合分组形成的分组系列就称为复合分组体系。例如，对某区居民先按所在社区、再按性别、最后按居民年龄进行分类。再如，对某高校学生总体可先按学科分组，然后在此基础上再按本科或专科、性别等标志进行复合分组，其分组体系如图2.3所示。其特点是其各类个体(人数)之和等于总体数。

复合分组体系示意图

复合分组体系通过汇总可以转化为平行分组体系的相应分组，但是平行分组体系不能转化为复合分组体系。对于大样本、复杂社会现象研究适宜采用复合分组体系；相反，对于小样本、简单社会现象研究可以采用平行分组体系。一般规定，组样本量低于5的组数不宜超过总组数的30%。

三、频数分布

在统计分组的基础上，将总体中所有单位按一定标志进行分组整理，形成总体中各单位数在各组间的分布，称为频数分布或者分布数列，它是统计整理的结果。分布在各组的个体单位数称频数，又称次数或人数。各组次数与总次数之比称频率，又称比率。

1.频数分布的概念

根据分组标志特征的不同，分布数列可分为属性分布数列和变量分布数列两种。

(1)属性分布数列

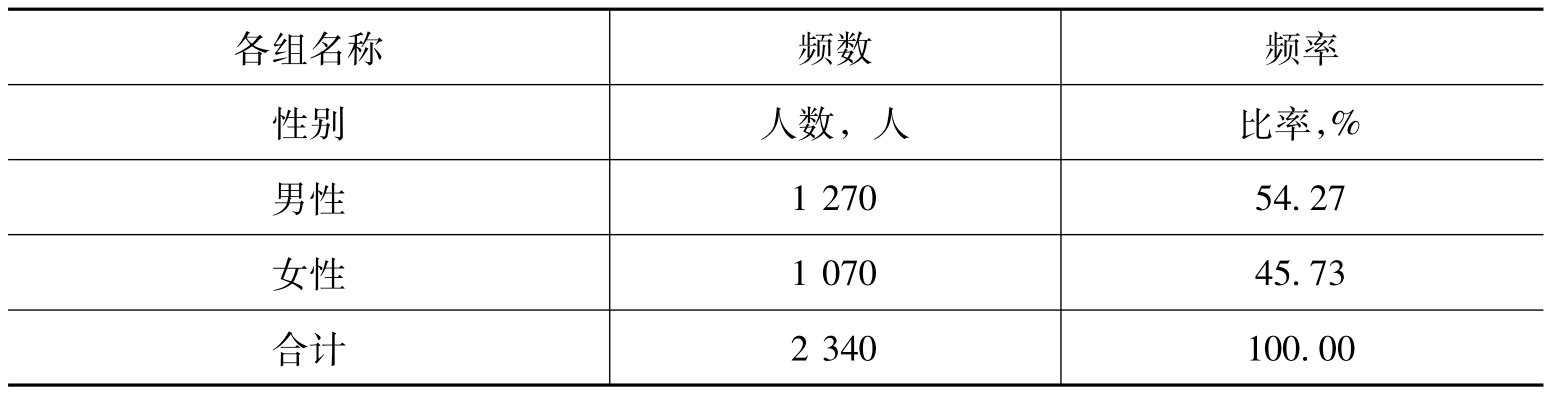
属性分布数列是指按品质标志分组所形成的分布数列，也称品质数列。例如，某大学在校学生按性别标志分组，可编成属性分布数列，如表2.2所示。

表2.2　　　　　　　　　　某大学在校学生的性别分布

(2)变量分布数列

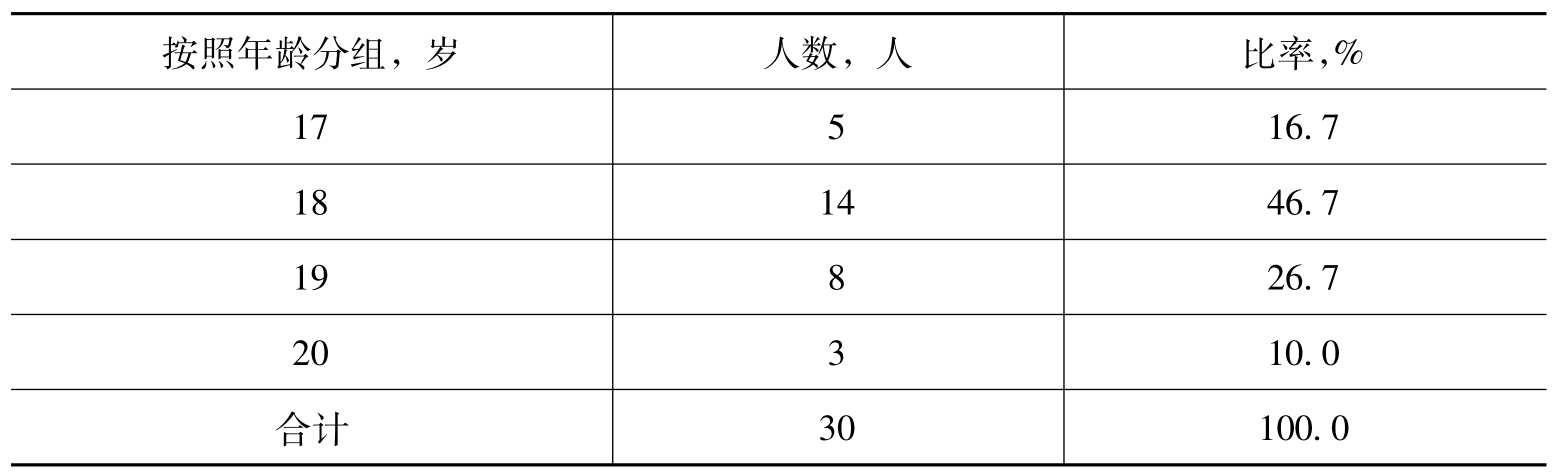
变量分布数列是指按数量标志形成的分布数列，简称变量数列。例如，某班同学按年龄分组可编制变量数列如表2.3所示。注意，年龄是按照周岁计算，是采用截尾而非四舍五入。

表2.3　　　　　　　　　　大学一年级某班同学年龄分布

对于品质数列来讲，如果分组标志选择得好、分组标准定得恰当，则事物的差异表现得就比较明确，总体中各组如何划分就较易解决。属性分布数列一般也较稳定，通常均能准确地反映总体的分布特征。对于变量数列来讲，因为分组标志往往因人的主观认识而异，因此，按同一数量标志分组时有出现多种分布数列。

变量数列按照用以分组的变量的表现形式，可以分为单项式变量数列和组距式变量数列两种，而以后者见多。

单项式变量数列是指数列中每个组的变量值都只有一个，即一个变量值就代表一组。单项式变量数列一般是在离散型变量变异幅度不大的情况下被采用的。如现在大学生大多由应届高中毕业生组成，年龄差异很小，大学新生就可用单项式变量数列表示；类似的城市职工退休年龄也可以用单项式变量数列表示。

组距式变量数列是指按一定的变化范围或距离进行分组的变量数列，又称组距数列。编制组距数列适用于变量值个数较多、变动范围较大的数据。如企业职工年龄、人们经济收入和学生成绩等。

在组距式变量数列中，组的最大变量值称为该组的上限，最小变量值称为该组的下限。上限与下限之间的距离或差数就是该组的组距，即，组距=上限－下限。组距变量数列又有等距数列和不等距数列之分，如果各组组距都相等，称为等距数列；各组组距大小不等，称为不等距(或异距)数列。

2.频数分布表的编制

(1)整理原始资料

变量数列的分组是按数量大小作为分组标准的。这样，就必须首先对原始资料加以整理，确定最大值和最小值，并计算全距，例如，某班50名学生的社会学考试成绩如表2.4:

表2.4　　　　　　　　　　某班50名学生的社会学考试成绩

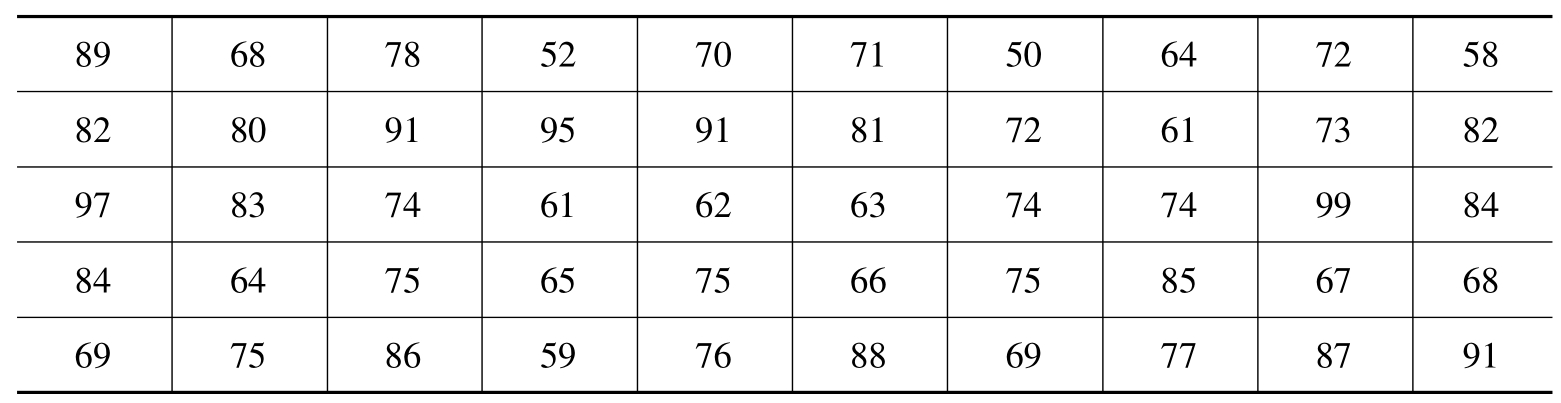
上述资料比较分散零乱，不易直接看出其基本特征。若将这些数据由小到大顺序排列(首先将这些数据排成一列，用鼠标将数据覆盖，然后选择EXCEL“数据”中“排序”，最后按确定键)，就可得到新的阵列，由重新排列的新数据阵列可看出，该班统计学原理考试成绩分布在50～99分之间，最高分为99分。最低分为50分。也可以用函数“MAX”、“MIN”求出最大、最小值。

全距=最大值－最小值=99－50=49(分)。

(2)确定变量数列的形式

对于离散型变量，因其所描述对象的数量特征，可以按一定的次序一一列举数值，相邻2个变量之间不可能有小数。例如，学生人数、拖拉机台数、废品件数和高校个数等。所以，对于这些变量，如果项数(样本)不多、变异幅度不大，可编制单项式变量数列，否则，应编制组距式变量数列。

对于连续型变量，因其所描述对象的数量特征，在一个区间内可以有无限多个数值，无法按一定次序一一列举，其变量值可以用小数表示。例如，粮食的亩产量、职工工资等等。所以连续型变量不能编制单项式变量数列，而只能编制组距式变量数列。

(3)编制组距式变量数列的其他问题

　A.确定组距。组距的大小要适度，要能正确地反映总体的分布特征及其规律。组距与组数成反比例关系，组距越大，组数就越少；组距越小，组数就越多。组数过少，容易把不同质的单位归在一个组内；组数过多，又容易把同质的单位分散在不同的组内，两者都不符合分组的要求。一般情况下采用等距分组，除非样本分布严重不均匀或有既成约定的情况应该采用不等距分组。

b.确定组限(组上限、组下限)的基本原则是，要能使性质相同的单位归入同一组内，使不同性质的单位按不同的组别划分。大多数分组要求组限，尤其是对组下限，平滑和自然，非刻意所为。

对于离散型变量，其变量值都是整数，变量值之间有明显的界线，因而，组的上下限可用肯定性的数值表示，组限非常清楚。例如，专业学科按学生人数分组，其组限可表示为:100人以下、100～499人、500～999人和1000人以上。

对于连续型变量，其变量值有小数，组限不能用肯定的数值表示，只能用前一组的上限与后一组的下限重叠的方法表示。例如，企业按职工工资分组，可以表示如下:2000元以下、2000～2500元、2500～3000元、3000～3500元、3500～4000元、4000～4500元和4500元以上。按照“上组限不在内”的原则，将达到上限值的单位划入下一组内。例如，当工资为3000元时，该单位应属第四组而不属第三组。

在连续型变量分组的表示方法中，数列的首未之组用“＊＊以下”和“*＊以上”表示的叫开口组，首、未两组的上下限俱全的叫闭口组。

组中值是上限和下限之间的中点数值，它是代表各组标志值平均水平的数值。计算组中值的公式为:

组中值=(组上限+组下限)/2

在离散组的情况下，常使用下一组的下限取代本组上限。

开口组的组距和组中值的确定，一般以其邻近组的组距为准。其计算公式为:

缺下限开口组的组中值=上限－邻近组距/2

缺上限开口组的组中值=下限+邻近组距/2

(4)频数分布表的具体编制

如前所述，某班社会学原理考试成绩的全距为49分，组距10是按照我们通常取的情况，组数一般取5组。第1组为60分以下，表示不及格；第2组为60～70分，表示及格；第3组为70～80分，表示成绩为中等；第4组为80～90分，表示成绩良好；第5组为90～100分，表示成绩优异。

社会数据的汇总方法，在的统计实践中，常用的有手工汇总和电子计算机汇总两种。

手工汇总是采用手工操作方法进行的汇总。常用的汇总方法有4种，划记法是利用点线等符号，计算各组总体单位数的一种汇总方法。常用的点线符号有“正”等。汇总时用点线符号将各总体单位数分别记入所属组中。这种方法运算简便，但不能汇总总体标志值。

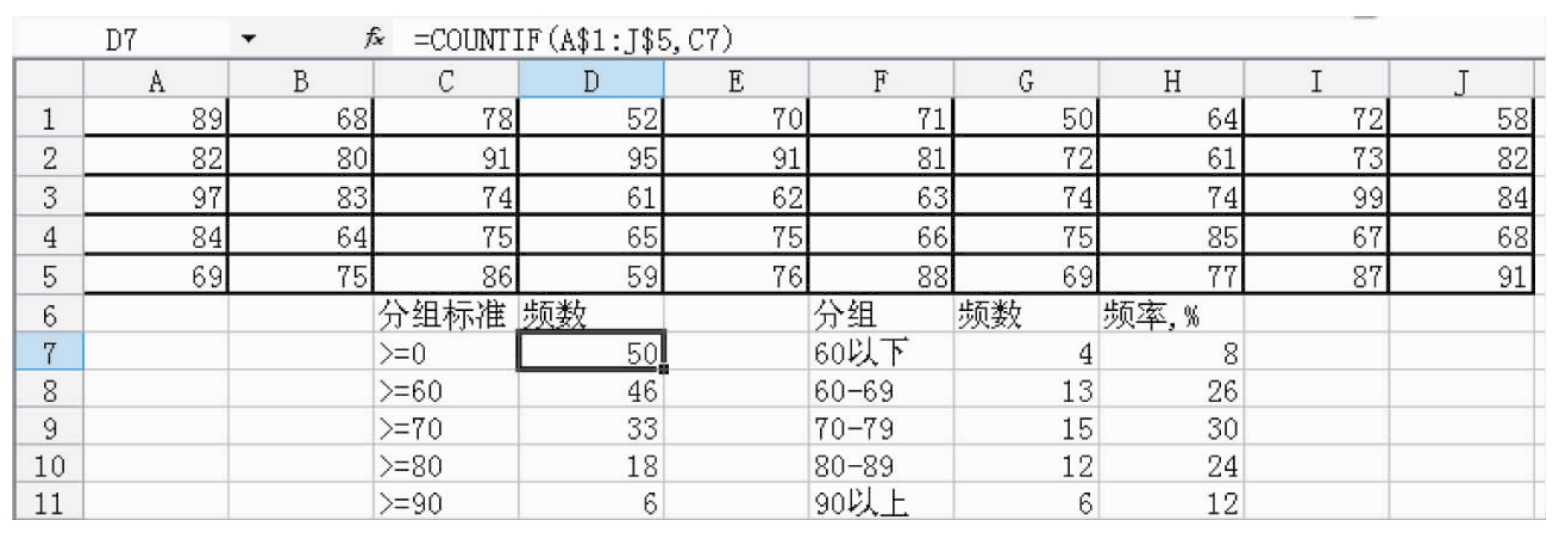
利用计算机进行统计资料的整理和汇总，是现代先进的汇总技术。主要特点是速度快、精度高；在程序控制下自动工作，进行各种逻辑判断；能储存大量的数据信息。计算机汇总技术是实现统计工作现代化的重要标志之一。这里仍以上述考试成绩为例，介绍用电脑整理编制频数分布表，打开办公软件Excel系统，将数据输入(左上角到右下角)A1到J5单元(如表2.5所示)，比如在C7到C11单元输入分组标志，在D7单元输入函数COUNTIF(条件计数)，并在其后输入参数，原始数据位置(A$1:J$5)和判据式位置(C7)，返回以后可以获得结果为50，表示大于0分的有50人；接着就可利用复制的方法，求出所有频数。

表2.5　　　　　　　　　　50名学生社会学考试成绩频数分布表