离散趋势测量法

第一节　离散趋势测量法

集中趋势表示数列的代表性数值，那么集中趋势的代表性则是用其离散趋势表示。如果2个组的平均数都是80，甲组为78、80、82；乙组为60、80、100，显然甲组平均数的代表性更好。统计平均指标是把同质总体中各个单位的数量差异抽象化，以数值的形式综合地反映总体各单位的集中趋势。变异指标则是从另外一个侧面，概括地反映总体中各单位的离中趋势分散状态或变异状况。即变异指标是用来刻画总体分布的离散程度或变异状况，变异指标值越大，表明总体各单位标志值的变异程度越大。同时变异指标可以评价平均数的代表性大小，衡量事物变动的均衡性或稳定性。标志离散标志越小，平均数的代表性越大，事物变动则越具有均衡性和稳定性。

仅仅利用描述中心趋势的统计量，不能反映整个数据集合的分布状况，具有不同分布的数据可能具有相同的算术平均值、中位数或众数等。因此，还需要统计量来反映数据与描述中心趋势统计量之间的离散状况。在统计分析中，平均指标和变异指标是互相补充，相互结合地加以运用的。总体分布的离散程度可以从不同角度、用不同方法进行考察，故描述分布离中趋势的变异指标也有多种。常见变异指标有:反映众数代表性的异众比率，反映中位数代表性的四分位差，反映算术平均数代表性的极差、平均差、标准差、方差和变异系数等。

一、异众比率

异众比率(Variation Ratio)是指非众数值的次数之和在总次数中所占的比重，用V_m0表示，其计算公式为:

V_m0=(∑f_i－f_m0)/∑f_i=1－f_m0/∑f_i　　　　　　　　　　(4.1)

异众比率主要是描述众数的代表性，但其可以测量定性数据，也可以测量定量数据的离散程度。异众比率越小说明众数的代表性越好。

如对于5个牛奶品牌和5个咖啡品牌进行300人的调查，喜欢某品牌牛奶、某品牌咖啡的异众比率分别是0.64和0.72，那说明，喜欢某品牌牛奶的集中程度更高一些，众数的代表性好。

二、四分位差

四分位差(Quartile Deviation－Q_d)是第1四分位(Q₁)和第3四分位

(Q₃)差，即:

Q_d=Q₃－Q₁　　　　　　　　　　　　(4.2)

其表示中位数的代表性，其值越小表示中位数的代表性越好。实际上，四分位差是两端各去除四分之一数据以后的极差，是对极差数据的改进，表示中间一半数据的离散程度。

三、极差和平均差

极差(Range－R)是样本数据中最大值与最小值的差值。极值舍弃了最大值与最小值之间的数据信息，仅仅依靠端点值来确定，因而稳定性差。在不分组和分组情况下，其计算公式分别为:

R=X_max－X_min　　　　　　　　　　　　(4.3)

R=最高组的上限－最低组的下限

平均差(Average Difference－A.D.)是样本数据中各数据与均值间差值绝对值的平均值，也称为平均绝对差。分组情况下的平均差可用如下公式进行计算，若在不分组的情况下，f_i=1，分母为n。

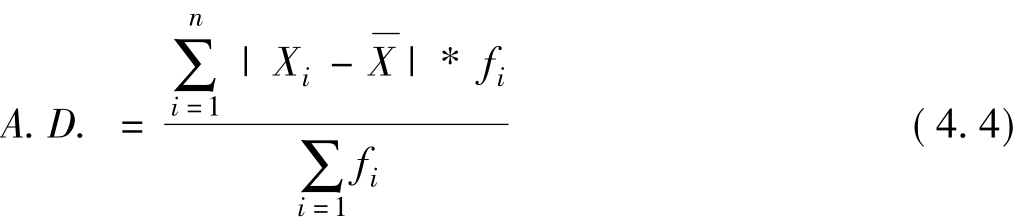
平均差含义清楚，计算结果容易理解。与极差、四分位差相比，平均差使用全部数据信息计算，全面而充分地概括反映了数据之间的离散程度。但是，平均差难以进行代数运算，尤其在计算机早期使用中，限制了平均差的应用。在统计实践中，平均差使用场合并不多。

四、方差和标准差

1.方差(Variance－σ²)

方差是各个数据与其均值的离差平方和的算术平均值，在分组情况下总体方差σ²的计算公式为:

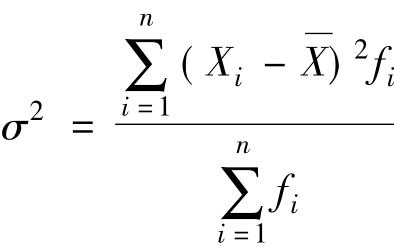
其中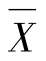，为变量X_i的平均值，f_i为相应第i组变量X_i的频数。在不分组的情况下，分子中f_i都等于1，分母为n。若将括号展开，有:

即方差等于变量平方的均值减去变量均值的平方。

2.标准差(Standard Deviation－σ)

标准差是方差的算术平方根，是最常用的反映数据离散趋势的统计量。

值得注意的是，在抽样调查中总体标准差σ²往往未知，需要用样本方差s²代替总体方差，总体方差的无偏估计量是原方差σ²乘以修正因子(N/N－1)，或者说在方差分母计算中，分组情况下用∑f_i－1替代∑f_i，或在不分组情况下用N－1替代N，并由此得到样本方差——无偏方差的估计量。样本方差s²的算术平方根是样本标准差s。

若以［例3.1］为例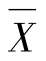，为15100元，计算方差和标准差(如表4.1所示)。

表4.1　标准差计算过程表

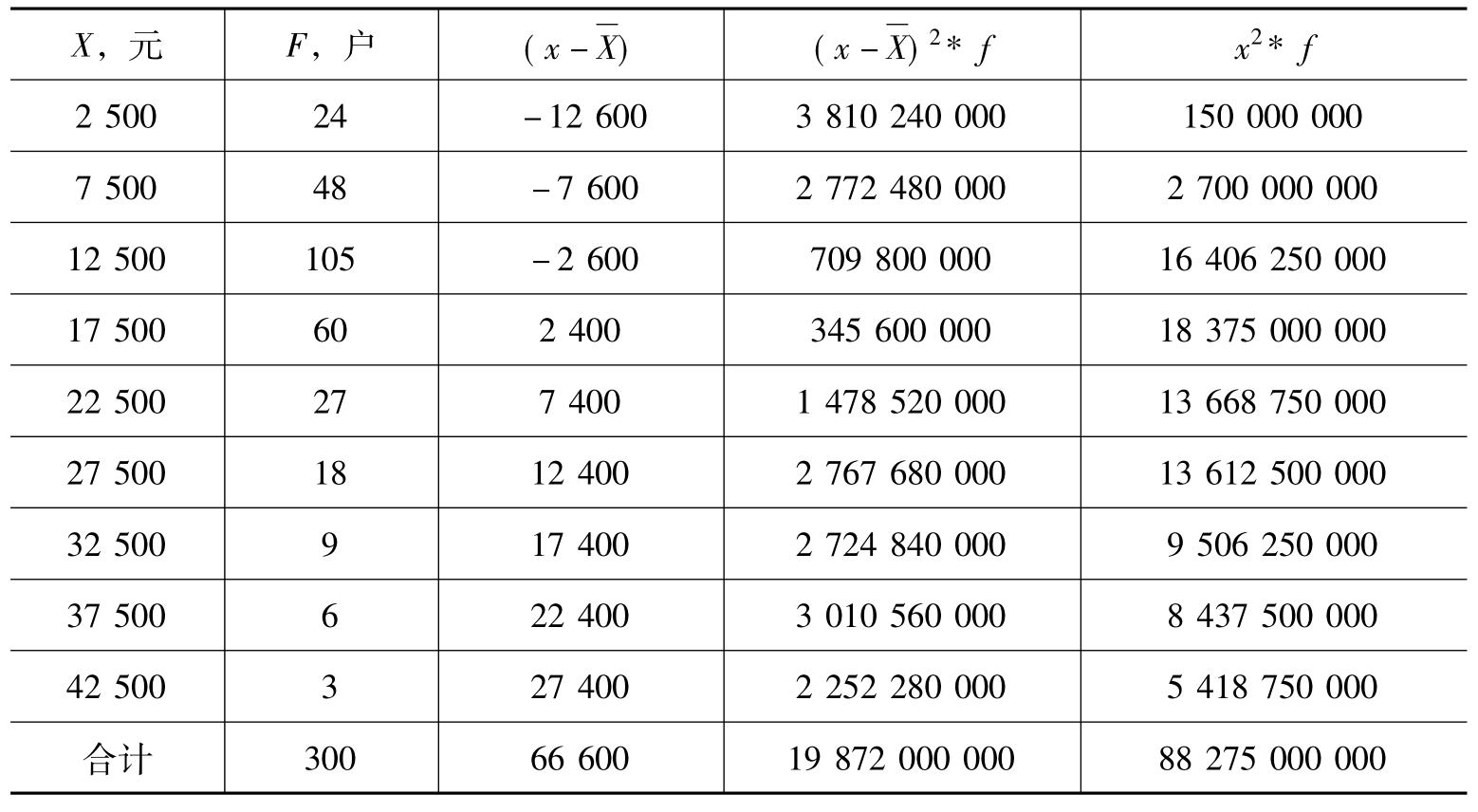
由此可见，公式4.5和4.6计算结果是完全一致。而样本方差s²= 66461538，总体标准差σ=8138.8(元)，样本标准差s=8152.4(元)。

3.数学性质

(1)常数的方差等于零。如果a为常数，则有σ_a²=0。

(2)变量的线性函数的方差等于变量系数的平方乘以变量的方差。如果a、b为常数，y=a+bx，则有σ_y²=b²*σ_x²。

4.是非标志方差

若变量属于是非标志变量，即变量的全部总体单位可划分为具有或不具有某种特征的两种分组标志的变量。如全部产品可分为合格品和不合格品，人口分为男性和女性，对某一问题的看法可分别用“是”和“否”表示等。假如具有某些特征的总体标志用1表示，其单位数为n₁；不具有某些特征的用0表示，其单位数为n₀。具有某些特征的总体单位数在全部总体单位数中所占比重用p(= n₁/(n₁+n₀))表示，不具有某些特征的总体单位数在全部总体单位数中所占比重用1－p表示。则其均值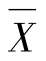方差σ_p²分别为:

X=∑xf/∑f=(1*p+0*(1－p))/(p+q)=p　　　　　　　　　　　　　(4.7)

(4.8)

［例4.1］某市200个社区中，年末检查中有10个不合格，则该市社区合格率为95%，即平均合格率为95%，合格率的方差为0.95*0.05=0.0475= 4.75%。

由于是非标志的成数p总是在0到1之间，而其方差的最小、最大值分别为0、0.25，前者是当p为0或1时，后者是当p为0.5。

五、标准化值

标准化值(Z－score)也称标准得分。对于来自不同量纲、均值和标准差的个体数据，往往不能进行直接比较或综合，这就需要将其转化为同一规格、尺度的无单位数值后再进行比较或综合。这种方法通常是将原始数据标准化，或者是将数据转化为标准化值或标准得分。标准化值一般用Z表示，其计算公式为:

其中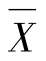、σ分别是均值和标准差。经过如此处理以后，标准得分Z_i的均值为0、标准差为1，而且变成一个无量纲的数值。于是可以进行比较分析或者可以进行综合分析了。如对学生成绩的综合评价，各教师打分的风格不一，各门课程的均值和标准差不一，平均成绩有时难以说明问题。类似地，人类发展指标(HDI)涉及人均GDP、受教育程度和出生时预期寿命等多种指标的综合评估和汇总；再如聚类分析等都用到标准化值。

标准化值是将个体指标在总体中的位置转化为其在总体中的相对位置，所以标准化值的比较仅有相对意义而没有绝对意义。

六、离散系数

前面(除异众比率外)介绍的变异指标，如全距、四分位差、平均差和标准差，都有与原有变量相同的计量单位，反映的都是总体标志数值之间变异的绝对水平。变异标志的大小不但取决于变量值差异程度，而且也受变量值水平高低和计量单位不同的影响。如学生百分制成绩的变异一般大于五分制成绩的变异。因此，在对比不同的变量水平或不同性质总体数列的变异程度大小时，不能直接用绝对量比较，而应计算反映变量值差异程度的抽象化指标。这个指标就是离散系数，又称标志变异系数。

平均差系数V_A.D.为平均差与平均数之比，标准差系数V_σ为标准差与平均数之比，其次还有四分位差系数为四分位差与中位数之比。

离散系数小，说明总体相对变异程度小；离散系数大，说明总体相对变异程度大。最常用的是标准差系数，其次为四分位差系数。