均质及非均质储层伤害试井评价模式

3．3．4．1　油气层伤害评价通式

进行油气层伤害评价的流动效率和表皮系数可以通过下列两个通式进行计算：

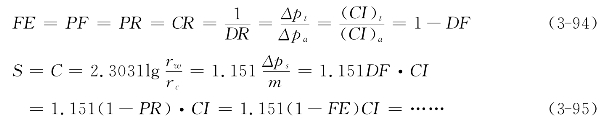
式中：C——井壁阻力系数；

　　　S——表皮系数；

　　　rc——折算半径（m）；

　　　CI——完善指数；

　　　PR——产率比；

　　　PF——完善程度；

　　　CR——条件比；

　　　m——压力恢复中间直线段斜率；

　　　DR——损害（程度）比；

　　　DF——污染系数；

　　　Δps——表皮压降（MPa）；

　　　FE——流动效率；

　　　rw——钻井半径（m）。

式中，下标t代表理想，a代表实际井，w代表井。

有了这两个通式，研究油层损害将十分方便。只要知道其中一个参数，便可利用通式求得所需要的各种表示均质、非均质地层损害的参数。这些参数评定值的范围和标准如表3－9、表3－10、表3－11所示。

表3－9　表皮系数S评价标准

表3－10　均质地层不同评定方法评价标准

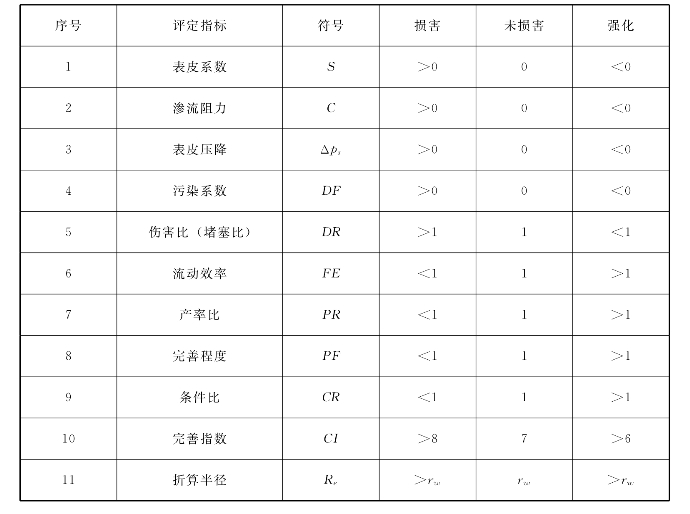
表3－11　均质油气层损害程度评价标准

上述标准和通式中的参数最有代表性的是S，如果求得S，则可知所有矿场评定地层损害的参数和标准属性。下面介绍各种条件下表皮系数的计算方法。

3．3．4．2　均质储层损害试井分析方法

无限均质地层中，考虑表皮系数时的单井系统平面径向流井底压力公式为：

利用表皮压力公式Δp＝pwt－pwf，当（T＋t／T）≈1时，可得表皮系数公式：）

取t＝1，采用法定单位，则有：

其中斜率为：

式中：h——油气层厚度（m）；

　　　B——原油体积系数；

　　　K——油气层渗透率（μm2）；

　　　μ——原油黏度（mPa·s）；

　　　q——抽气井产率（m3／d）；

　　　rw——井眼半径（m）；

　　　pwf——关井前压力（MPa）；

　　　p1hr——关井1h压力（MPa）。

可以看出，已知m，则可由式（3－98）求出S。

3．3．4．3　非均质储层损害试井分析方法

3．3．4．3．1　Pollard非均质模型

Pollard非均质模型由三部分组成，根据三部分动态，即基岩向裂缝，裂缝向损害区，损害区再向井底的流动过程的流动方程可以导出井底压力公式为：

式中：pe——地层压力（MPa）；

　　　pm——岩块的流动阻力（MPa）；

　　　pf——裂缝的流动阻力（MPa）；

　　　ps——损害区的流动阻力（MPa）；

　　　a——压力衰减系数。

下标m、f和s分别代表岩块、裂缝和损害区。当t＝0时，式（3－100）变化为：

当地层未受到损害时，ps＝0；当地层受到损害时，ps＞0；而当ps＜0时，地层被强化。也可以用损害区阻力损失所占比例表示损害程度，损害百分比：

Rs愈大井底损害愈重，反之亦然。当Rs＝0时，未损害。Pollard法精度差，当测试时间短时误差将更大。

3．3．4．3．2　Bourdet－Gringarten双重介质模型

在双重介质油藏中，可以由均质油藏中一口具井筒储存和表皮效应井的典型曲线与双重介质油藏中一口井的典型曲线叠加而成。其表皮系数的计算或拟合如下：

其中

（CDe2s）f＋m由曲线拟合对比得到：

式中：V——油气层体积。

根据CDe2s值还可以对双重介质油藏完井系统地层损害进行定性的资料分析：

损害井（CDe2s）f＞103，未损害井（CDe2s）f＝103～5；

酸化井（CDe2s）f＝5～0．5，压裂井（CDe2s）f≤0．5。

3．3．4．3．3　de Swaan－O和Serra双重介质层状模型

Serra等在de Swaan－O层状模型基础上建立起裂缝型油层三个相互区别的半对数直线段流动过程。中期直线斜率几乎是早、晚平行线斜率的一半。晚期直线开始时tDb3＝3．7ωD／λDωD≥λDωD≤10－3时，中期直线开始和结束时间分别为tDb2＝380／λDωD、tDe2＝0．63ωD／λD。利用早期直线段分析方法，两线交点对应时间为：

中晚期直线交点对应时间为：

其中n＝h／hm，ω为岩块弹性容积比，λ为裂缝串流系数，下标b代表开始，e代表结束，f代表总的，时间单位为h。倘若出现两个或两个以上的流动过程，相应过程可以通过其直线斜率的大小来识别，早中晚各阶段的S如下：

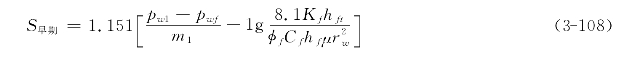
其中下标1代表早期直线，2代表中期直线，3代表晚期直线，wf代表井底流动。

如果ωD较大而λD较小时，则只有中期直线段出现（不过延长测试时间可以得到晚期直线段），而ωD较小λD较大时，则仅有晚期直线段出现。在这种情况下当不能正确地鉴别直线斜率时，将导致计算的S值是错误的。而且，在应用中间直线段时还要求已知岩块的物性参数。尤其要注意，m2＝0．5m的条件是：层状ω≤5×10－2，球状ω≤10－2。否则：

3．3．4．3．4　Bourdet双重介质压力导数曲线

压力导数曲线有放大双重介质微弱信息的功能，能清楚地给出三种流动特征状态范围，明确显示双重介质油层的非均质特征。由于匹配是在单一曲线内进行，拟合具有唯一性，所以能正确估算S值。拟合计算公式如下：

但压力导数方法并非万能，当多变产量试井时，对于非均质地层的流动曲线形状将发生显著的失真，或不出现稳定曲线段，导致选择拟合参数点和计算S值时出错。