3.3.1 资金等值的概念
由前述已知，资金具有时间价值。即相同的金额，因其发生的时点不同，其价值就不相同；反之，不同时点绝对值不等的资金在时间价值的作用下却可能具有相等的价值。
资金等值是指与某一时间点上的金额实际经济价值相等的另一时间点上的价值。例如，将1 000元钱存入银行，年利率为3%，一年后可取出1 030元。由此可知，一年后的1 030元与现在的1 000元钱是等值的。
在工程经济分析中，资金等值是一个十分重要的概念，它为我们提供了计算某一经济活动有效性或者进行方案比较、优选的可能性。
影响资金等值的因素有资金的数额、资金发生的时点及一定的利率。反映在资金等值基本计算公式上的几个基本概念主要包括：
折现（贴现）：把将来某一时点上的资金金额换算成现在时点的等值金额的过程。
现值：折现到计算基准时点的资金金额。
终值：与现值相等的将来某一时点上的资金金额。
折现率：折现时的计算利率。
3.3.2 资金等值的计算方式
利用资金等值的概念，把不同时点上发生的资金金额换算成同一时点的等值金额，这一过程叫做资金等值计算。资金等值的计算方法与利息的计算方法相同，根据支付方式不同，可以分为一次支付系列、等额支付系列、等差支付系列和等比例支付系列。
本书主要介绍一次支付系列和等额支付系列。
进行资金等值系列计算时，公式中的基本假设条件是：
（1）项目的期初投资P发生在现金流量图的0点。
（2）本期的期末为下期的期初。
（3）A和F均在期末发生。
1.一次支付系列
一次支付又称整付，是指所分析系统的现在流量，无论是流入还是流出，均是一次性发生的。
（1）一次支付终值（Future Value）公式（已知P，求F）。
其经济含义是期初发生的一笔资金P，经过n次计息后的价值是多少。其中(1+i )n又被称为一次支付终值系数，用(F/P,i,n)表示，因此式（3-6）也可以表达为
公式中各符号含义同前，现金流量如图3-2所示。
图3-2 一次支付终值公式的现金流量图
【例题3-4】 某人年初借本金1 000元，年利率为3%，借款期限5年。试求5年后该人应还的本息和。
解：利用公式（3-6）可得
也可利用公式（3-7）计算，查复利系数表得
（2）一次支付现值（Present Value）公式（已知F，求P）。
公式（3-8）可由公式（3-7）推导出。其含义是n年后的一笔资金F，折算成现在的价值是多少。(1+i)-n 又被称为一次支付现值系数，用(P/F,i,n)表示，因此上式也可以表达为
在复利系数公式中，括号内斜线上面的符号表示未知的，斜线下面的符号表示已知的。一次性支付现值公式的现金流量图如图3-3所示。
图3-3 一次支付现值公式的现金流量图
【例题3-5】 某企业计划建造一条生产线，预计5年后需要资金1 000万元，设年利率为10%。现需要向银行存入多少资金？
解：利用公式（3-8）可得
利用公式（3-9）计算，查复利系数表得
2.等额支付系列
等额支付系列是多次收付形式的一种。多次收付是指现金流不是集中在一个时点上发生，而是发生在多个时点上。现金流量的数额大小可以是不等的，也可以是相等的。当现金流大小是相等的，发生时间是连续的，就称为等额支付系列，其现金流量又叫做年金（Annuity）。
（1）等额支付系列终值公式（已知等额年金A，求年金终值F）。
式中，
称为等额支付系列终值系数，亦可使用(F/A,i,n)来表示。因此上式又可被记作：
该公式的含义是指在一个时间系列中，在利率为i的情况下，连续在每个计息期末支付一笔等额的资金A，在n个计息期后的本利和F应为多少。公式推导如下：
第一年的本利和：
第二年的本利和：
第三年的本利和：
⋮
第n年的本利和：
利用等比级数求和公式得
公式的现金流量图如图3-4所示。
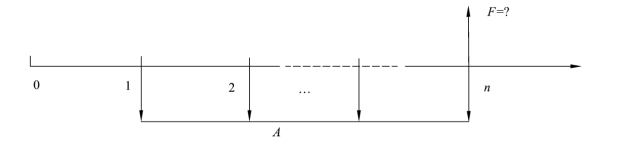
图3-4 等额支付系列终值现金流量图
【例题 3-6】 某单位在大学设立奖学金，每年年末存入银行2万元，若存款利率为3%。第5年末可得款多少？
解：利用公式（3-10）可得
也可列为
（2）等额支付系列偿债基金公式（已知年金终值F，求等额年金A）。
本公式可由公式（3-10）推导得出，式中
称为等额支付系列偿债基金系数，亦可用(A/F,i,n)来表示。因此上式也可以被记作：
该公式的含义是为了筹集未来n年后需要的一笔资金F，在利率为i的情况下，每个计息期末应等额储存的金额A是多少。其现金流量图如图3-5所示。
图3-5 等额支付系列偿债基金现金流量图
【例题 3-7】 某厂欲积累一笔福利基金，用于 3 年后建造职工俱乐部。此项投资总额为200万元，设利率为5%。每年末至少要存多少钱？
解：利用公式（3-12）可得
也可列为
（3）等额支付系列年金现值公式（已知等额年金A，求年金现值P）。
在公式（3-8）中，因为P=F×(1+i)-n ，所以由公式（3-10）可推导出等额支付系列年金现值公式：
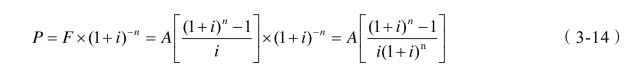
公式（3-14）中，
称为等额系列年金现值系数，记作(P/A,i,n)。因此公式（3-14）亦可写成：
公式（3-14）的含义是在年利率为i的情况下，在n年内每年等额收入一笔资金A，则此等额收入的现值总额P应为多少。其现金流量如图3-6所示。
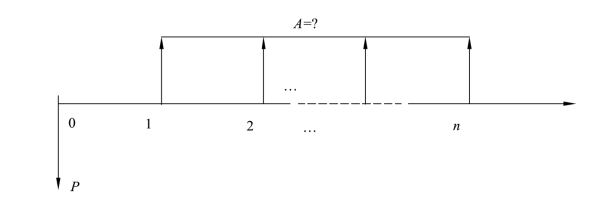
图3-6 等额支付系列现值现金流量图
【例题3-8】 某人贷款买房，预计他每年能还贷2万元，打算15年还清，假设银行的按揭年利率为5%。其现在最多能贷款多少？
解：利用公式（3-14）可得
也可由
（4）等额支付系列资金回收公式。
等额支付系列资金回收计算是等额支付系列现值计算的逆运算，故其计算公式为
式中，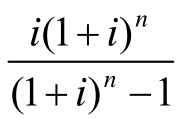
称为“等额系列资本回收系数”，记作(A/P,i,n)，故该式又可写成：
公式（3-16）的含义是期初一次性投资数额为P，欲在n年内将投资全部收回，则在年利率为i的情况下，每年等额回收的资金A为多少。其现金流量图如图3-7所示。
图3-7 等额支付系列资金回收现金流量图
【例题3-9】 某投资人投资20万元从事出租车运营，希望在5年内收回全部投资，若折现率为15%。平均每年至少应收入多少？
解：利用公式（3-16）可得
也可列为
3.3.3 名义利率与实际利率
在复利计算中，利率周期通常以年为单位，它可以与计息周期相同，也可以不同。当利率周期与计息周期不一致时，就出现了名义利率和实际利率的区别。
1.名义利率
所谓名义利率r，是指计息周期利率i乘以一个利率周期内的计息周期数m所得的利率周期利率，即
若月利率为 1%，则年名义利率为 12%。很显然，计算名义利率时忽略了前面各期利息再生的因素，这与单利的计算相同。通常所说的年利率都是名义利率。
2.实际利率
若用计息周期利率来计算利率周期利率，并将利率周期内的利息再生因素考虑进去，这时所得的利率周期利率称为利率周期实际利率，又称为有效利率。
设名义年利率为r，在一年中计息m次，则每一计息周期的利率为r/m。若年初借款为P，则一年的本利和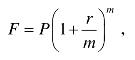
利息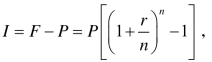
则实际年利率为
式（3-19）也称作离散式复利的名义利率和实际利率的转换式。
3.名义利率和实际利率的关系
为了进一步说明名义利率和实际利率之间的区别与联系，我们以名义利率为10% 为例，分别计算按年、半年、季度、月、日连续计算复利，其相应的实际利率见表 3-1。从表 3-1中可以看出，每年计息期m越多，i与r相差越大。
表3-1 名义利率与实际利率的关系
通过上述分析与计算，可知名义利率与实际利率间存在着下述关系：
（1）当计息周期为一年时（m=1），名义利率与实际利率相等（i=r）。
（2）当计息周期少于一年时（m＞1），实际利率大于名义利率（i＞r）；名义利率越大，周期越短，实际利率与名义利率的差值就越大。
（3）当计息周期m→∞时，即为连续复利，表示在1年中按照无限次计息，则有
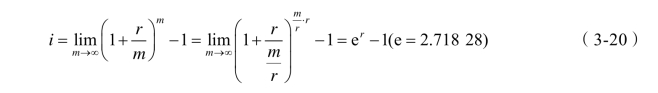
由式（3-20）可见，连续计息期内的有效年利率i趋向于一个极限，但并非无限大。
（4）名义利率不能完全地反映资金的时间价值，实际利率才能真实地反映资金的时间价值。
3.3.4 资金等值计算的应用
资金时间价值是工程经济分析的基本原理，资金等值计算是这个原理的具体应用。在进行计算时要注意严格按照基本公式应用的条件进行套用，不能直接应用公式时，可以进行适当的变换，使其符合基本公式。在变换过程中，常常用到名义利率和实际利率。
1.计息期与支付期一致的计算
【例题3-10】 某企业有一笔投资，打算从17—20年的年末收回1 000万元。若年利率i＝10%，则此投资的现值是多少？
解：现金流量图如图3-8所示：
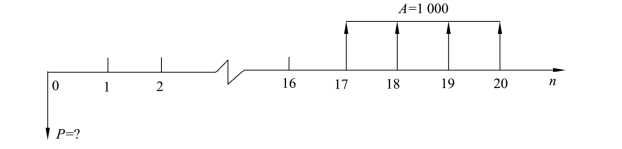
图3-8 现金流量图
方法一：根据一次支付现值公式计算：
方法二：先根据等额支付现值公式将年金折现到17年年初，再根据一次支付现值公式折现到0年的现值：
2.计息周期小于（或等于）资金收付周期时的等值计算
当计息周期小于（或等于）资金收付周期时，等值的计算方法有以下两种：
（1）按收付周期实际利率计算。
（2）按计息周期利率计算，即
【例题3-11】 现在存款1 000元，年利率10%，半年复利一次。问：5年末存款金额为多少？
解：第一种方法：按年实际利率计算：
第二种方法：按计息周期利率计算：
3.计息周期大于收付周期
由于计息周期大于收付周期，计息周期间的收付常采用下列三种方法之一进行处理。
（1）不计息。在工程经济分析中，当计息期内收付不计息时，其支出计入期初，收益计入期末。
（2）单利计息。在计息期内的收付均按单利计息。
【例题3-12】 付款情况如图3-9所示，年利率8%，半年计息一次，复利计息，计息期内的收付款利息按单利计算（单位：万元）。问：年末金额多少？
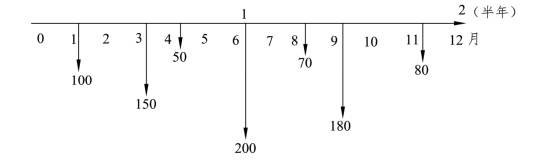
图3-9 现金流量图
解：计息期利率i=8%/2=4%，计息期内的收付款利息按单利计算：
然后利用普通复利公式即可求出年末金额F为
（3）复利计息。
计息期长于支付期。以存款为例，通常规定存款满足计息期时才计利息，既在计息期间存入的款项在该期不计息，要到下一期才计利息。因此，在计息期间存入的款项，相当于在下一个计息期初的存入；在计息期提取的款项，相当于在前一个计息期末的支取。
【例题3-13】 有一项财务活动的现金流量图如图3-10所示（箭头向上表示存款，箭头向下表示取款，单位：万元）。如果年利率为 12%，按季度计息，则这个现金流量年末的终值F是多少？
图3-10 财务活动现金流量图
解：由于计息期为每季度，且计息期内不计息，因此，将现金流量合并到每个季度的期末，合并整理后的现金流量图，如图3-11所示。
图3-11 财务活动整理后现金流量图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
