【摘要】：Prony算法用指数函数的线性组合来估算等间距采样信号中各频率成分的幅值、频率、衰减因子和初相位。正是由于这一特点，该算法在电力系统的响应信号分析中已获得初步的研究成果并显示出良好的应用前景。特别在电力系统低频振荡模态提取方面，Prony算法提供了一种全新的手段，具有相当好的实用性。对于给定的振荡信号y，有式中)是y的估计，p为模型阶数，Ai为幅值，fi为频率，αi为衰减因子，φi为初相位。Prony方法拟合的离散形式为
Prony算法用指数函数的线性组合来估算等间距采样信号中各频率成分的幅值、频率、衰减因子和初相位。正是由于这一特点，该算法在电力系统的响应信号分析中已获得初步的研究成果并显示出良好的应用前景。特别在电力系统低频振荡模态提取方面，Prony算法提供了一种全新的手段，具有相当好的实用性。
Prony算法可用指数函数的线性组合来拟合等间距采样的信号，并能估计出信号中各频率成分的幅值、频率、衰减因子以及初相位。对于给定的振荡信号y(t)，有
式中
)是y(t)的估计，p为模型阶数，Ai为幅值，fi为频率，αi为衰减因子，φi为初相位。Prony方法拟合的离散形式为
式中，bi=Aiexp(jφi)，zi=exp[(αi±j2πfi)Δt]。
按照最小二乘，即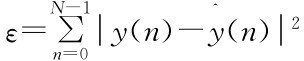
最小可估算出所求信号的特征值。为此，这是一个求解非线性的最小二乘问题。
若将zi看成线性常系数差分方程的根，则有
又
因此
则真实的测量信号y(n)为近似值
与差值e(n)之和，即
定义
其中，r(i，j)=
y(n-j)y(n-i)，i，j=0，1，…，p
求解方程(2-8)，可以得到系数α1、α1、…、αp，然后由特征方程式
φ(z)=zp+α1zp-1+…+αp-1z+αp=0 (2-9)
得特征值zi(i=1，2，…，p)，则可求出处理信号的衰减因子和频率
进而根据式(2-5)求出bi，则处理信号的幅值和初相位为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
