反演变结构自适应阻尼控制器设计

5.2.1.1 多机电力系统数学模型

由n台发电机组成的互联多机电力系统，第i台发电机的三阶模型为

变量和参数的下标i是互联电力系统中机组的编号，i=1，2，…，n，且Pei为第i台发电机的电磁功率(p.u.)；Idi和Iqi为第i台发电机的定子电流，即

式中，xdi和x′di分别为第i发电机的d轴同步和暂态电抗(p.u.)；xqi为第i台机组的q轴同步电抗(p.u.)；δij是第i和j台机组的相对功角；Gii和Bii分别为第i台机组的自导纳，Gij和Bij分别为第i和j台机组间的互导纳。

为了将式(5-1)进行精确线性化，首先，令

然后，根据精确化知识，对式(5-5)进行求导可得

其中:

将式(5-7)代入式(5-6)中得到

其中:

其中:

5.2.1.2 阻尼控制器设计

在多机电力系统中进行自适应阻尼控制器的设计，是一个3n阶系统，对于每一个确定的i，可以单独设计，其非线性方程如下

其中:xi=[x1i，x2i，x3i]T为状态变量；fi(x)，gi(x)为非线性函数；ui为控制量；ϑi(x)为充分光滑函数且已知；θi为不确定参数；输出变量为x1i。其反演变结构自适应控制器设计需要3步，在最后一步中根据来确定变结构控制及参数估计算法。

第1步

取zi1=xi1，z2i=x2i+αi1，

则=z2i-α1i 　(5-13)

定义Lyapunov函数V1i=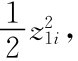

则=z1iz2i-z1iα1i 　(5-14)

令α1i=c1ix1i=c1iz1i(c1i＞0)

则=-c1iz21i+z1iz2i 　(5-15)

当z2i=0时系统是稳定的。

第2步

取z3i=x3i+α2i，

则 　(5-16)

定义Lyapunov函数V2i=V1i+1 2

z22i，

则=-c1iz21i+z1iz2i+z2i(z3i-α2i+)　(5-17)

令α2i=c2iz2i+z1i+(c2i＞0)，

则=-c1iz21i-c2iz22i+z2iz3i 　(5-18)

当z3i=0时系统是稳定的。

第3步

引入变结构控制，定义滑动面为

δ=k1iz1i+k2iz2i+z3i 　(5-19)

式中，k1i＞0，k2i＞0，

则 　(5-20)

由式(5-12)～(5-18)得

从而，有

构造Lyapunov函数为

其中，ri＞0，为自适应增益系数，则

采用指数逼近律=-hi[σi+βisgni(σ)]，其中，hi＞0，βi＞0，这是一种具有良好品质并且简单的趋近律。选择适当的hi，βi的值，可适当提高动态品质。

从而可得反演变结构控制规律为

其中是对θi的估计值。

该控制器就是通过调整励磁电压Efi来改善系统的阻尼特性，通过构造反演变结构控制规律，使得系统在受到扰动后，输出变量能够渐进跟踪初始的平衡点，最终达到全系统渐进稳定，其结构图如图5.1所示。

图5.1 反演变结构自适应控制器结构图

从以上的分析可知，该控制器有如下特点:

1)控制量励磁电压Efi只与发电机本身的参数有关，与输电网络参数无关。所以，该控制器对电网参数及电网结构的变化具有完全的自适应能力。

2)设计过程中充分考虑了不确定性参数发电机阻尼系数D，该控制器对系数D进行实时估计，使得在系数不精确的情况下有良好的控制效果。

因此，利用反演变结构规律设计的控制器既有自适应能力，又具有很强的鲁棒性。