可调螺距螺旋桨流体动力设计的一些问题

报告主旨

与常规螺旋桨一样，按船舶推进要求，选定调距桨的参数（直径、螺距、翼型剖面等）。但为适应实船航行中船体有效功率和主机输出功率—转速等的变化，推出了可调螺距螺旋桨，即令桨叶绕转叶轴旋转，改变桨叶与水流相对角度——“调节螺距”，以改善航行条件变化后的船—机—桨匹配。为此，要调节桨叶柄在桨毂座内的相对位置，出现了新的问题，在桨吸收主机功率和发出船航行所需推力条件下，如何固定和调节桨叶柄在毂座内的位置。为此，要了解桨叶受到的流体动力，包括桨叶调节时的情况。

1 桨叶绕转叶轴的力和力矩

在定距桨强度校核时，需要知道桨叶r S处剖面的力和力矩，算出桨叶剖面的应力和评估其强度；调距桨叶也要进行同样的强度评估，但所述力和力矩要经桨叶柄和桨毂传到桨轴及船体上，要保证桨叶在毂座内的位置固定和可调节。照理，计算桨叶面上的流体压力和阻力分布，积分求出整片桨叶所承受的合力及相对转叶轴的力矩，也可通过模型试验测定所述力和力矩。随着螺距的变化（桨叶绕转叶轴调节），桨叶的绕流及流体动力情况非常复杂，模拟、测试及计算有问题。工程上，首先要对转叶力矩的量级有一个评估，从而确定转叶机构固定和调节时受到的力，设计恰当的转叶装置，保证其机械动作和强度。

图1 桨叶受力及转叶力矩示意

为此，假定已知螺旋桨的推力T和扭矩Q，桨的推力和扭矩平均分配到每片桨叶上，每片桨叶分摊到1/Z的推力和扭矩（Z为桨叶数）。若桨叶所承受的流体表面力的合力处在r S半径处的G点上。图1为r S半径圆柱面上剖面的展开，为评估调距桨运行过程桨叶绕转叶轴的力矩的量级，近似认为在圆柱面内绕转叶轴的作用力矩，就是在垂直转叶轴的平面内的力矩值。作用于桨叶的推力T/Z及分摊到桨叶的扭矩Q/Z作用于r S半径处的同向力为。转叶轴通过“O”点，垂直图面，合力作用点为“G”点，距桨转叶轴—桨轴平面的距离为“e”，距桨盘面为“f”，则转叶力矩为Mb

计及桨叶剖面螺距角γ及G点距转叶轴“O”的距离OG，有：

e=OG·cosγ，f=OG·sinγ

图1所示OG为正值，即合力作用点由转叶轴往桨叶导边偏移，在图示力的作用下，其转叶力矩Mb若导致桨叶往螺距角增大方向转动，则为正转叶力矩。反之，为负转叶力矩。桨叶合力作用点G与转叶轴的相对位置确定桨转叶力矩的方向，为保证桨叶在设定位置运行，转叶机构必须提供力矩，以平衡所述流体动力转叶力矩Mb。

通常由快速性计算已知船舶运行时整个螺旋桨的推力T及扭矩Q。若表示桨叶合力作用点G到转叶轴的距离OG=h，该合力作用点所在剖面的螺距角为γ，计及表达式T=KTρn2D4、Q=KQρn2D5，可将式（1.1）写成：

常见桨的合力作用半径r S≈0.65，计及，代入上式，得：

表示转叶力矩系数CM=Mb/ρn2D5，则有Mb/Q=CM/KQ。

现若以常见中高速船用调距桨为例，JP≈1.0，ηP≈0.68，γ≈31.5°（P/D≈1.25），则可得近似关系式CM=。由此可见，要减小桨叶的转叶力矩，便于调距桨的控制，应减小h值，即转叶轴接近桨叶合力中心。可惜，同一桨叶在不同螺距角位置合力作用中心点是“漂”动的。因此，实际运行时桨叶可能受到不同大小和方向的转叶力矩，需要桨转叶机构应对。

早在采用可调螺距空气螺旋桨时，由于其桨叶宽C与桨径D之比C/D≈0.05，叶宽沿径向变化也不大，h/D数值较稳定，h/D值可取得较小，从而控制了转叶力矩Mb，轻便地实现了调距任务。船用螺旋桨叶宽C与桨径D之比C/D≈0.35～0.45，而且叶宽沿径向变化显著，桨叶绕转叶轴转动，可能导致h值在弦长C的20%长度范围内变动，出现h/C=0.2。即桨叶合力作用中心到转叶轴的h/D≈0.07～0.10之间，实际船用调距桨的转叶力矩系数CM=≈（0.37～0.51）KQ/Z。计及大多数实用桨的高效率ηP区的KQ≈0.035～0.045，则对于Z=4和Z=5的螺旋桨，有CM≈0.0026～0.0057。从1968年苏联出版《可调螺距螺旋桨流体动力学》的英译本及20世纪90年代获得的俄罗斯试验资料看，工程实践中遇到的转叶力矩系数CM的数值在±0.005之间。

由于单一桨叶的转叶力矩Mb与整桨的运行扭矩Q的比数Mb/Q=CM/KQ值在1/7到1/9左右，为调控单一桨叶在指定状态运行，需要转叶机构提供相应锁住桨叶柄的力矩，与转叶力矩大小相等、方向相反。为此，考察一下转叶力矩的实际数值。

取直径D=4.2m桨为例，以230r/min航行时，桨吸收功率为PD=18000k W，扭矩Q=PD/2πn=747k N·m；以175r/min航行时，PD=7600k W，扭矩Q=414k N·m。又如D=1.85m桨，以342r/min航行时，PD=2100k W，扭矩Q=58.6k N·m；以255r/min航行时，PD=680k W，扭矩Q=25.5k N·m。若两桨的转叶力矩与桨扭矩之比Mb/Q=1/8。则有D=4.2m桨以全速航行时，转叶力矩Mb=93.4k N·m，以中速航行时，Mb=51.8k N·m。而D=1.85m桨以全速航行时Mb=7.3k N·m；以中速航行时，Mb=3.2k N·m。可见调距桨运行时，都要用可观的力矩锁住桨叶，才能保持桨叶在设定螺距状态运行。实际D=4.2m桨的叶柄盘直径d=600mm，采用曲柄式转叶机构，曲柄销（crankpin）中心距转叶轴中心距离l≈200mm，为平衡转叶力矩、制动桨叶，曲柄销需承受横向剪力F=Mb/l，数值在（470～260）k N之间，可见转叶机构处在非常紧绷的状态运转。

2 调距桨叶转叶轴选择

桨叶转叶力矩的大小，影响转叶机构的张弛，为保证机构的灵巧，希望转叶力矩值能小点，即桨叶流体动力合力作用中心能处在转叶轴上，轻轻推拉曲柄销，即能实现桨叶调距。由于桨叶调距后合力作用点的“漂”动，以及转叶力矩与桨所运行的吸收功率（扭矩）同步增大，通常设计工况桨的吸收功率最大，故转叶轴的选定，主要考虑桨在设计工况时的需要。

在选择转叶轴位置时，有两种思路。如图1所示，若合力作用点G在转叶轴O点到桨叶导边之间，则转叶力矩为正，在该力矩作用下，桨叶自动往螺距增大方向转，则桨的扭矩及推力都增大，照理要到极限位置或主机无法提供需要的拖动力矩为止。相反，若G点在转叶轴O点到桨叶随边之间，则转叶力矩为负，在该力矩作用下，桨叶将往螺距减小方向转，桨的扭矩及推力将减小，桨吸收功率减小，从动力机器运行角度看，趋向安全。为保证桨叶螺距调控，只需将曲柄销“顶”在预设位置。由于OG=h的绝对值较大，转叶力矩较大，整个转叶机构可能比较笨重，这是一种思路。还有，就是让转叶轴尽量接近合力作用中心，令OG=h→0，则转叶力矩很小，易于进行调控，由于船用螺旋桨所处流场（船后伴流场）的不均匀性，每片桨叶在不同周向位置的合力作用点出现“漂”动现象，转叶力矩忽正忽负，转叶机构必须既“顶”住，又“拉”住曲柄销。整个转叶机构运行相对复杂，但承受的转叶力矩相对小，转叶机构可能比较灵巧，这是第二种思路。在20世纪60年代前后，开发船用调距桨的先行国家，利用上述两种思路的都有。当时采用的桨叶大多是导边—随边宽度对称的分布。

从20世纪80年代起，为减震、降噪等目的，出现侧斜螺旋桨，桨叶各半径剖面沿周向移动，从而导致桨叶合力作用点的位置变动幅度加大；由于侧斜还导致桨叶绕转叶轴调控后，空间位置变化幅度也更大。因此，要确定调距桨叶在各螺距位置的流体动力合力值和作用中心（包括转叶力矩），无论是用模型试验测定，还是理论计算方法，都有困难。问题在于各种调距角位置时桨叶流体动力模拟及数学模型建立，在此只是对问题做点物理说明。工程实践的需要，还是促成了船用侧斜调距桨工业产品开发取得了目前的进展。

与定螺距螺旋桨相似，通常调距桨的侧斜度在45°以内，桨叶剖面螺距、侧斜角的径向分布规律相似，即由桨毂起内半径剖面先向前（导边）侧斜θsk＞0，逐步转到外半径向后侧斜θsk＜0。按各国船检规范关于侧斜角的定义规定，为剖面中点到桨轴心连线与桨叶参考线的桨盘面上投影夹角。只是在调距桨情况下，通常转叶轴线就是桨叶参考线。最大侧斜角与最小侧斜角之差为桨叶侧斜度，选择的侧斜角θsk沿径向的变化，导致的桨外形轮廓是光顺的。关于桨叶剖面的拱度，当代各国（包括美、欧、俄）多采用NACAa=0.8为基础的形式。要求剖面叶背（吸力面）压降值，由导边到80%弦长处的压降相等；在随后的20%弦长内，压降系数降到随边为零。这导致剖面的流体合力作用中心有向导边移动的趋势，通常在距剖面弦向中点往导边0.10～0.25弦长处。由于桨叶侧斜后，外半径（r＞0.6）相对更加给力的剖面整体向随边移动，可以预期剖面合力作用中心也有相应移动。

调距桨转叶轴位置的选择，既要考虑设计工况船舶航行的需要，又要考虑船舶机动调距后的情况。下面提供一些经过实船运行考验的调距桨转叶轴相对位置数据，表1中的桨都经过装船后长期运行于不同螺距位置的情况，列出的是设计工况所对应的值。绕转叶轴转动（调距）后，有关数据将发生变化，包括桨的侧斜度。

表1 若干调距桨转叶轴位置相关数据

对若干调距桨的侧斜角θsk～数据进行分析比较，列出具有代表性的五型调距桨的侧斜分布特点于表1。虽然图纸所注侧斜度（projectedskewangle）不完全相同，但侧斜角θsk沿桨径向分布规律极其接近，即在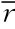 T≈0.78处，侧斜角θsk回到零，在桨毂处=hub，θsk=0起，慢慢向导边侧斜，在接近叶梢＞0.78处，剖面迅速向随边侧斜。其关系可用抛物线表示，即用式（2.1）表示。只要给定桨叶侧斜度θsk TOT，即

θsk=A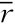（-hub）（-0.78） 　（2.1）

就可以确定具体桨的式（2.1）中的A值。的确，在dθsk/d=0处，侧斜角达到极值，即往导边侧斜最甚位置，侧斜角θsk出现拐点。由式（2.1）知：

由dθsk/d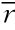=0，[2-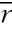（hub+0.78）]A=0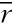，=（hub+0.78）/2=guai，该处的侧斜角为：

桨叶梢r=1.0处，侧斜角为：

桨叶的侧斜度为：θsk TOT=θsk Tip-θskguai=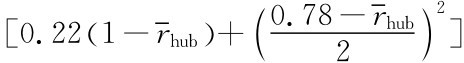A 　（2.2）

从式（2.2）中，已知rhub及θsk TOT值，可得出A值，随后得出该桨的侧斜θsk分布解析表达式，即

按上述解析关系算得之θsk～与工程图纸给定的数据绘算所得之θsk～的差异，逐点比较，均在±0.2°之间。在选定表1中直径D=1.85m、侧斜度25°的四叶调距桨时，采用该表中D=4.2m桨的侧斜分布θsk～，将侧斜角值按25°/40°比例缩小，与按式（2.1）算得的侧斜分布，相对角度差小于±0.2°。必须指出，虽然该两型桨的螺距比及叶数等均不同，实桨调试和运行中，并未出现与转叶力矩有关的问题。两型桨在调节到名义螺距比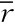（=0.7剖面转动后的相应值）约P/D≿1.5时，转叶机构仪表显示，桨转叶力矩由原来的负值转到了正值，即需要“拉”住曲柄销，以免桨叶自动转到更大螺距角位置。表1中所有桨的转叶轴（桨叶参考线）都是将桨叶面积基本平分，桨叶导边部分面积略大于随边部分的面积，占总面积的50%强。

有技术资料显示，俄罗斯（苏联）曾进行不同侧斜方式（常规轻微侧斜、大侧斜、径向呈S形中侧斜、先向导边后在外半径向随边侧斜—常规侧斜）桨叶的转叶力矩模型测试。与表1中所列各桨转叶轴的相对位置相比，桨叶导边部分面积只占总面积的40%左右，资料中的CM为负值，即转叶力矩有令桨叶往减小螺距角方向转动的趋势，CM的绝对值在0.005左右。数据还显示，大侧斜导致CM绝对值增大，即转叶力矩值波动更大。资料中未见桨螺距比数据，也未查到采用该类转叶轴位置的调距桨样机。

综上所述，为保证调距桨的顺利运行，正确选定转叶轴的位置，即照顾到以各种螺距运行时，桨叶合力作用中心与转叶轴的相对方位，并控制转叶力矩，非常重要。尤其是当代叶梢卸载侧斜螺旋桨，要确定桨叶合力作用中心，无论通过理论计算，还是模型试验，都非易事。特别是当桨叶绕转叶轴转动后，部分剖面进入分离绕流，部分剖面压力面和吸入面位置互换后，计算的物理模型基础和试验的模拟参数都有待商榷。因此，根据先前的工程实践经验，探索前行，至关重要。根据本节讨论，希望达到以下共识：高速航行时，应设法降低桨的扭矩Q及与之呼应的转叶力矩Mb，即降低转数（航速）后，再启动调距操作程序，在船舶应急状态（如紧急倒车、回转）也应同步降低桨转数，顾及桨的流体动力状态，再进行调距操作。

关于如何具体为新设计桨选定转叶轴位置问题，建议以有成功实用经验的调距桨为母型，来选定转叶轴位置。参照D=4.2m、θsk=40°、CT≈0.48五叶调距桨的经验数据，曾选定D=1.85m，θsk=25°，CT≈1.05四叶调距桨的转叶轴位置，顺利地满足了技术任务书要求，达到了预期工程效果。应该可以在此基础上继续践行。

3 绕转叶轴旋转时桨叶的转动惯量及附连水转动惯量

调距桨叶有绕转叶轴转动调节螺距的技术使命，由桨叶与桨毂相对静止到转动，必须改变原来的平衡，施加相应的力（矩）及相应的加速度，为此需要了解桨叶在所述运动时的转动惯量及附连水转动惯量，才能确定与相应加速运动有关的转叶力矩。

国际市场上有调距桨毂（包括转叶机构）的系列专利产品，却不包括桨的流体动力性能保证，这是因为，要根据特定的具体船—机—桨匹配需要，专门进行涉及螺旋桨推进、空泡、振动、噪声性能的流体动力设计。对于调距桨，还要加上改变螺距状态后的桨叶转叶力矩、绕流空泡化等问题的权衡。目前在研讨桨叶转叶力矩时，都默认了准定常假定，即认为转叶过程中，每一瞬间的作用力仅与该瞬间的速度有关，而与加速度无关。在专门的可调螺距螺旋桨论著中，有“与加速度有关的转叶力矩，其数值可忽略不计”的说法。由于没有找到提出这一观点的技术文献及论证依据，在下面将针对实际运行的调距桨案例来检查，证实关于“船用调距桨的调距过程中的加速度对转叶力矩的影响，可忽略不计”的论断。

3.1 桨叶绕转叶轴的转动惯量

图2所示为叶剖面沿转叶轴方向所见图形，铺在圆柱面上的厚度t的小段tdx到转叶轴的直线距离，小于该tdx段在圆柱面上到转叶轴的距离。因此，小段tdx绕转叶轴的转动惯量值t·dx×（距离）2小于t·dx·x2，认为剖面绕转叶轴的转动惯量为

图2 沿转叶轴向剖面视图

是高估剖面绕转叶轴的转动惯量，亦即高估与加速度有关的转叶力矩。按图2所注标记，C为剖面长（叶宽），由转叶轴到导边为CL，到随边为CT；t0为剖面厚，t为剖面当地局部厚，可将式（3.1）写成

由此可见，除与材料密度成正比外，剖面绕转叶轴的转动惯量与叶宽C成立方关系，与厚度成正比。式（3.2）中的积分值与剖面沿弦向的厚度分布有关，对于船舶螺旋桨常用的翼型剖面，相对厚度t/t0沿弦向相对位置的分布规律不变。故对于特定翼型剖面的积分值有

倘若以选作算例的表1中D=1.85m桨为例，采用的是NACA66厚度分布，计算其相对剖面中点的转动惯量值，即转叶轴与剖面中点重合的情况，有

表2 NACA66剖面转动惯量计算表

并由表2得

im0=ρmC3t0×402.5×10-3×0.1=0.04ρmC3t0 　（3.3）

若转叶轴偏离剖面中点，将导致转动惯量增大，其数值为剖面质量乘以偏移距离“l”的平方。通常转叶轴不会移出剖面宽度范围，即l＜。则剖面转动惯量增加Δim值，计及剖面面积，有

CS=S/Ct0=∑，表2中算得CS=0.718，桨叶导沿、随沿加厚后CS≥0.720。通过以上估算，可以估定侧斜桨叶剖面对转叶轴的惯量值在以下范围：

im=im0+Δim

im≈kρmC3t0，0.04＜k＜（0.04+0.18）=0.22 　（3.5）

整片桨叶相对转叶轴的转动惯量Im=imdr为由桨毂径rh到叶梢D/2的im积分。计及，可得Im表达式：

已知C/D、t0/D后，取k=0.04，由式（3.6）所得为桨叶绕转叶轴的最低转动惯量；取k=0.22，为桨叶可能高的转动惯量。仍以表1中D=1.85m桨叶为例，计算列于表3。表中还包括有计算桨叶质量的项，即Wm=

从而得到计算桨叶的质量：Wm=ρm×39.33×10-3×0.1=93.4kg及其绕转叶轴的转动惯量范围。

表3 D=1.85m桨叶惯性量计算

即实桨叶的转动惯量：13.8kg·m2＞Im＞2.5kg·m2。

3.2 桨叶绕转叶轴的附连水转动惯量

桨叶剖面通常是细长体形。按惯例，在研究、计算其绕图2中转叶轴转动时，将剖面看成平板，宽度为C，该剖面绕转叶轴的附连转动惯量为

式中，ρw——水密度，CL——转叶轴到导边的距离。当转叶轴取在剖面宽中点，即CL/C=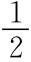，λw有最小值为λw=；当转叶轴取在导沿（或随沿）CL/C=0（或CL/C=1），λw有最高值为λw=ρw。即由于转叶轴相对桨叶剖面弦向位置不同，其附连水转动惯量λw的变化范围为

桨叶由桨毂rh到桨叶梢（D/2）整片桨叶的附连水转动惯量为

倘若所有剖面均取kw=1，得Im值最小；取kw=9，得Im值最大。综上所述，桨叶的附连水转动惯量值的变化范围如下：

对于材质密度ρm的桨叶绕转叶轴转动惯量Im及其附连水转动惯量的数值，可按式（3.6）、式（3.8）进行比较。对于侧斜桨叶，各半径处剖面的k及kw值为相对半径r的函数，加上C/D及t0/D均随r变化，故只能针对具体的桨叶进行估算，对一些具体工程用桨的计算显示，桨叶在空气中的转动惯量（Im）与在水中的转动惯量（Im+Iw）之比，大致在1∶3到1∶4之间。

关于D=1.85m算例桨，表3中列有其（C/D）4项及∑（C）D4的数值。若设定所有剖面的转动惯量λ中的系数kw=1.0，得桨叶的附连水转动惯量下限值：

假定kw=9.0，得到桨叶附连水转动惯量的可能上限值：

3.3 调距桨转叶过程中的角加速度

非定常运动物体的受力（矩），与运动体的惯性有关外，还与加速度值有关。当代调距桨的桨叶转动幅角，即由最大正螺距角到极限负螺距角的调节值，大致在60°左右，即π/3。转叶机构从全速前进螺距调至全倒退螺距，费时是15～30s（民船），军船用桨的时间接近15s。假如是周期性调节，即由原运行螺距回调到最低螺距，再往高调到最高螺距后，恢复到原运行螺距，费时为一个周期T，则有T为10～60s。

接到转叶指令后，转叶力矩的平衡被破坏，即在t瞬间，转叶加速度为，转动角速度ω=0。螺距角γ按下列关系变化：γ=Acos2πt/T+B，在t=0时，γ=γ0；t=T/2时，γ=γ1，则可得关系式：

在螺距调控期间可能出现的角速度和角加速度幅值为

式（3.9）中γ0-γ1为最大正螺距角与极限负螺距角之差，约为γ0-γ1==60°。为估计实际桨叶调距转动时的角速及加速值，表4中计算不同调控周期T所对应的数值，并以实桨D=1.85m为例，计及桨叶转动惯量Im，附连水转动惯量Iw及桨叶宽C等数值，可得出与加速有关的转叶力矩等的数据。表中列出的最高角速是反复调节螺距时可能达到的数值，高于平均角速度，除定性反映转叶曲柄机构运动的非线性特点外，可充分估计转叶机构调距时，桨叶剖面因之出现的线速度大小及其对桨叶绕流的影响。以D=1.85m算例桨为例，该桨=0.7处实际叶宽C=×D=0.468×1.85≈0.87m，若转叶轴通过剖面端点，则因调距导致的另一端的线速度为0.05～0.30m/s（见表4）之间。对于正绕桨轴以线速度u=30～50m/s旋转的桨叶剖面，由于调距引起的局部线速度与桨正常运行线速度相比较为（0.05～0.30）与（30～50）m/s之比，即由调距引起桨叶剖面局部绕流速度的变化，为千分之几，显然低于船后伴流场引起的剖面绕流速变化。这就是调距时只考虑螺距方位角变化，而不考虑绕流速度变化的理由。

表4 桨叶调距时可能的运动和受力估算

在3.1、3.2节中，曾算得D=1.85m桨桨叶的转动惯量在2.5～13.8kg·m2之间，而其在水中的附连转动惯量在4.37～39.33kg·m2之间。因此，桨叶的水中转动惯量最大可能值为ITOT=13.8+39.3≈53.1kg·m2。当最高可能角加速度|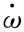|时（见表4），可出现瞬间转叶力矩峰值ΔMbmax=ITOT×||2≤53.1×|ω·|2max=53.1×0.2072≈2.3N·m。与“1”节中估算得到：342r/min时，Mb≈7.3k N·m=7300N·m；255r/min时，Mb≈3200N·m相比，由加速度引起的转叶力矩ΔMb比定常状态的转叶力矩Mb小3个量级。

前面“2”节中曾提到，苏、俄曾进行不同侧斜方式桨叶的转叶力矩模型试验，测得转叶力矩系数|CM|≈0.005～0.010区间。按其估算D=1.85m、P/D=1.400、Z=4叶调距桨每叶的定常转叶力矩：桨转数342r/min时，Mb=CMρn2D5≈（3610～7220）N·m；桨转数255r/min时，Mb≈（2010～4010）N·m之间，与“1”节中估算的最大转叶力矩值相当。

4 结论

调距桨的转叶力矩，是调距桨设计必须考虑的一个流体动力问题。与桨运转时的轴扭矩相比，转叶力矩数值可观，且随桨运行转数增高而变化，转叶力矩的方向会变化，数值会增大。因此，调控螺距时，必须适当限制转叶机构的启用条件，即规定在一定转数和航速条件下，才能进行调距。

对于侧斜式调距桨，转叶力矩的变化更为复杂，要考虑桨叶侧斜、纵倾的分布与桨叶力矩的关系，恰当选择转叶轴的相对位置，可以根据实桨的统计数据选择。

转叶机构操控时，会出现加速度，计及桨叶调节螺距角实际情况，所产生的转叶力矩变化，数值有限，工程上可以忽略不计。