基尔霍夫电流定律详解

电路按结构可分为分支电路和无分支电路。若分支电路可以通过串、并联方法简化为无分支电路，再应用欧姆定律便可得出计算结果。这类电路称为简单电路。凡不能用串、并联方法简化的分支电路称为复杂电路。复杂电路不能直接由欧姆定律求解。基尔霍夫于1845年创立了两条定律，称为分析电路的基本定律。

下面以如图1.4.1所示电路为例，先介绍电路的几个名词。

支路：流经同一电流的电路分支称为支路。在图1.4.1中，共有三条支路，即支路数b＝3。

节点：三条或三条以上支路的连接点称为节点。图1.4.1所示电路只有两个节点b和e，即节点数n＝2。其余各点a、c、d、f均不是节点。

图1.4.1　基尔霍夫定律例图

回路：电路中任一闭合路径称为回路。图1.4.1中有三个回路，它们是abef、bcde和acdf，即回路数l＝3。

网孔：未被其他支路分割的回路称为网孔。图1.4.1中有两个网孔，分别是abef和bcde。

1.4.1　基尔霍夫第一定律

基尔霍夫第一定律（KCL）又称为节点电流定律。该定律的内容是：对电路中任意一个节点，流入（或流出）该节点的电流的代数和恒等于零，即

节点的电流有流入和流出之分，分析时，设流入节点的电流为正，则流出节点的电流为负；反之亦然。图1.4.1中的节点b的电流代数和为

或改写成

式（1.4.1）表明，流入节点的电流总和恒等于流出节点的电流总和。

在利用该定律列方程前，必须标明支路电流的参考方向。电流参考方向的设定是任意的，当计算结果为正时，说明所设的参考方向与电流的实际方向相同；否则相反。

第一定律可以引申应用到广义节点上，所谓广义节点是指性质可以等效成节点的闭合面所包围的部分电路。例如，在图1.4.2（a）、（b）中，点画线框内分别为三角形连接负载和晶体三极管等效电路，它们都是广义节点。根据图示参考方向，对于图（a），有

对于图（b），有

图1.4.2　广义节点

1.4.2　基尔霍夫第二定律

基尔霍夫第二定律（KVL）又称回路电压定律。该定律的内容是：对电路任一闭合回路，电动势的代数和恒等于电压降的代数和，即

如果电动势也用其电压表示，则式（1.4.2）可改写为

式（1.4.3）表明，任一闭合回路内，沿回路一周各部分电压降的代数和恒等于零。

由于是电压降（或电动势）的代数和，在列回路电压方程时，必须规定回路的参考方向，或称绕行方向。以该绕行方向作为判断电压（或电动势）正、负号的标准，当电压（或电动势）的参考方向与绕行方向一致时，取正号；否则，取负号。例如，在图1.4.1中，根据绕行方向可列出两个回路电压方程式，即

E1－E2＝I1R1－I2R2

E2＝I2R2＋I3R3

同样地，基尔霍夫第二定律不只适用于具体回路，也可引申用来分析假想回路。例如，在图1.4.3中，ABCA可视为假想回路，因为A、B之间无实际支路，按图示绕行方向可写出电压方程式为

E2＝UAB＋IR2

同理　　－E1＝－UAB＋IR1

基尔霍夫定律是电路的基本定律，是分析和计算各种电路的基础。

图1.4.3　假想回路

【例1.4.1】　求如图1.4.4所示的各电路中的电流。图中，E＝10V，R＝2Ω，U＝4V，且它们的参考方向及回路绕行方向如图所示。

图1.4.4　例1.4.1的图

【解】　应用基尔霍夫回路电压定律求解如下：

图（a）　　－E＝IR－U

图（b）　　E＝IR－U

图（c）　　－E＝－IR－U

图（d）　　E＝－IR－U

本例所导出的计算电流I的四个表达式是物理学中的全电路的欧姆定律，或称含源电路的欧姆定律。

思考与练习

1.4.1　在如图1.4.5所示电路中，有几个节点？几条支路？几个网孔？几个回路？请列出各节点的KCL方程和网孔的KVL方程。

1.4.2　求如图1.4.6所示电路中电流I3的值，已知I1＝2A，I2＝－3A，I4＝1A，I5＝－2A。

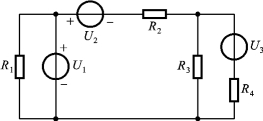
图1.4.5　题1.4.1的图

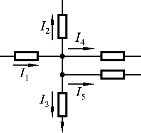
图1.4.6　题1.4.2的图

1.4.3　在如图1.4.7所示电路中，若I1＝5A，求I2；若AB支路断开，求I2。

1.4.4　试应用基尔霍夫电压定律写出如图1.4.8所示各支路中电压与电流的关系式。

图1.4.7　题1.4.3的图

图1.4.8　题1.4.4的图