戴维宁定理与诺顿定理

在有些情况下，只需要计算一个复杂电路中某一支路上的电压或电流，这时用前面介绍的分析方法必然会引出一些不必要的电压、电流，为了尽量简化分析，常常应用等效电源的方法。

什么是等效电源呢？如图2.7.1（a）所示电路，如果只需要研究其中RL支路的电流（或电压）时，可将RL支路单独划出来，而把其余部分（图中虚线框内）看成一个有源二端网络，因此图2.7.1（a）可画成图（b）的形式。所谓二端网络，就是具有两个出线端的部分电路，按其内部是否含有独立电源，分为有源二端网络NS和无源二端网络NO。习惯将要研究的部分（如图中的RL支路）称为外电路。

有源二端网络内部可以是简单的或是任意复杂的电路，不论其内部结构如何，对外电路而言，它仅仅是起一个电源的作用，它对外电路供给了电能。因此，这个有源二端网络可以变换成一个等效电源。前面讲过，电源模型有两种，一种是电压源与电阻串联的模型，一种是电流源与电阻并联的模型。由两种等效电源模型得出戴维宁定理与诺顿定理。

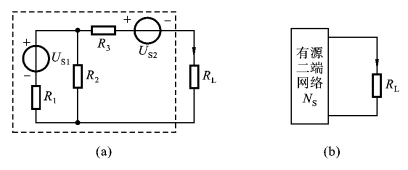
图2.7.1　有源二端网络

2.7.1　戴维宁定理

戴维宁定理：任何一个线性有源二端网络，对于外电路而言，都可以用一个理想电压源和内阻串联的电路模型来代替，如图2.7.2所示，理想电压源的电压就是有源二端网络的开路电压UOC，即将负载断开后，a、b两端之间的电压，内阻R0等于有源二端网络化为无源二端网络（电压源短路、电流源开路）后a、b两端的等效电阻。

图2.7.2　戴维宁定理

下面对戴维宁定理给出一般证明。

如图2.7.3（a）所示电路中，a、b两端的左边是一线性有源二端网络NS，右边是外部电路RL。设a、b两端电压为U，电流为I。首先，将外部电路RL用一个理想电流源代替，其大小和方向与I相同，如图2.7.3（b）所示，根据等效的概念，这样的替代并不影响Ns内部的电压和电流。

其次，应用叠加定理将图2.7.3（b）中U、I看成是图2.7.3（c）中U′、I′和图2.7.3（d）中U″、I″的叠加。

图2.7.3（c）是有源二端网络内部的独立电源单独作用时的情况，此时，外部电流源不作用，即有源二端网络处于开路状态。若令有源二端网络开路电压为UOC，这时有I′＝0，U′＝UOC。图2.7.3（d）是外部电流源单独作用时的情况，此时有源二端网络内部的独立电源不作用，也就是把有源二端网络化为一个无源网络，对外部而言，它可用等效电阻R0替代。这时有I″＝I，U″＝－IR0。

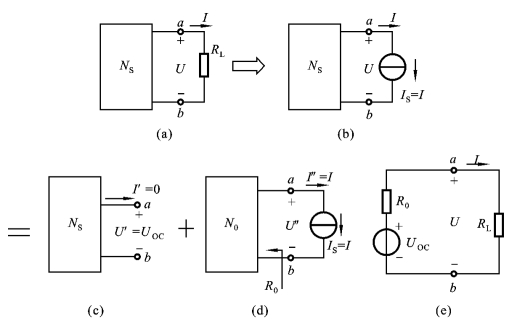
图2.7.3　戴维宁定理的证明

将图（c）和图（d）叠加，得

由式（2.7.1）得出的等效电路正好是一个电压源UOC与电阻R0串联的电路，如图（e）所示。也就是说，图（e）和图（a）对外部电路而言是等效的，在RL支路中产生相同的电流和电压。

戴维宁定理是阐明线性有源二端网络外部性能的一个重要定理，若只需计算某一支路的电流或电压，则应用戴维宁定理具有特殊的优越性。应用戴维宁定理求解电路的过程如下。

（1）将待求支路从原电路中移开，求余下的有源二端网络NS的开路电压UOC；

（2）将有源二端网络的所有电压源短路，电流源开路，求出无源二端网络的等效电阻R0；

（3）画出UOC和R0串联的戴维宁等效电路，再将待求支路接入，求相关的电压或电流。

需要注意的是，戴维宁定理只适用于线性电路，不适用于非线性电路。

【例2.7.1】　用戴维宁定理求图2.7.4（a）所示电路中流过R2的电流I2。

【解】　（1）根据戴维宁定理，将待求支路R2移开，形成有源二端网络，如图（b）所示，可求开路电压。

UOC＝Uac＋Udb＝［4×2－（1×3＋12）］V＝－7V

（2）将有源网络化为无源网络，如图（c）所示。R0＝7Ω。

（3）作出戴维宁等效电路并与待求支路相连，如图（d）所示。

图2.7.4　例2.7.1的图

【例2.7.2】　用戴维宁定理求图2.7.5（a）电路中I、U。

【解】　根据戴维宁定理，先将R支路移开，其余部分所构成的二端网络如图2.7.5（b）所示。

（1）用节点电位法可求得

图2.7.5　例2.7.2的图

（2）将有源网络化为无源网络，将两个独立电源变为零值，2V电压源短路，1A电流源开路，如图2.7.5（c）所示。

（3）根据所求得的UOC和R0，可作出戴维宁等效电路，并与R支路相连，如图2.7.5（d）所示，可求得

2.7.2　诺顿定理

诺顿定理：任何一个线性有源二端网络，对于外电路而言，都可以用一个理想电流源和内阻并联的电路模型来代替，如图2.7.6（a）、（b）所示，理想电流源的电流就是有源二端网络的短路电流ISC，即将负载短路后a、b之间的电流，内阻R0等于有源二端网络化为无源网络（电压源短路、电流源开路）后a、b两端的等效电阻。

图2.7.6　诺顿定理的图解说明

图2.7.6中，图（b）就是图（a）的诺顿等效电路，ISC、R0可通过图（c）、（d）求得。在前面曾经学习过，两种电源模型是可以等效变换的，显然，对于一个线性有源二端网络来说，其诺顿等效电路与戴维宁等效电路本质上是相同的。

【例2.7.3】　如图2.7.7（a）所示电路，已知电阻R1＝R2＝2Ω，R3＝6Ω，电压源US2＝8V，电流源IS1＝4A，用诺顿定理求I。

图2.7.7　例2.7.3的图

【解】　根据诺顿定理，将R3支路移开，其余部分所构成的二端网络用一个电流源ISC和电阻R0并联的电路等效，先求短路电流ISC，如图（b）所示。根据叠加定理，ISC等于8V电压源、4A电流源分别作用时的短路电流的代数和。

将有源网络化为无源网络，将两个独立电源变为零值，8V电压源短路、2A电流源开路，如图2.7.7（c）所示。

R0＝R2＝2Ω

根据所求得的ISC和R0，可作出诺顿等效电路，并与R3支路相连，如图2.7.8（d）所示，可求得

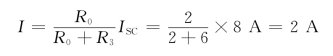
2.7.3　最大功率传输定理

给定一线性有源二端网络，如接在它两端的负载电阻不同，则从二端网络传输给负载的功率也不同。在电子技术中，常常希望负载能够获得最大功率，例如，希望一台扩音机所接的喇叭放出的声音最大。在什么情况下，负载才能获得最大功率呢？

图2.7.8（a）表示线性有源二端网络NS向负载RL传输功率，图2.7.8（b）是其戴维宁等效电路接入负载的情况。

图2.7.8　最大功率传输定理

由图2.7.8（b）可知，负载上的电流

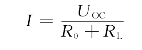
负载获得的功率

由此可见，P是关于RL的函数，要使P最大，必有，而

因此，当RL＝R0时P取得最大值，即

线性有源二端网络NS向负载RL传输功率，当RL＝R0时负载获得最大功率，这就是最大功率传输定理。电路的这种工作状态称为负载与电源“匹配”。显然，匹配时有一半的功率消耗在电源内部，电路传输的效率仅为50%。在电信工程中，由于信号一般很弱，常要求从信号源获得最大功率，因而必须满足匹配条件，传输效率属次要问题；而在电力系统中，输送功率很大，效率非常重要，故应使电源内阻（以及输电线路电阻）远小于负载电阻。

思考与练习

2.7.1　如图2.7.9所示电路，分别求出其戴维宁等效电路和诺顿等效电路。

2.7.2　测得一有源二端网络的开路电压为10V，短路电流为2A，试画出其戴维宁等效电路和诺顿等效电路。

2.7.3　分别应用戴维宁定理和诺顿定理计算如图2.7.10所示电路中4Ω电阻上的电流。

图2.7.9　题2.7.1的图

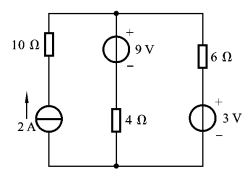
图2.7.10　题2.7.3的图