8.3.1 系统误差、随机误差和疏失误差
如果从不同的角度出发，误差的分类方法较多。前面讨论的绝对误差、相对误差的概念是按误差的表示方式分类的。若按误差出现的规律（或误差产生的原因及误差的性质）分类，误差又可以分为系统误差、随机误差和疏失误差。
1.系统误差
如果测量过程中产生的一些误差的大小和正负是恒定不变的，或在条件变化时遵循一定的规律变化，这种误差称为系统误差，又称为确定性误差。例如，若用零点不准确的万用表对电量进行多次测量，其误差基本上是恒定的，属于系统误差。
产生系统误差的原因包括：测量仪器不准确、有缺陷或放置不当；温度变化、电源电压波动等外界环境发生变化；测量人员有偏视等读数习惯及近似计算等。
系统误差是测量中的主要误差，测量的准确度是由系统误差表征的，系统误差越小，测量结果的准确度越高。
系统误差用字母ε表示，它的计算方法是
式中：xav等于对同一量多次测量数据的算术平均值，即
式中：n为测量次数。式（8.3.1）中的x0是被测量的实际值，它可以用准确度较高的仪器的测量值来代替。
【例8.3.1】 有一组电流的测量数据如表8.3.1所示，其测量次数为11次。求系统误差。
表8.3.1 数据表
【解】 测量数据的算术平均值为
设其实际值为I0＝5.21A，则所求系统误差为
减小系统误差的方法主要是采取必要的技术措施。例如，使用前对仪表进行校正；提高仪表的准确度；减小视差；改善环境条件等。
2.随机误差
在同一条件下，对同一量进行多次测量，其误差的大小及正负规律不可预知，即或大或小、或正或负，这种误差称为随机误差，又称不确定误差。例如，在同一条件下，用万用表每隔一定时间去测量同一电量，每次测得的数据不完全相同，但相差不大，这种误差便是随机误差。
产生随机误差的原因包括：噪声、电磁场的干扰、电源电压突变等周围环境因素的影响。
从理论上讲，当测量次数趋于无穷大时，随机误差的算术平均值趋近于零。因此，减小随机误差的方法是对同一量进行多次测量，然后取其平均值，使正负误差相互抵消。
当能设法基本消除系统误差时，随机误差为每次测量值与实际值之差，即
若测量次数足够多，将由各次测量值所求出的δi值平方后求和，再求出它的算术平均值，该数值称为方差，即
式中：取平方是为了使负误差平方后变为正值，使正负方向的误差不能相互抵消，因而它可用来反映测量值的分散程度。方差越小，表示测量值越集中。
将方差开方，取其正方根，称为标准差，即
若测量次数为有限值，便可用贝塞尔公式计算标准差，该式为
式中：算术平均值xav代替了式（8.3.3）中的x0，使计算变得更加方便；xi为各次测量值。
【例8.3.2】 由表8.3.1中的数据，求标准差。
【解】 先求出每次测得的电流值Ii与电流平均值Iav之差，然后平方相加，结果为0.803 A，代入式（8.3.5），得标准差为
3.疏失误差
由于读数、记录、计算或操作上的错误，造成在一定条件下的测量值明显偏离实际值。这样形成的误差称为疏失误差。
疏失误差应当尽量避免。经判断的确存在疏失误差时，应将该数据从测量数据中剔除。如果是作精密测量，当对测量所列数据进行处理时，对于测量值与算术平均值之差大于3σ的那次数据，应当作为疏失误差处理。这种含有疏失误差的数据称为可疑数据或异常数据。
8.3.2 测量数据的处理
1.可疑数据的剔除
最大的绝对误差，也称为误差极限。对可疑数据的取舍准则是Δxm＝3σ。即当某次测量值与算术平均值之差大于3σ时，就可以认为该数据可疑，可予以剔除。
【例8.3.3】 判断表8.3.1所示的数据中有无可疑数据。
【解】 误差极限Δxm＝3σ＝3×0.28A＝0.84A
表8.3.1所示的测量数据中，所有Ii－Iav的值均小于0.84A，所以无可疑数据，不需剔除。
如果有可疑数据需要剔除时，也必须持慎重态度。因为它可能反映出一种尚未发现的物理现象。
2.有效数字与数字的舍入规则
由于测量数据不可避免地存在误差，而且对测量数据进行运算时还常有π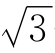
等无理数需要取近似值，因此会造成计算值的不精确。
有效数字的位数应该由测量的准确度决定，而且与误差大小相适应。当用一个数表示一个量时，如果绝对误差不超过末位单位数字的一半，则从第一个非零数字算起，到最末一位数字（包括零）为止，都称为有效数字。例如，12.5A的末位是十分位，一般规定其绝对误差范围为±0.05A。显然，数据的末位是欠准数字，末位以前的数字是准确数字，数字的位数不是越多越好，一般只允许最末一位是欠准数字。
在测量数据较多的情况下，数字的舍入规则为：设有效数字的末位为第m位，当第m位为奇数时，其后位的“5”入；第m位为偶数时，其后位的“5”舍。这种舍入法的好处有两点：①最后一位数字为偶数，运算时除尽机会多，可减少计算机上的误差；②可以抵消多次舍入引起的误差，因为第m位取偶数和取奇数机会均等，则最末位入1和不入1的机会也均等。以23.45和17.15为例，如果保留三位有效数字，它们应分别写为23.4和17.2，而不是23.5和17.2。这种方法，称为“偶数法则”即“5以下舍，5以上入”、“5前奇入、5前偶舍”。
【例8.3.4】 用一只0.5级10A的电流表测量电流，其指示值为8.84A，试确定有效数字的位数。
【解】 该表的最大绝对误差为
由此可知，测量值的十分位是有效数字的末位，则此数据的有效数字该取两位，对8.84用舍入规则处理，其测量结果应为8.8A。
思考与练习
8.3.1 按误差出现的规律，误差可以分为哪几类？
8.3.2 对于测量数据，处理方法是什么？
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
