半导体物理基础

按照电阻率的不同，可以将材料分为三类：导体（如银、铜、铝、铁等）、绝缘体（如塑料、陶瓷、橡皮、石英玻璃等）和半导体（如硅、锗等）。三者之间虽然在电阻率的区分上无绝对明确的界限，但在性质上却有很大差别。由于半导体具有许多特殊的性质，因而在电子工业与光电工业等领域占有极其重要的地位，例如，大部分光辐射探测器都是采用半导体材料制成的。

半导体材料大多数是晶体材料。晶体可分为单晶体和多晶体。在一块材料中原子全部有规则地呈周期性排列，这种晶体称为单晶体。如果只在很小范围内原子有规则地排列，形成小晶粒，而晶粒之间还有无规则排列的晶粒界，这种材料称为多晶体。

1.2.1 能带理论基础

为了解释固体材料的不同导电特性，人们从电子能级的角度引入了能带理论，它是半导体物理的理论基础。应用能带理论可以解释发生在半导体中的各种物理现象和各种半导体器件的工作原理。

1.电子的共有化运动

物质是由原子组成的。原子以一定的周期重复排列所构成的物体称为晶体。在晶体中，电子的运动状态与孤立原子中的电子状态有所不同。在孤立原子中，原子核外的电子按照一定的壳层排列，每一壳层容纳一定数量的电子。电子在壳层上的分布遵守泡利不相容原理和能量最低原理，并具有确定的分立能量值，也就是电子按能级分布。

当原子结合成晶体时，由于原子之间的距离很近，不同原子之间的电子轨道（量子态）将发生不同程度的交叠，而晶体中两个相邻原子的最外层电子的轨道重叠最多。这些轨道的交叠使电子可以从一个原子转移到另一个原子上去。结果，原来隶属于某一原子的电子，不再为此原子所私有，而是可以在整个晶体中运动，为整个晶体所共有，这种现象称为电子的共有化（见图1－2）。晶体中原子内层和外层电子的轨道交叠程度很不相同，越外层电子的交叠程度越大，且原子核对它的束缚越小。因此，只有最外层电子的共有化特征才是显著的。

电子共有化会使得本来处于同一能量状态的电子出现微小的能量差异。例如，组成晶体的N个原子在某一能级上的电子本来都具有相同的能量，现在它们由于处于共有化状态而具有各自不尽相同的能量，因为它们在晶体中不仅仅受本身原子势场的作用，而且还受周围其他原子势场的作用。如果一块晶体中具有N个原子，那么这N个原子中每一个相同能级都将分裂成为N个新的能级，这N个能级之间的能量差异极小。这一能量区域中密集的能级通常称为能带。一般N值很大，这N个能级就形成了有一定宽度的能带。图1－3为能带的示意图，能带是描述晶体中电子状态的重要方法。

图1－2 电子共有化运动示意

图1－3 原子能级分裂成能带示意

2.晶体中电子的能带

原子中每一电子所在能级在晶体中都分裂成能带。这些允许被电子占据的能带称为允带。允带之间的范围是不允许电子占据的，这一范围称为禁带。

如同在原子中一样，在晶体中电子的能量状态也遵守能量最低原理和泡利不相容原理。电子总是先占满内层能级所分裂的允带，然后再占据能量更高的外面一层允带。原子中最外层电子称为价电子。晶体最外层电子壳层分裂所形成的能带称为价带。价带可能被电子填满，也可能不被填满。被填满的能带称为满带。

根据泡利不相容原理，每个能级只能容纳自旋方向相反的两个电子，在外加电场上，这两个自旋相反的电子受力方向也相反，它们最多可以互换位置，不可能出现沿电场方向的净电流，所以满带电子不导电。同理，未被填满的价带就能导电。金属之所以有导电性就是因为其价带是不满的。

图1－4所示为绝缘体、半导体、导体的能带情况。一般情况下，绝缘体的禁带比较宽，价带被电子填满，而导带一般是空的。半导体的能带与绝缘体相似，在绝对零度时，也有被电子填满的价带和全空的导带，但其禁带比较窄。正因为如此，在一定的条件下，其价带的电子容易被激发到导带中去。半导体的许多重要特性就是由此引起的。而导体的能带情况有两种：一种是它的价带没有被电子填满，即最高能量的电子只能填充价带的下半部分，而上半部分空着；一种是它的价带与导带相重叠。

需要说明的是，以上关于能带形成的论述是十分粗糙且不严格的。能带和原子能级之间的对应关系，并不像图1－4所示那样单纯，也并不永远都是一个原子能级对应于一个能带。能带图并不实际存在，而只是用来说明电子的能量分布情况。

图1－4 绝缘体、半导体、导体的能带情况

3.本征半导体和非本征半导体

半导体中的导带电子和价带空穴可在体内自由运动，二者统称为载流子。按照半导体中载流子的激发机理不同，可以将半导体分为本征半导体和非本征半导体。

1）本征半导体

本征半导体是指没有杂质、没有缺陷的理想半导体，即设想半导体中不存在任何杂质原子，并且原子在空间的排列也遵循严格的周期性。

半导体材料中原子的化学结构多为共价键。例如，锗（Ge）或硅（Si）原子外层有4个价电子，它们与相邻原子组成共价键后形成原子外层有8个电子的稳定结构。在绝对零度时，半导体材料不导电。但是，共价键上电子所受束缚力较小，它会因为受到热激发而越过禁带，去占据禁带上面的能带。比价带能量更高的允带称为导带。从价带跃迁到导带后，在导带中的电子称为自由电子。它们能量很高，不附着于任何原子上，因此有可能在晶体中游动，在外加电场作用下形成电流。价带中的电子跃迁到导带后，价带中出现的空缺称为自由空穴。在外电场作用下，附近电子可以去填补空缺，相当于自由空穴发生定向移动形成自由空穴运动，从而形成电流。所以，在常温下半导体有导电性。

由上可知，与半导体导电特性有关的能带是导带和价带。本征半导体的能带结构如图1－5（a）所示。在本征半导体中，电子获取热能后从价带跃迁到导带，导带中出现自由电子，价带中出现自由空穴，出现电子－空穴对导电载流子。本征半导体导电性能高低与材料的禁带宽度有关。禁带宽度越小，电子越容易跃迁到导带，因而导电性就越高。

锗的禁带宽度比硅的小，所以其导电性随温度的变化就比硅更显著。绝缘体因禁带宽度很大而无导电性。

2）非本征半导体

在半导体中人为掺入少量杂质而形成的掺杂半导体，通常称为非本征半导体。杂质对半导体的导电性有很大的影响，非本征半导体的导电性能完全由掺杂情况决定。

如果在四价原子锗（Ge）组成的晶体中掺入五价原子砷（As），在晶格中某个锗原子被砷原子所替代。五价原子砷用4个价电子与周围的锗原子组成共价键，尚有1个电子多余，这个多余电子受原子的束缚力要比共价键上的电子所受束缚力小得多，它很容易被砷原子释放，跃迁到导带而形成自由电子。易释放电子的原子称为施主。施主束缚电子的能量状态称为施主能级，它位于禁带之中，比较靠近材料的导带底（能级能量用Ec表示）。施主能级能量Ed和导带底能级能量Ec之间的能量差为ΔEd，它称为施主电离能。这种由施主控制材料导电性的半导体称为N型半导体，其能带结构如图1－5（b）所示。在N型半导体中，自由电子浓度高于自由空穴浓度。

图1－5 半导体的能带结构

同理，如果在四价锗晶体中掺入三价原子硼（B），将形成P型半导体。晶体中某锗原子被硼原子所替代，硼原子的3个价电子和周围锗原子的4个价电子组成共价键，形成8个电子的稳定结构还缺1个电子，于是它很容易从锗晶体中获取1个电子形成稳定结构。这样就使硼变成负离子而在锗晶体中出现自由空穴。容易获取电子的原子称为受主。受主获取电子的能量状态称为受主能级。受主能级能量用Ea表示。如图1－5（c）所示，受主能级也处于禁带之中，比较靠近材料的价带顶（能级能量用Ev表示）附近。Ea和Ev之差ΔEa称为受主电离能。受主电离能愈小，价带中的电子愈容易跃迁到受主能级上去，在价带中的自由空穴浓度也愈高。在P型半导体中，自由空穴浓度高于自由电子浓度。

1.2.2 热平衡下的载流子

半导体的电学性质与材料的载流子浓度有关。所谓载流子浓度是指单位体积内的载流子数。在一定温度下，若没有其他的外界作用，半导体中的自由电子和空穴是由热激发产生的。电子从不断热振动的晶体中获得一定的能量，从价带跃迁到导带，形成自由电子，同时在价带中出现自由空穴。在热激发的同时，也有电子从导带跃迁到价带并向晶格放出能量，这就是电子－空穴对的复合。在一定温度下激发和复合两种过程形成平衡，称为热平衡，这时的载流子浓度即为某一稳定值。当温度改变后，原来的平衡状态就被破坏而建立起新的平衡状态，即达到另一个稳定值。由固体理论得知，热平衡时半导体中自由载流子浓度与两个参数有关：一是能带中能级的分布；二是在这些能级中每一个能级可能被电子占据的概率。

1.能级密度

能级密度是指在导带和价带内单位体积、单位能量的能级数目，用N（E）表示。由固体理论得知，在导带内的能级密度

在价带内的能级密度

式中：N（E）为在电子能量为E处的能级密度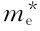；为自由电子的有效质量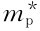；为自由空穴的有效质量；h为普朗克常量；Ec为导带底能量；Ev为价带顶能量。

由式（1－1）、式（1－2）可知，当离导带底或价带顶愈远时，能级密度N（E）愈大。

2.费密能级能量和电子占据率

关于电子占据能级的规律，根据量子理论和泡利不相容原理，半导体中电子的能级分布服从费密统计分布规律。在热平衡条件下，能量为E的能级被电子占据的概率为

式中：EF为费密能级能量；k为玻尔兹曼常数；T为热力学温度。

EF是热平衡条件下的一个重要参数。可以说，EF可决定电子在能级上的分布。实际上， EF等于把一个任意能量的电子加入热系统后所引起的系统自由能的改变。

当T＝0K时，由式（1－3）可以看出，若E＜EF，则fn（E）＝1。这说明：在绝对零度时，凡是能量比EF小的能级，被电子占据的概率均为1。也就是说，电子全部占据费密能级以下的能级，而费密能级以上的能级是空的，不被电子占据。

当T＞0K时，可以分为三种情况：

①若E＝EF，则fn（E）＝0.5，因此通常把电子占据率为0.5的能级定义为费密能级；

②若E＜EF，则fn（E）＞0.5，说明比费密能级能量低的能级被电子占据的概率大于0.5；

③若E＞EF，则fn（E）＜0.5，说明比费密能级能量高的能级被电子占据的概率小于0.5。

比费密能级能量高得愈多的能级，被电子占据的概率愈小。此外，电子占据高能级的概率还随温度的升高而增加。

在价带中，如已知电子的占据概率，即可求出空穴的占据概率fp（E）。空穴的占据概率也就是不被电子占据的概率，即

3.平衡载流子浓度

在导体中，能级能量为E的电子浓度等于在该能级处的能级密度和被电子占据概率的乘积。即

n（E）＝N（E）·fn（E）

在整个导带中总的电子浓度n应该是n（E）在导带底以上所有能量状态上的积分。即

将式（1－1）及式（1－3）代入上式，得积分结果为

式中：Nc为导带有效能级密度，Nc＝2。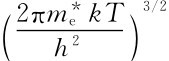

式（1－5）说明，自由电子浓度n与温度有关，在温度一定时n与EF呈指数关系。

同样，在价带中能级能量为E的能级处空穴浓度为

p（E）＝N（E）·fp（E）

整个价带中的空穴浓度p为

式中：Nv为价带有效能级密度，Nv＝2。

式（1－6）说明，价带中的自由空穴浓度p也是温度的函数，也与费密能级的位置有关。

把式（1－5）和式（1－6）相乘，可得

式中：Eg为禁带宽度，Eg＝Ec－Ev。由式（1－7）可得到如下结论：

①在半导体中，平衡载流子的电子数和空穴数的乘积与EF无关；

②禁带宽度Eg愈小，n和p的乘积愈大，半导体的导电性愈好；

③半导体中的载流子浓度随温度的增加而增大。

4.本征半导体中的载流子浓度

在本征半导体中，自由电子浓度等于自由空穴浓度。即

ni＝pi

由式（1－5）、式（1－6）得

于是，得到本征半导体的费密能级能量

式中：Ei为中间能级能量，中间能级处于禁带中间位置。对于硅、锗等半导体材料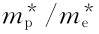，＝0.5～1；对于砷化镓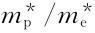，＝7.4。式（1－8）右侧的第二项很小，可以忽略。由此可知，本征半导体的费密能级位于禁带中线处，大体上与中间能级重叠。

由式（1－7）得到本征半导体载流子浓度为

5.掺杂半导体载流子浓度

N型半导体中，施主原子的多余价电子易跃迁进入导带，使导带中的自由电子浓度高于本征半导体的电子浓度。室温下施主原子基本上都电离，此时导带中的电子浓度

n＝Nd＋pi≈Nd 　（1－10）

式中：Nd为N型半导体中掺入的施主原子浓度。

空穴的浓度为

将式（1－5）代入式（1－10），得N型半导体的费密能级密度为

式中：ni为本征半导体载流子浓度。于是

由式（1－12）可知：N型半导体中的费密能级位于禁带中央以上；掺杂浓度愈高，费密能级离禁带中央愈远，愈靠近导带底。

同样，在P型半导体中，由于受主原子易从价带中获得电子，因此价带中的自由空穴浓度将高于本征半导体中的自由空穴浓度。设掺入的受主浓度为Na，那么室温下价带中的空穴浓度p和电子浓度n分别为

p＝Na＋n≈Na 　（1－13）

将式（1－6）代入式（1－13），得到P型半导体的费密能级能量

由式（1－15）可知：P型半导体的费密能级位于禁带中央位置以下；掺杂浓度愈高，费密能级离禁带中央愈远，愈靠近价带顶。

图1－6所示为本征半导体和掺杂半导体中的费密能级位置。

图1－6 半导体中的费密能级位置

1.2.3 非平衡载流子

大多数半导体器件通过外部注入载流子或用光激发方式而使载流子浓度超过热平衡时的浓度。这些超出部分的载流子通常称为非平衡载流子或过剩载流子。

1.材料的光吸收效应

物体受光照射时，一部分光被物体反射，一部分光被物体吸收，其余的光透过物体。那些被物体所吸收的光会改变物体的一些性能。

1）本征吸收

半导体材料可吸收光子能量并将其转换成电能，这是光电器件的工作基础。半导体材料吸收光的原因在于光与处在各种状态的电子、晶格原子和杂质原子的相互作用。其中最主要的光吸收是在光子的作用下，电子由价带跃迁到导带而引起的，这种吸收称为本征吸收，图1－7为本征吸收的能带示意图。电子从半导体价带跃迁到导带是一种本征激发，所以本征光吸收也就是本征激发所对应的光吸收。激发使得自由电子与空穴的浓度都有增加。由于价带顶和导带底之间存在一定的禁带宽度Eg，因此，只有当入射光子的能量大于该材料的禁带宽度时，即hν≥Eg时，才可能发生本征激发。因而，对某一半导体而言，本征吸收存在着一个相应于禁带宽度的长波限λ0。当光波长超过λ0，也就是频率更低时，就不能引起本征吸收。λ0的表达式为

式中：c为光在真空中的传播速度；h为普朗克常量；Eg为禁带宽度（eV）。

本征吸收是很强的吸收，其吸收系数可达105cm－1数量级。因此，实际的光吸收发生在材料表面约等于10－6cm的薄层内。这说明与光吸收有关的现象，往往要受到材料表面状态的影响。

2）杂质吸收

在光照下，掺有杂质的半导体内中性施主的束缚电子可以吸收光子而跃迁到导带。同样，中性受主的束缚空穴亦可以吸收光子而跃迁到价带。这种吸收称为杂质吸收，图1－8为杂质吸收的能带示意图。施主释放束缚的电子到导带，受主释放束缚空穴到价带，相应过程中所需能量称为电离能ΔEd（或ΔEa）。即杂质吸收光的长波限

或

图1－7 本征吸收能带示意

图1－8 杂质吸收能带示意

由于杂质的电离能ΔEd、ΔEa一般比禁带宽度Eg小得多，所以杂质吸收的光谱在本征吸收的长波限λ0以外。

3）其他吸收

其他形式的光吸收还有激子吸收、自由载流子吸收、晶格吸收等。这些吸收很大程度上是将能量转换成热能，从而增加了热激发载流子浓度。

引起光电导现象的主要是本征吸收和杂质吸收。

2.非平衡载流子浓度

半导体在热平衡状态下，其载流子的浓度有一个恒定的数值。这时，半导体内部由于热激发而不断地产生电子和空穴，同时，电子和空穴也不断相遇并消失，这称为电子和空穴的复合。当电子和空穴的产生率和复合率相等时，系统将保持相对平衡状态。但在外界因素的作用下，例如半导体接收光照，由于光的激发，电子和空穴的产生率大于复合率，这就可能在导带和价带增加载流子（电子和空穴）的数目。这种增加的电子和空穴称为非平衡载流子，增加的电子和空穴的浓度分别用Δn和Δp表示。这样，在导带和价带中电子和空穴的浓度分别为

n＝n0＋Δn 　（1－17）

p＝p0＋Δp 　（1－18）

式中：n0、p0分别表示光照前一定温度下热平衡载流子的浓度。

当半导体继续接收恒定光照时，电子和空穴的产生率保持在高水平，而复合率将随着非平衡载流子的增加而增大，直到复合率等于产生率，系统达到新的稳定状态为止，这时载流子浓度n与p保持不变。当光照停止时，产生率下降，系统的稳定状态遭到破坏，由于存在非平衡载流子，复合率超过产生率，载流子浓度减小。随着载流子浓度的减小，复合率也随之下降，直至复合率又等于产生率为止，载流子浓度保持光照前的数值n0和p0不变，系统恢复到平衡态。

1）描述复合的参数——寿命

非平衡载流子Δn（或Δp）的复合率一般可表示为

复合率＝Δn／τ（或Δp／τ） 　（1－19）

式中：τ为常数，称为非平衡载流子的寿命。τ的物理意义有如下三点。

①寿命τ的数值反映非平衡载流子复合的快慢。从式（1－19）可看出：寿命τ越长，复合率越小；寿命τ越短，复合率越大。

②τ就是非平衡载流子浓度衰减到原来的1／e所需的时间。在没有外界作用时，非平衡载流子浓度的变化率等于复合率（这里只考虑Δn，Δp也有同样的形式），即

dΔn／dt＝－Δn／τ 　（1－20）

式中：右边的负号表示复合作用使Δn随时间t减小。Δn是时间t的函数。从式（1－20）解得

Δn（t）＝Δn（0）e－t／τ 　（1－21）

式中：Δn（0）为t＝0时非平衡载流子的浓度。当t＝τ时，非平衡载流子浓度衰减到原来的1／e，即

Δn｜t＝τ＝Δn（0）e－t／τ｜t＝τ＝Δn（0）／e 　（1－22）

③τ是非平衡载流子的平均存在时间。非平衡载流子是逐步消失的，Δndt为所有非平衡载流子存在时间的总和，而非平衡载流子的总数就是t＝0时的载流子数目Δn（0）。所以，载流子平均存在的时间为

2）非平衡载流子的复合

非平衡载流子的复合大致可分为两种：直接复合和间接复合。

（1）直接复合 直接复合是指导带电子直接落在价带空穴的位置上，与空穴结合而失去其自由态的过程。通常，直接复合会辐射出光子来，这种光子的能量等于自由载流子复合时所放出的能量，其数值大致等于晶体禁带宽度。这种光辐射有时称为带边辐射。直接复合很重要，但是通常不在复合过程中起主要作用。

设n和p分别表示电子和空穴的浓度。每一个电子都有可能和空穴相遇而复合，它们的复合率和它们的浓度成正比。因此，单位体积内电子、空穴的复合率为

复合率＝γnp 　（1－24）

式中：γ称为复合系数或复合概率。

在热平衡的状态下，复合率等于产生率，则式（1－24）中的n和p即为平衡态载流子浓度n0和p0。

（2）间接复合 间接复合是指电子和空穴通过复合中心的复合。由于半导体中晶体结构的不完整性和杂质的存在，在禁带内存在一些深能级，这些能级能俘获自由电子与自由空穴，从而使它们复合，这种深能级称为复合中心。自由载流子通过复合中心复合时也往往会产生光辐射。通常，在自由载流子密度较小时，复合主要是通过复合中心进行的间接复合，而在自由载流子密度较大的情况下，则主要是直接复合。

根据间接复合发生位置的不同，间接复合又可分为体内复合和表面复合。材料表面因加工方式和形状不同而对表面复合有很大影响，如材料表面在研磨、抛光时会出现许多缺陷与损伤，从而产生大量复合中心，使表面载流子复合速度与体内复合速度大不相同。

1.2.4 载流子的运动

半导体中存在能够自由导电的电子和空穴，在外界因素作用下，半导体又会产生非平衡电子和空穴。这些载流子的运动形式有两种：扩散运动和漂移运动。它们都是定向运动，分别与扩散电流和漂移电流相联系。

1.扩散运动

载流子由热运动造成的从高浓度处向低浓度处的迁移运动称为扩散运动。对于杂质均匀分布的半导体，其平衡载流子的浓度分布也是均匀的。因此，不会有平衡载流子的扩散，这时只考虑非平衡载流子的扩散。当然，对于杂质分布不均匀的半导体，需要同时考虑平衡载流子和非平衡载流子的扩散。

图1－9 均匀半导体中载流子的扩散

下面介绍一维稳定扩散的情形。当光均匀地照射一块均匀的半导体时，如图1－9所示，假设光在表面很薄的一层内几乎全部被吸收，而非平衡载流子的产生也局限于这个薄层内。

由图1－9可见，在x＝0处，因光照而产生的非平衡载流子浓度为Δp（0）或Δn（0），由于在x方向存在浓度梯度，光生载流子将沿x方向扩散，最后在半导体内复合而消失。只要入射光保持不变，在x＝0处Δp（0）与Δn（0）也将不变，扩散与复合就不断进行。显然，扩散电流与浓度梯度成正比，即

式中：jn、jp分别为电子和空穴的扩散电流密度；Dn、Dp分别为电子和空穴的扩散系数；负号表示扩散电流的方向与浓度梯度方向相反。

2.漂移运动

载流子在电场的加速作用下，除热运动之外获得的附加运动称为漂移运动。

半导体中晶格原子和杂质离子在晶格点阵位置附近作扩散运动，而载流子则在晶格间作不规则的热运动，并在运动过程中不断与原子和杂质离子发生碰撞，从而改变其运动速度的大小和方向，这种现象称为散射。

由于外加电场的存在，载流子作定向的漂移运动。而由于有散射作用，作漂移运动的载流子在恒定的电场下具有稳定的平均漂移速度。在N型半导体内，漂移所引起的电流密度为

j＝nqv 　（1－27）

式中：j为电流密度；n为载流子密度；q为电子电荷；v为载流子的平均漂移速度。

欧姆定律的微分形式为

j＝σε 　（1－28）

式中：σ为电导率；ε为电场强度。由此可知，有一定值的电场强度，就有一定值的电流密度，因而也就有一定值的平均漂移速度。实际上，载流子密度一般不因电场的存在而改变，只有在特殊情况下，电场强到能改变载流子所处能级或使载流子加速到产生碰撞而电离时，才会引起载流子密度的变化。因此，电场强度与平均漂移速度有如下关系：

v＝με 　（1－29）

式中：μ为迁移率，它表示载流子在单位电场下所取得的漂移速度（cm2／（s·V））。显然，电导率σ与迁移率有如下关系：

σ＝nqμ 　（1－30）

在电场强度ε的作用下，载流子所得到的加速度a为

a＝qε／m＊ 　（1－31）

式中：m＊为载流子的有效质量；q为载流子所带的电荷。载流子在漂移运动中，因为散射作用，在每次碰撞之后漂移速度就下降为零。如果两次碰撞之间的平均自由时间为τf，则τf以后载流子的平均漂移速度v为

将式（1－32）与式（1－29）比较，可得

由此看出，迁移率与载流子的有效质量与平均自由时间τf有关。而电子的有效质量m＊n比空穴的有效质量m＊p小，所以电子的迁移率μn比空穴的迁移率μp大。

3.扩散运动和漂移运动同时存在

在扩散运动和漂移运动同时存在的情况下，载流子的扩散系数与迁移率之间有爱因斯坦关系：

爱因斯坦关系虽然是在平衡情况下得到的，但也适用于非平衡的情况。由式（1－33）可以看出，同一种载流子的扩散系数与迁移率之间存在正比关系，其比例系数是k T／q。它与温度有关，室温下此系数为0.026V。因此，很容易由载流子的迁移率来推算扩散系数。

需要说明的是，虽然电子与空穴均沿x轴方向扩散，但由于它们的扩散系数不同，因此，它们引起的扩散电流不能相互抵消。在无外回路的情况下，这会引起电荷的积累，沿x轴方向产生一个电势差，形成电场，从而阻碍载流子的进一步扩散，直至扩散电流与由此电场产生的漂移电流平衡为止。由于电子的扩散比空穴快，形成的电场方向也将沿x轴方向递减。这种电势差是丹倍于1931年在氧化亚铜中发现的，一般称为丹倍电势。

从以上的分析还可知道，在电场作用下，任何载流子（多数载流子与少数载流子）均要作漂移运动。一般情况下，少数载流子远少于多数载流子，因此漂移电流主要是多数载流子的贡献。然而，在扩散情况下，只有光照所产生的少数载流子存在很大的浓度梯度，所以对扩散电流的贡献主要来自于少数载流子。